数据类型-----集合
一、集合
1.定义:由不同元素组成的集合,集合中是一组无序排列的可hash值,可以作为字典的key;
集合的目的是将不同的值存放到一起,不同的集合间用来做关系运算,无需纠结于集合中单个值。
2.特性:
- 不用元素组成,且元素不重复
- 无序
- 元素不可变(数字、字符串、元组)
3.基本格式:
s = {1,2,3,4,'age'}
print(s) ##输出s
print(type(s)) ##输出s的格式
输出:
{1, 2, 3, 4, 'age'}
<class 'set'>
4.集合的去重功能
s = {1,2,3,3,3,3,3,3,3,3,3}
print(s) ##重复的元素只输出一次
输出:
{1, 2, 3}
5.字符串转集合
s = set('hello') ##使用for循环,并自动去重,且输出无序 print(s)
输出:
{'l', 'o', 'e', 'h'}
二、集合的内置方法
- 添加元素
s = {1,2,'age'}
s.add('1') ##由于这里添加的1是字符串类型,所有不会去重
print(s)
输出:
{1, 2, '1', 'age'}
- 清空元素
s = {1,2,'age'}
s.clear()
print(s) ##输出空的集合
输出:
set()
- 复制集合
s = {1,2,'age'}
l = s.copy()
print(l)
输出:
{'age', 1, 2}
- 删除
s.pop() ##随机删除一个集合中的元素 s.remove('sb') ##删除指定的元素,但是当被删除的元素不存在时会报错 s.discard('sbbb') ##删除指定的元素,当被删除的元素不存在时不会报错
三、集合的关系运算
1.求交集
例: 存在两个列表,python_l = [ 'lcg' , 'szw' , 'zjw' ] linux_l = [ 'lcg' , 'szw' , 'sb' ] ,找出两个列表中共同存在的元素
方法一:使用列表的方法和in方法、for循环
python_l = [ 'lcg' , 'szw' , 'zjw' ] linux_l = [ 'lcg' , 'szw' , 'sb' ] python_and_linux_l = [] for p_name in python_l: if p_name in linux_l: python_and_linux_l.append(p_name) print(python_and_linux_l) ##输出为一个列表 输出: ['lcg', 'szw']
方法二:使用集合的方法
python_l=['lcg','szw','zjw','lcg'] linux_l=['lcg','szw','sb'] p_s=set(python_l) ##将两个列表转换为集合 l_s=set(linux_l) #求交集 print(p_s,l_s) ##分别输出两个集合 print(p_s.intersection(l_s)) ##输出两个集合的交集 print(p_s&l_s) ##输出两个集合的交集(同上),输出为一个集合 输出: {'szw', 'zjw', 'lcg'} {'szw', 'sb', 'lcg'} {'szw', 'lcg'} {'szw', 'lcg'}
2.求并集
python_l=['lcg','szw','zjw','lcg'] linux_l=['lcg','szw','sb'] p_s=set(python_l) l_s=set(linux_l) print(p_s.union(l_s)) ##union和|的效果相同 print(p_s|l_s) 输出: {'szw', 'lcg', 'zjw', 'sb'} {'szw', 'lcg', 'zjw', 'sb'}
3.求差集
python_l=['lcg','szw','zjw','lcg'] linux_l=['lcg','szw','sb'] p_s=set(python_l) l_s=set(linux_l) print('差集',p_s-l_s) ##求p_s中有而l_s中没有的元素 print(p_s.difference(l_s)) ##同上 print('差集',l_s-p_s) ##求l_s中有而p_s中没有的元素 print(l_s.difference(p_s)) ##同上 输出: 差集 {'zjw'} {'zjw'} 差集 {'sb'} {'sb'}
4.交叉补集
python_l=['lcg','szw','zjw','lcg'] linux_l=['lcg','szw','sb'] p_s=set(python_l) l_s=set(linux_l) print('交叉补集',p_s.symmetric_difference(l_s)) print(p_s^l_s) 输出: 交叉补集 {'zjw', 'sb'} {'zjw', 'sb'}
5.求差集并将结果重新赋值给p_s
python_l=['lcg','szw','zjw','lcg'] linux_l=['lcg','szw','sb'] p_s=set(python_l) l_s=set(linux_l) print(p_s,l_s) print('差集',p_s-l_s) print(p_s) p_s.difference_update(l_s) ##相当于p_s=p_s-l_s print(p_s) 输出: {'lcg', 'zjw', 'szw'} {'lcg', 'szw', 'sb'} 差集 {'zjw'} {'lcg', 'zjw', 'szw'} {'zjw'}
四、集合的内置函数
1.判断两个集合是否有交集
s1 = {1,2}
s2 = {3,5}
s3 = {2,6}
print(s1.isdisjoint(s2)) ##不存在交集输出True
print(s1.isdisjoint(s3)) ##存在交集输出False
输出结果:

2.判断一个集合是否是另一个集合的子集
s1 = {1,2}
s2 = {3,5}
s3 = {2}
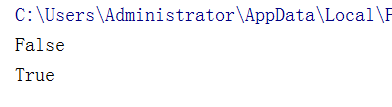
print(s2.issubset(s1)) ##判断的时候是利用for循环将集合中的元素逐个取出再进行比较
print(s3.issubset(s1))
输出结果:
3.判断一个集合是否是另一个集合的父集
s1 = {1,2}
s2 = {3,5}
s3 = {2}
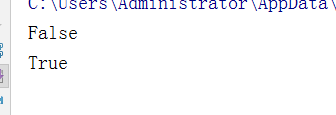
print(s1.issuperset(s2))
print(s1.issuperset(s3))
输出结果:
4.对集合进行更新
s1 = {1,2,'lee','123ds'}
s2 = {3,5}
print(s1.union(s2)) ##只是求并集,并没有对s1重新赋值
print(s1)
s1.update(s2)
print(s1.update(s2)) ##对s1进行了重新赋值,与 s1 = s1.union(s2) 效果相同
print(s1)
输出结果:

五、补充
1.定义不可变集合(普通集合可以增加or删除元素)
s1 = frozenset('hello') ##只能通过将可迭代对象转换为不可变集合 s2 = frozenset(['hello',1,2,'12s']) print(s1) ##生成的不可变集合和普通的格式也不同,会在集合外加上frozenset() print(s2)
输出结果:

2.可迭代对象去重的快捷方法—>将可迭代对象转换为集合后再转换回来
li = [1,2,3,'1w','1w',1,2] ##集合不能使用索引但是可以使用for循环进行遍历 l =list(set(li)) print(l)
输出:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号