Pow(x, n)

Power(x,n)

解题思路

思路一：for循环迭代。

代码比较简单，就不贴出来了。结果很显然超时。

思路二：快速幂

代码超时之后猛然想起来之前学过一招制敌的方法，但是一时想不起来名字。只好百度
快速幂算法的思想可以总结为下面的数学公式

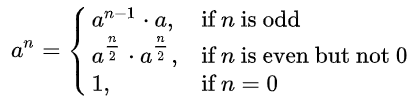
思路比较简单，其实是二分的思路。但是如果之前没有相应的思维训练，不可能一下子想出来的。

class Solution {
    public double myPow(double x, int n) {
        if(n == 0){
            return 1.0;
        }
        if(n < 0){ //加入负数特殊判断。
            return 1.0/myPow(x,Math.abs(n+1))/x; //n+1的目的是防止负数取绝对值时候溢出[-2^31,2^31 - 1]，自然x需要提出来
        }
        if((n&1) == 1){//奇数
            return x * myPow(x,n-1);
        }else{
            double num = myPow(x,n/2);
            return num * num;
        }
    }
}

• 时间复杂度：O(logn),即为递归的层数
• 空间复杂度：O(logn),即为递归的层数。这是由于递归的函数会使用栈空间。

思路三：利用二进制的方式进行正向迭代

代码如下：

class Solution {
    public double myPow(double x, int n) {
        long N = n;
        return N < 0?1.0/quickMi(x,-N):quickMi(x,N);
    }
    public double quickMi(double x,long N){
        int ex = 1;
        double ans = 1.0;
        while(N > 0){
            //System.out.println("ex = " + ex);
            if((N&1) == 1){
                ans = ans * x;
            }
            N = N >> 1; //右移，除2
            x = x * x;//(x^1 * x^2 * x^4 * x^8)
        }
        return ans;
    }
}

• 时间复杂度：O(logn),即对n进行二进制拆分的时间复杂度
• 空间复杂度：O(1)，常数级别的