总结一下排列组合的算法问题

什么是全排列？

全排列（Full Permutation）。一般把1到n这n个整数按照某个顺序摆放的结果称为这n个数的一个排列，而全排列指这n个整数能形成的所有排列。

例如对1、2、3这三个整数来说

（1，2，3），（1，3，2），（2，1，3），（2，3，1），（3，1，2），（3，2，1）就是一个全排列。

　　那么如何解决这类全排列问题？，从递归的角度去考虑，如果把问题描述成“输出1到n个整数的全排列”，那么它就可以被分为若干个子问题：

“输出以1开头的全排列”“输出以2为开头的全排列”……“输出以n为开头的全排列”。不妨设定一个数组P，用来存放当前的排列；再设定一

个散列数组hashTable，其中hashTable[x]当整数x已经在数组P中时为true。（毕竟全排列中的一个排列每一项只用一次）。

　　现在按顺序往P的第一位到第n位中填入数字。不妨假设当前已经填好了P[1]到P[index-1]，正准备填P[index]。显然需要枚举1到n，如果

当前数字x还没有在P[1]到P[index-1]中（即hashTable[x]==false）,那么就把它填入P[index]，同时将hashTable[x]置为true，然后去处理第

index+1位（即进行递归）；而当递归完成时，再将hashTable[x]还原位false,以便让P[index]填下一个数字。

 

我简单的画了一下数组图，如下：

 

 

 代码如下：

#include <stdio.h>


void generateP(int index);  

const int maxn = 11;

int n;
int P[maxn],hashTable[maxn]={0};
int main(){
    
    int array[3] = {1,2,3};
    
    n = 3;
    
    //从当前处理排列的第0号开始 
    generateP(1); 
    return 0;
} 


void generateP(int index){
    
    if(index == n+1){
        for(int i = 1;i<=n;i++){
            printf("%d ",P[i]);
        }
        printf("\n");
        //return;
    } 
    
    //递归体
    for(int x = 1;x <=n;x++){//枚举1到n，试图将x填入P[index] 
        if(hashTable[x]==0){//如果x不在P[0]到P[index-1]中
            P[index] = x;    //令P的第index位为x，即把x加入当前排列 
            hashTable[x] = 1; //记录x已经在P中了（不能再利用） 
            generateP(index+1);    //处理排列的第index+1号位
            hashTable[x] = 0;     //已经处理完P[index]为x的子问题了，还原状态 
        }
    } 
}

可以看到输出结果如下：

 

 

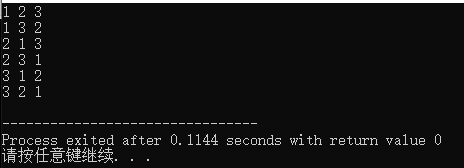
这个和我们之前的思路是一致的。即从递归的角度去考虑，“输出以1开头的全排列”、“输出以2开头的全排列”、“输出以3开头的全排列”。

另一种写法

 

 

#include <stdio.h>




void swap(int A[],int i,int j);
void printArray(int A[],int n);
void perm(int A[],int p,int q);

int main(){
    
    int A[3] = {1,2,3};
    perm(A,0,3);
    
    return 0;
}

void swap(int A[],int i,int j){
    int temp = A[i];
    A[i] = A[j];
    A[j] = temp;
}

void printArray(int A[],int n){
    for(int i = 0;i < n;i++){
        printf("%d ",A[i]);
    }
    printf("\n");
}

void perm(int A[],int p,int q){
    if(p == q){
        printArray(A,q);
    }
    
    for(int i = p;i <q;i++){
        swap(A,p,i);
        perm(A,p+1,q);
        swap(A,p,i);  
    }
}