十六周作业

1-1 If a directed graph G=(V, E) is weakly connected, then there must be at least |V| edges in G.

F

at least |V-1|

1-2 邻接矩阵作为有向图的存储结构，则某顶点的度就是该顶点所在列的非零元素的个数。

F

出度看行，入度看列，度是行加列

1-3 用邻接表法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关

F

捉虫，邻接矩阵只与结点个数有关，邻接表与结点和边都有关

2-1 图G如下，从A开始深度优先遍历该图，不可能的遍历序列是（      ）。

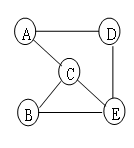
ACDEB

2-2 通过对无向图进行先深搜索，可以判断该图是否是连通图，或找出图的连通分量及先深生成树。

对

深度优先遍历(Depth First Search)的主要思想是首先以一个未被访问过的顶点作为起始顶点，沿当前顶点的边走到未访问过的顶点。当没有未访问过的顶点时，则回到上一个顶点，继续试探别的顶点，直至所有的顶点都被访问过。

无向图 G 的一个极大连通子图称为 G 的一个连通分量（或连通分支）。连通图只有一个连通分量，即其自身；非连通的无向图有多个连通分量。连通分量与连通分量之间没有任何边相连。深度优先遍历可以用来求连通分量。

由深度优先搜索得到的树为深度优先生成树。

深度优先生成树和广度优先生成树 (biancheng.net)

深度优先遍历与连通分量 | 菜鸟教程 (runoob.com)

2-3 用邻接表表示图进行广度优先遍历时，通常借助（ ）来实现算法

广度优先借助队列，深度优先借助栈

数据结构之图的遍历：深度优先遍历（DFS）_调用两次深度优先遍历算法才完成了-CSDN博客

算法：深度优先遍历和广度优先遍历_广度优先遍历和深度优先遍历-CSDN博客

2-4 

已知图的邻接表如下图所示，则从顶点v1出发广度优先遍历的结果是（ ）。

v1v0v2v3

v1->0-->v0;v0->1-->;v0->2-->v2;v0->3-->v3

7-1 

以邻接矩阵作存储结构，编写程序对给定的无向图（图中包含n个顶点，编号为0至n-1）进行深度优先遍历，并在遍历的过程中计算图G的连通分量个数及边的数目。

本题限定在遍历过程中，如果同时出现多个待访问的顶点，则优先选择编号最小的一个进行访问，以顶点0为遍历起点。

邻接矩阵的类型描述

#define  MaxVexNum   20     //最大顶点数目
typedef struct 
{    int  arcs[MaxVexNum][MaxVexNum];
     int  vexnum, arcnum;
}AMGraph;

输入格式:

第一行输入图的顶点数和边数。

接下来每行代表一条边，输入边依附的两个顶点的编号。各边输入先后次序无要求。

输出格式

输出分三行

• 第一行 深度优先遍历序列。序列中每个顶点编号后跟一个空格。
• 第二行 连通分量个数
• 第三行 边数

对于下面给出的无向图G

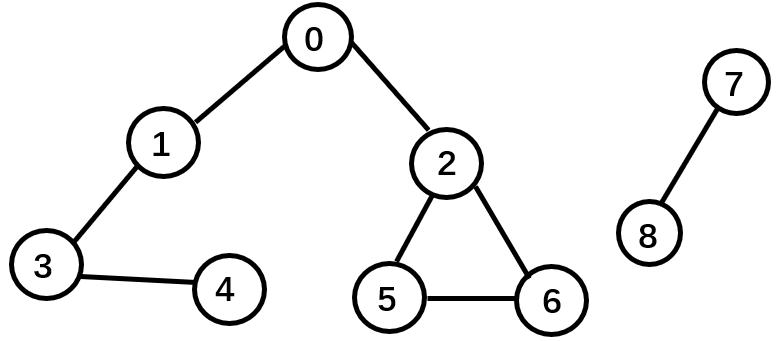
输入样例:

9 8
0 1
0 2
1 3
3 4
2 5
2 6
5 6
7 8

输出样例:

0 1 3 4 2 5 6 7 8 
2
8

代码:

#include <iostream>
using namespace std;
#define mvnum 20
typedef struct {
    int arcs[mvnum][mvnum];
    int vnum, arcnum;
}amggragh;

bool visited[mvnum]; //访问标志数组, 其初始值为false

void dfs(amggragh g,int v) {
    cout << v<<" ";//输出该点
    visited[v] = true;//标记为已访问
    for (int i = 0; i < g.vnum; i++) {
        if (g.arcs[v][i]==1 && visited[i] == 0) {//遍历邻接点，如果和邻接点有边，且未被访问
            dfs(g, i);//递归访问该邻接点
        }
    }
}
void dfs_d(amggragh g) {//深度优先搜索操作
    int i;
    int cnt = 0;//连通图计数
    for (i = 0; i < g.vnum; i++) {
        if (visited[i] == 0) {//遍历所有点，如果该点未被访问
            dfs(g, i);
            cnt++;
        }
    }
    cout << endl;
    cout << cnt;
}
int main()
{
    amggragh g;
    int v1, v2;
    cin >> g.vnum >> g.arcnum;
    for (int i = 0; i < g.arcnum; i++) {
        cin >> v1 >> v2;
        g.arcs[v1][v2] = 1;//该边存在
    }
    dfs_d(g);
    cout << endl;
    cout << g.arcnum;

}

 

7-2

农夫知道一头牛的位置，想要抓住它。农夫和牛都位于数轴上，农夫起始位于点N(0<=N<=100000)，牛位于点K(0<=K<=100000)。农夫有两种移动方式：

1、从X移动到X-1或X+1，每次移动花费一分钟
2、从X移动到2*X，每次移动花费一分钟

假设牛没有意识到农夫的行动，站在原地不动。农夫最少要花多少时间才能抓住牛？

输入格式:

两个整数，N和K

输出格式:

一个整数，农夫抓到牛所要花费的最小分钟数

输入样例:

在这里给出一组输入。例如：

5 17

输出样例:

在这里给出相应的输出。例如：

4

代码:

#include <iostream>
#include<queue>
#define maxn 100001
using namespace std;
int d[3];
bool visited[maxn] ;
int res[maxn];
void bfs(int vs, int ve) {//起点和终点
    queue<int> q;
    int vn;
    q.push(vs);
    visited[vs] = 1;
    while (!q.empty()) {//队列不为空q.empty()为空，返回值为1
        vn = q.front();//取出队列的头，和ve作比较
        q.pop();
        if (vn == ve)
            break;
        d[0] = vn - 1;
        d[1] = vn + 1;
        d[2] = vn * 2;
        for (int i = 0; i < 3; i++) {
            if (d[i] >= 0 && d[i] < maxn && visited[d[i]] == 0) {//注意条件！！一开始第一个条件没有写成大于等于。。。
                q.push(d[i]);
                visited[d[i]] =1;
                res[d[i]] = res[vn] + 1;
            }
        }
    }
    cout << res[ve];
}
int main()
{
    int n, k;
    cin >> n >> k;
    bfs(n, k);
}