CodeForces 708C Centroids|换根DP

题目链接
第三道换根Dp?
题目大意：
（直接抄luogu的）
给定一颗树，你有一次机会，删去一条边，再加入一条边，保证改造后还是一棵树。问第 \(i\) 个点能否可以通过改造，成为这颗树的重心？（如果以某个点为根，每个子树的大小都不大于 \(\frac{n}{2}\)，则称某个点为重心）
\(2\le n\le 400000\)

思路：
考虑假如有大于 \(\frac n2\) 的子树，我们可以通过将该子树的最大合法子树（指不大于 \(\frac n2\) 的子树）接到根上来尽量使其合法。
先将范围缩小至一个点，那么我们可以通过dp得出每个子树的大小（下文用 \(siz\) 表示）和最大子树（用 \(ma\) 表示）以及最大合法子树的大小（下文用 \(mx\) 表示）。若 \(siz[root]-mx[siz[root]]\le \frac n2\) 则该点可为重心。这里复杂度是\(O(n)\)的。

考虑扩展至 \(n\) 个点，显然不能重复上述算法 \(n\) 次，考虑使用换根Dp，那么我们需要考虑上述的三个数据的维护。\(siz_x\)就是\(max(siz_x,n-siz_x)\)，这很好理解。我们可以通过直接分类讨论的方式忽略 \(ma\) 和 \(mx\) 的维护。
易知原本子树的部分无需改动，需要维护的是 \(n-siz_x\) 部分的最大合法子树。设原来的的根为 \(rot\)，有一种可能是把 \(n-siz_rot\) "连根拔起"。也可能是若 \(mx_{rot}\)不在现在的根内，则取 \(mx\)，否则 取第二大的合法子树大小，这个需要在执行换根Dp前维护好。
上面的话有点难理解，这里上幅图

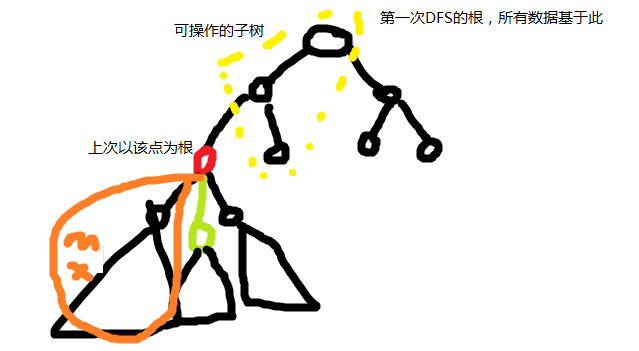
换根的同时，我们对每个点进行判断，割掉最大子树的最大合法子树后全部子树均小于等于 \(\frac n2\) 即可作为重心。

上代码

#include<bits/stdc++.h>
#define N 400100
using namespace std;
int cc,to[2*N],net[2*N],fr[N],siz[N],mx1[N],mx2[N],ma[N],ans[N];
int n,u,v;bool vis[N];
void addedge(int u,int v)
{
	cc++;
	to[cc]=v;net[cc]=fr[u];fr[u]=cc;
}
void dfs(int x)
{
	siz[x]=1;
	for (int i=fr[x];i;i=net[i])
	{
		if (siz[to[i]]) continue;
		dfs(to[i]);
		siz[x]+=siz[to[i]];
		if (siz[ma[x]]<siz[to[i]]) ma[x]=to[i];
		if (siz[to[i]]<=n/2)
		{
			if (siz[to[i]]>siz[mx1[x]]) 
			{
				mx2[x]=mx1[x];
				mx1[x]=to[i];
			}
			else
			if (siz[to[i]]>siz[mx2[x]])
				mx2[x]=to[i];
		}
		else
		{
			if (siz[mx1[to[i]]]>siz[mx1[x]]) 
			{
				mx2[x]=mx1[x];
				mx1[x]=mx1[to[i]];
			}
			else
			if (siz[mx1[to[i]]]>siz[mx2[x]])
				mx2[x]=mx1[to[i]];
	}
	}
}//第一次处理
void CR(int x,int maxx,int max1)
{
	vis[x]=true;
	if (siz[ma[x]]<=n/2)
	{
		if (n-siz[x]>n/2)
		{
			if (n-siz[x]-maxx>n/2&&n-siz[x]-siz[max1]>n/2) 
			ans[x]=0;else ans[x]=1;
		}
		else ans[x]=1;
	}
	else if (siz[ma[x]]-siz[mx1[ma[x]]]<=n/2) ans[x]=1;else ans[x]=0;
	for (int i=fr[x];i;i=net[i])
	{
		if (vis[to[i]]) continue;
		int ot=(n-siz[x])*(int(bool(n-siz[x]<=n/2)));
		if (to[i]==mx1[x])
		{ 
			if (max1==to[i]) max1=0;
			if (siz[mx2[x]]>=siz[max1])
				CR(to[i],max(maxx,ot),mx2[x]);
			else
				CR(to[i],max(maxx,ot),max1);
		}
		else 
		{
			if (max1==to[i]) max1=0;
			if (siz[mx1[x]]>=siz[max1])
				CR(to[i],max(maxx,ot),mx1[x]);
			else
				CR(to[i],max(maxx,ot),max1);
		}
	}
}//换根
int main()
{
	scanf("%d",&n);
	for (int i=1;i<n;i++)
	{
		scanf("%d%d",&u,&v);
		addedge(u,v);
		addedge(v,u);
	}
	dfs(1);
	CR(1,0,0);
	for (int i=1;i<=n;i++) cout<<ans[i]<<" ";
	return 0;
}