【学习笔记】线段树
UPDATE 20190926 更新对线段树本质的理解
搬运自自己一年前的文章(
\(Part -1\) 约定
\(Part 0\) 介绍
线段树(\(Segment\) \(Tree\))是一种用来处理区间问题的数据结构。这棵二叉树功能非常强大,支持的有
- 区间修改,区间查询
- 区间修改,单点查询
- 单点修改,区间查询
单点修改,单点查询(用数组就行啊)
-----分割线----
线段树的本质是什么?
大概就是一个可以支持信息合并,以分治(亦有人说是分块,这里看个人理解)为思想的数据结构。与树状数组的区别是可以不满足可减性
举个例子,区间最大值可以用线段树维护,因为一个区间的最大值可以由直接由下面的得出。
而连续最大和呢?不能由下面的直接得出,所以不能直接维护。当然,间接维护还是支持的。
-----分割线----
比如说有一个长度为N的数列,有2类操作:
1、将某个区间中的数都加上\(x\)。
2、询问某个区间中所有数的和并输出。
数据范围:
\(0 \le N \le 100000\)
\(0 \le M \le 100000\)
(N,数列个数,M,操作数)
上面这一道题就是线段树的模板,毫无疑问,如果暴力搞,时间复杂度是\(O(NM)\)的,承受不了,但是如果使用线段树的话就可以在\(O(MlogN)\)的时间内解决这道题。那么接下来我们就来讲一讲线段树究竟是如何构造与实现的。
\(Part 1\) 入门
\(Part 1.1\) 建树
首先观察这颗线段树
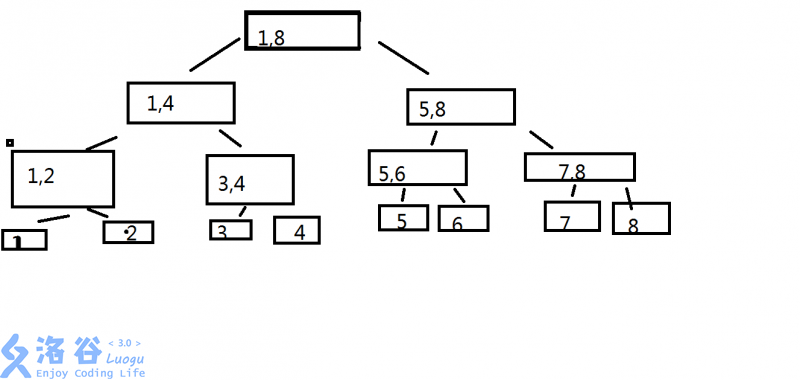
可以看出:
1.这颗树的每一个非叶节点的点,都有两个儿子。
2.设该节点(非叶节点)表示\([l,r]\)的信息,则左儿子表示\([l,mid]\)的信息,右儿子表示\([mid+1,r]\)的信息。
**3.叶结点表示单独一个节点的信息
**
回归正题,我们怎么建树呢?
(对于普通线段树,设该节点的位置为\(x\),则左儿子的位置为\(2x\),右儿子的位置为\(2x+1\)。)
我们可以通过递归建树,当建到叶结点时赋值并返回,在返回时,我们可以顺便求出其他节点的信息了。
代码
void maketree(long long t,long long l,long long r)
{
if (l==r) {tree[t]=a[l];return ;}//叶结点
long long mid=(l+r)/2;
maketree(t*2,l,mid);maketree(t*2+1,mid+1,r);//递归左儿子和右儿子
tree[t]=tree[t*2]+tree[t*2+1];//求和
}
\(Part 1.2\) 单点操作
首先,思考一下,上图中若要更新一个位置(叶结点)的信息,哪些地方需要更新?
若要更改5号节点,更新的位置如下(橙色代表更新)
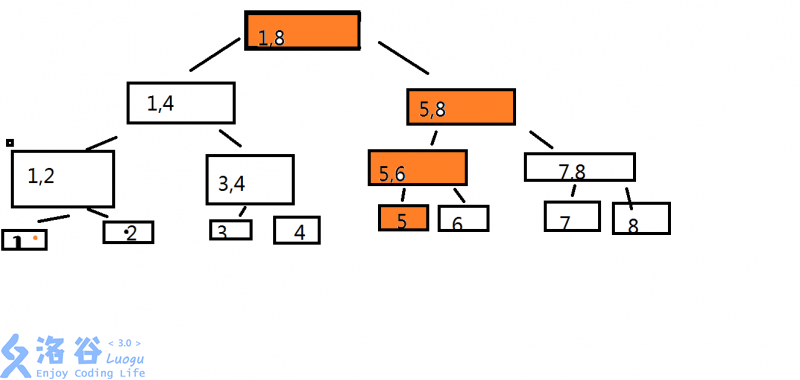
可以看出,这其实就像一条链,所以,我们就可以逐层丢锅递归下去,然后再逐层递归上来更新信息。就完成了线段树的单点修改
代码如下
//此程序以求最大值为例
void update(int t,int l,int r,int x,int y)
{
if (l==x&&r==x) {tree[t]=y;return ;} //到叶结点时直接修改
int mid=(l+r)/2;
if (x<=mid) update(t*2,l,mid,x,y);
else update(t*2+1,mid+1,r,x,y);
tree[t]=max(tree[t*2],tree[t*2+1]);//更新非叶节点信息
}
那如何单点查询呢?
其实和单点修改一样,我们逐层往下递归就能找到答案了。
代码和单点修改差不多,只需删掉更新部分,增加返回部分(\(return\))就可以了。
\(Part 2\) 提高
看完上面这些,恭喜你,可以写一个粗拙的线段树了,然而,这些解决上面的题还不够用,所以接着往下看吧
\(Part 2.1\) 区间更新
区间更新其实可以暴力改成单点更新。然而,你可能发现,目前为止,只有叶节点有用。那么,区间更新就需要用到其他节点了。
想象一下,当你要传达通知到1,2,3那儿,而刚好,他们在同一个公司。而且公司只有那三个人,那我们就可以直接传到公司了。感觉不是一般的懒!
而当我们进行区间更新时,我们可能发现某些节点的所有子节点都在更新范围,那么此时我们可以先在那一个节点打一个标记,等到用到时才往下进行更新,这就是lazy标记。
代码
void add(long long t,long long l,long long r,long long al,long long ar,long long c)
{
if (l==al&&r==ar) {addnote(t,l,r,c);return ;}//添加lazy标记
free(t,l,r);//下放lazy标记
long long mid=(l+r)/2;
if (ar<=mid) add(t*2,l,mid,al,ar,c);else
if (al>mid) add(t*2+1,mid+1,r,al,ar,c);else
{
add(t*2,l,mid,al,mid,c);
add(t*2+1,mid+1,r,mid+1,ar,c);
}
tree[t]=tree[t*2]+tree[t*2+1];//更新信息
}
请想一想,addnote函数中需要添加什么?为什么?
void addnote(long long t,long long l,long long r,long long c)
{
tree[t]+=(r-l+1)*c;
lazy[t]+=c;
}
\(Part 2.2\) 区间更新
我们可以把各个查询节点的信息进行整合,即可得出答案。当然,我们不必每次都下到叶节点,可以通过其他节点
(即:某些所有子节点都在查询范围的节点)的信息得出。
需要注意的是,无论是更新还是查询,我们都需要进行释放lazy标记的操作,防止出现错误。释放lazy标记,就是把当前节点的标价删去,把原标记下放至此节点的子节点。
//释放懒标记
void free(long long t,long long l,long long r)
{
long long mid=(l+r)/2;
addnote(t*2,l,mid,lazy[t]);
addnote(t*2+1,mid+1,r,lazy[t]);
lazy[t]=0;
}
//查询(求和)
long long ask(long long t,long long l,long long r,long long al,long long ar)
{
if (l==al&&r==ar) return tree[t];
free(t,l,r);
long long mid=(l+r)/2;
if (ar<=mid)
return ask(t*2,l,mid,al,ar);else
if (al>mid)
return ask(t*2+1,mid+1,r,al,ar);//如果在范围只覆盖一个儿子,则直接递归
else
{
return ask(t*2,l,mid,al,mid)+ask(t*2+1,mid+1,r,mid+1,ar);//否则分别求出后进行信息整合
}
}
\(Part 3\) 一些小事情
- 线段树大小应开大一些(约\(4n\))!
- 记得释放lazy标记!
\(Part 4\) 结束
最终线段树就是这样啦:
#include<bits/stdc++.h>
using namespace std;
long long tree[400400],lazy[800800],a[100100];
long long n,m,cz,l,r,c;
void maketree(long long t,long long l,long long r)
{
if (l==r) {tree[t]=a[l];return ;}
long long mid=(l+r)/2;
maketree(t*2,l,mid);maketree(t*2+1,mid+1,r);
tree[t]=tree[t*2]+tree[t*2+1];
}
void addnote(long long t,long long l,long long r,long long c)
{
tree[t]+=(r-l+1)*c;
lazy[t]+=c;
}
void free(long long t,long long l,long long r)
{
long long mid=(l+r)/2;
addnote(t*2,l,mid,lazy[t]);
addnote(t*2+1,mid+1,r,lazy[t]);
lazy[t]=0;
}
void add(long long t,long long l,long long r,long long al,long long ar,long long c)
{
if (l==al&&r==ar) {addnote(t,l,r,c);return ;}
free(t,l,r);
long long mid=(l+r)/2;
if (ar<=mid) add(t*2,l,mid,al,ar,c);else
if (al>mid) add(t*2+1,mid+1,r,al,ar,c);else
{
add(t*2,l,mid,al,mid,c);
add(t*2+1,mid+1,r,mid+1,ar,c);
}
tree[t]=tree[t*2]+tree[t*2+1];
}
long long ask(long long t,long long l,long long r,long long al,long long ar)
{
if (l==al&&r==ar) return tree[t];
free(t,l,r);
long long mid=(l+r)/2;
if (ar<=mid)
return ask(t*2,l,mid,al,ar);else
if (al>mid)
return ask(t*2+1,mid+1,r,al,ar);
else
{
return ask(t*2,l,mid,al,mid)+ask(t*2+1,mid+1,r,mid+1,ar);
}
}
int main()
{
cin>>n>>m;
for (long long i=1;i<=n;i++)
cin>>a[i];
maketree(1,1,n);
for (long long i=1;i<=m;i++)
{
cin>>cz;
if (cz==1)
{
cin>>l>>r>>c;
add(1,1,n,l,r,c);
}
else
{
cin>>l>>r;
cout<<ask(1,1,n,l,r)<<endl;
}
}
return 0;
}
如果有兴♂趣,可以试着做一下3373
本文中部分内容来源于网络,侵删。
参考资料
【1】(https://www.cnblogs.com/wozaixuexi/p/9084534.html)
【2】
(https://pks-loving.blog.luogu.org/senior-data-structure-qian-tan-xian-duan-shu-segment-tree)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号