【学习笔记】后缀数组(1)
后缀数组学习笔记(1)
全文1820词,预计阅读时间5min
前言
后缀数组是处理字符串的有力工具,常在比赛中用到。本文主要介绍后缀数组的概念与部分例题。
关于部分例题,我们将在后续文章介绍。
定义
-
原串:本文约定用\(t\)或\(st\)表示
-
字符串比较:对于两个字符串\(x\),\(y\)
对于\(1\le i\le min(len_x,len_y)\),若\(x_i \neq y_i\),则当前字符小的那个字符串小
如果到字符串末都比较不出结果,则长度长的字符串大
(其实就是字典序)
(如果两个字符串相同,先出现的排前面)
-
\(SA_i\):第\(i\)大的后缀的开始位置
-
\(rank_i\):字符串中,后缀开始位置为\(i\)的的排名(可重复)
\(SA\)与\(rank\)是逆运算
-
\(LCP\):即最长公共前缀
从排序说起
-
基数排序
对于一个有两个关键字的序列,我们要使其有序(先按第一关键字大小,如果相同,再按第二关键字大小排序)。
那么,我们可以先按第二关键字排序,此时序列是按照第二关键字从小到大排列的。我们再从左到右,按第一关键字排序。这样就可以使得其有序。这就是基数排序,基数排序是稳定的。
举个栗子:
(1,6)(1,5)(2,3)(3,4)(8,5)(16,43)(2,20)(4,28)
按第二关键字排序后
(2,3)(3,4)(1,5)(8,5)(1,6)(2,20)(4,28)(16,43)
按第一关键字排序后
(1,5)(1,6)(2,3)(2,20)(3,4)(4,28)(8,5)(16,43)
此时序列有序
-
排名
我们可以使用以下代码段来求排名
//排名从0开始编号 for (int i=0;i<=maxg;i++) sum[i]=0; for (int i=n-1;i>=0;i--) sum[rank[i]]++; for (int i=1;i<maxg;i++) sum[i]+=sum[i-1];//前缀和,意义是小于等于此数的有多少 for (int i=n;i>0;i--)//后出现的名次大 sa[--sum[rank[i]]]=i;请自行思考此程序段的正确性。
构造后缀数组
关于后缀数组的构造,有倍增与\(DC3\)两种算法。倍增算法较为简单,本文主要介绍倍增算法。
注:倍增算法\(O(nlogn)\),\(DC3\)算法\(O(n)\),\(n\)为字符串长度
我们可以对从每个字符开始,长度为\(2^i\)的字符串进行排序(当字符串长度不足时,根据上文定义,在后面补比所有出现过字符还要小的字符)。当到达\(len_t\le 2^i\),显然所有字符串的排名会变得不重复。并且当长度为\(2^i\)的字符串排名不重复时,长度为\(2^{i+1}\)的字符串排名也不重复。
当我们知道长度为\(2^i\)的排名时,如何求出长度为\(2^{i+1}\)的排名呢?我们知道\(2 \times 2^i=2^{i+1}\),与上文的基数排序对比,想出怎么做了吗?
其实,我们可以直接用\(2^i\)的排名搞。如下图所示,以前半段的排名为第一关键字,以后半段的排名作为第二关键字,做基数排序,就可以知道新的排名了。
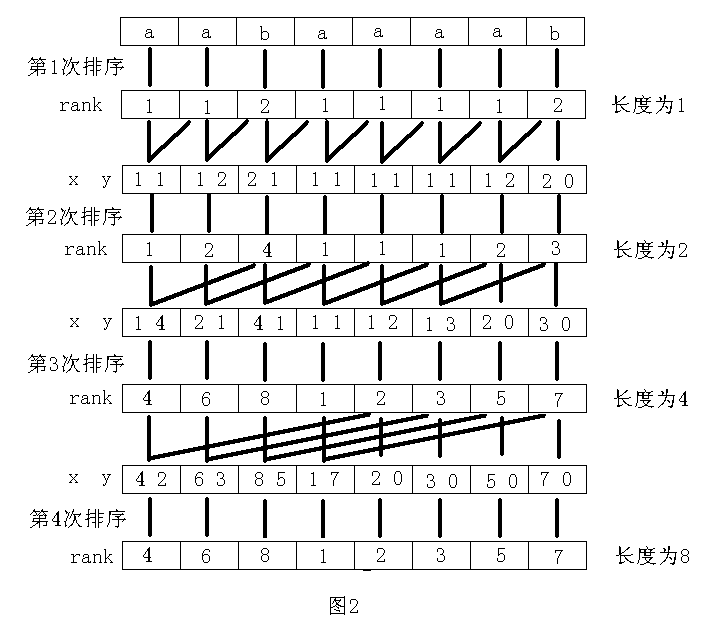
所以,我们只用在字符串中求出长度为\(2^0=1\)的排名,后面的排名都可以通过基数排序求出。
我们的程序基本成形了,步骤如下:
1.求出长度为\(2^0\)的排名
2.基数排序,由\(2^i\)的排名求出\(2^{i+1}\)的排名
3.处理每个后缀的排名
不过这里还要介绍一个优化:第二关键字其实不用排序,我们可以通过以下方法得出顺序:
设长度为\(2^i\)
1.长度不到\(2^i\)的字符串,按从长到短的顺序加入数组
2.从前往后遍历\(SA\),若\(SA_i-2^i \ge 0\)(字符串从0开始),则将其加入数组
此数组即为第二关键字的排序。
上代码(luogu3809)
本题就是求最终的\(SA\)数组,处理完输出即可。当然,本题中可以把基数排序换成快排。
#include<bits/stdc++.h>
using namespace std;
int rank[1000100],nrank[1000100],sa[1000100],sum[1000100],ans[1000100],n,p[1000100];
string st;
bool the_same(int x,int y,int l)
{
if (rank[x]!=rank[y]) return false;
if ((x+l>=n&&y+l<n) || (x+l<n&&y+l>=n))return false;
if (x+l>=n&&y+l>=n) return true;
return rank[x+l]==rank[y+l];
}
int main()
{
cin>>st;
n=st.size();
int maxg=max(128,n);
for (int i=0;i<n;i++)
sum[rank[i]=int(st[i])]++;
for (int i=1;i<=128;i++)
sum[i]+=sum[i-1];
for (int i=n-1;i>=0;i--)
sa[--sum[rank[i]]]=i;
for (int l=1;l<n;l<<=1)
{
int k=0;
for (int i=n-l;i<n;i++) p[++k]=i;
for (int i=0;i<n;i++)
if (sa[i]-l>=0) p[++k]=sa[i]-l;//第二关键字排序
for (int i=0;i<=maxg;i++) sum[i]=0;
for (int i=n-1;i>=0;i--)
sum[rank[i]]++;
for (int i=1;i<maxg;i++)
sum[i]+=sum[i-1];
for (int i=n;i>0;i--)
sa[--sum[rank[p[i]]]]=p[i];
nrank[sa[0]]=0;
int ns=0;
for (int i=1;i<n;i++)
{
if (!the_same(sa[i],sa[i-1],l))
{
nrank[sa[i]]=++ns;
}
else
{
nrank[sa[i]]=ns;
}
}
for (int i=0;i<n;i++)
{
rank[i]=nrank[i];
nrank[i]=0;
}
if (ns==n-1) break;
}
for (int i=0;i<n;i++)
cout<<sa[i]+1<<" ";
return 0;
}
Height数组
有了\(rank\)与\(sa\)数组,我们可以做的事还不多,那么我们现在引入一个新数组\(height\),其意义是排名相邻的两个后缀的\(LCP\)的长度,显然,一个个求会TLE。如何优化呢?
我们现在引入一些东西:
-
对于两个字符串,其\(LCP\)长度为它们中间的所有\(height\)的最小值(易证)
-
定义\(h\)数组为某一个后缀与排名前一位的后缀的\(LCP\)的长度
关于\(h\)(\(height\))数组的一个性质
\(\huge h_i \ge h_{i-1}-1 (height_{rank_i} \ge height_{rank_{i-1}}-1\)
证明:
定义\(j\)是开头为\(sa_{rank_{i}-1}\)的字符串,其\(LCP\)为\(h_i\)。
那么以\(j+1\)与\(i\)的\(LCP\)显然是\(h_i-1\)
由上面的定理,得\(j+1\)至\(i\)中间的\(height\)值大于等于\(h_i-1\)。
显然,\(rank_i>rank_{j+1}\),且\(sa_{rank_i-1}\)在\(j+1\)到\(i-1\)之间。
证毕。
所以,\(height_{rank_i} \ge height_{rank_{i-1}} -1\)
所以,我们可以按照\(rank\)顺序,求出\(height\),时间复杂度降为\(O(N)\)
代码如下
void calc_height()
{
int j=0;
for (int i=0;i<n;i++)
{
if (j) j--;
if (!rank[i])
{
j=0;
continue;
}
for (int k=sa[rank[i]]+j,l=sa[rank[i]-1]+j;;)
{
if (st[k]==st[l]) j++,k++,l++;else break;
}
height[rank[i]]=j;
}
}
例题
Luogu 2408 不同子串个数
(SPOJ 694 / 705)
题目链接 题意:给出一个字符串,求不同子串的个数
题解:一个子串一定是一个后缀的前缀,所以我们求出子串个数后,再减去相同子串个数,即每个后缀与排名是其前一位的后缀的\(LCP\),即为答案。
由于篇幅关系,剩余题目本文不再给出,请移步至下方链接阅读
参考资料:
[1] 罗穗骞,IOI2009 国家集训队论文《后缀数组——处理字符串的有力工具》2009.1



