二叉树常用操作

原文：https://www.cnblogs.com/willwu/p/6007555.html

树的介绍

1. 树的定义

树是一种数据结构，它是由n（n>=1）个有限节点组成一个具有层次关系的集合。

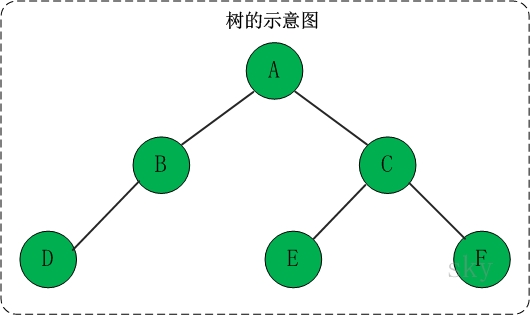
把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
(01) 每个节点有零个或多个子节点；
(02) 没有父节点的节点称为根节点；
(03) 每一个非根节点有且只有一个父节点；
(04) 除了根节点外，每个子节点可以分为多个不相交的子树。

 

2. 树的基本术语

若一个结点有子树，那么该结点称为子树根的"双亲"，子树的根是该结点的"孩子"。有相同双亲的结点互为"兄弟"。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。

结点的度：结点拥有的子树的数目。
叶子：度为零的结点。
分支结点：度不为零的结点。
树的度：树中结点的最大的度。

层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1。
树的高度：树中结点的最大层次。
无序树：如果树中结点的各子树之间的次序是不重要的，可以交换位置。
有序树：如果树中结点的各子树之间的次序是重要的, 不可以交换位置。
森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。

 

二叉树的介绍

1. 二叉树的定义

二叉树是每个节点最多有两个子树的树结构。它有五种基本形态：二叉树可以是空集；根可以有空的左子树或右子树；或者左、右子树皆为空。

2. 二叉树的性质

二叉树有以下几个性质：TODO(上标和下标)
性质1：二叉树第i层上的结点数目最多为 2^{i-1} (i≥1)。
性质2：深度为k的二叉树至多有2^{k}-1个结点(k≥1)。
性质3：包含n个结点的二叉树的高度至少为log₂ (n+1)。
性质4：在任意一棵二叉树中，若终端结点的个数为n₀，度为2的结点数为n₂，则n₀=n₂+1。

 

2.1 性质1：二叉树第i层上的结点数目最多为 2^{i-1} (i≥1)

证明：下面用"数学归纳法"进行证明。
        (01) 当i=1时，第i层的节点数目为2^{i-1}=2^{0}=1。因为第1层上只有一个根结点，所以命题成立。
        (02) 假设当i>1，第i层的节点数目为2^{i-1}。这个是根据(01)推断出来的！
               下面根据这个假设，推断出"第(i+1)层的节点数目为2^{i}"即可。
                由于二叉树的每个结点至多有两个孩子，故"第(i+1)层上的结点数目" 最多是 "第i层的结点数目的2倍"。即，第(i+1)层上的结点数目最大值=2×2^{i-1}=2^{i}。
                故假设成立，原命题得证！

 

2.2 性质2：深度为k的二叉树至多有2^{k}-1个结点(k≥1)

证明：在具有相同深度的二叉树中，当每一层都含有最大结点数时，其树中结点数最多。利用"性质1"可知，深度为k的二叉树的结点数至多为：
           2⁰+2¹+…+2^k-1=2^k-1
           故原命题得证！

 

2.3 性质3：包含n个结点的二叉树的高度至少为log₂ (n+1)

证明：根据"性质2"可知，高度为h的二叉树最多有2^{h}–1个结点。反之，对于包含n个节点的二叉树的高度至少为log₂(n+1)。

 

2.4 性质4：在任意一棵二叉树中，若终端结点的个数为n₀，度为2的结点数为n₂，则n₀=n₂+1

证明：因为二叉树中所有结点的度数均不大于2，所以结点总数(记为n)="0度结点数(n₀)" + "1度结点数(n₁)" + "2度结点数(n₂)"。由此，得到等式一。
         (等式一) n=n₀+n₁+n₂
　     另一方面，0度结点没有孩子，1度结点有一个孩子，2度结点有两个孩子，故二叉树中孩子结点总数是：n₁+2n₂。此外，只有根不是任何结点的孩子。故二叉树中的结点总数又可表示为等式二。
         (等式二) n=n₁+2n₂+1
        由(等式一)和(等式二)计算得到：n₀=n₂+1。原命题得证！

 

3. 满二叉树，完全二叉树和二叉查找树

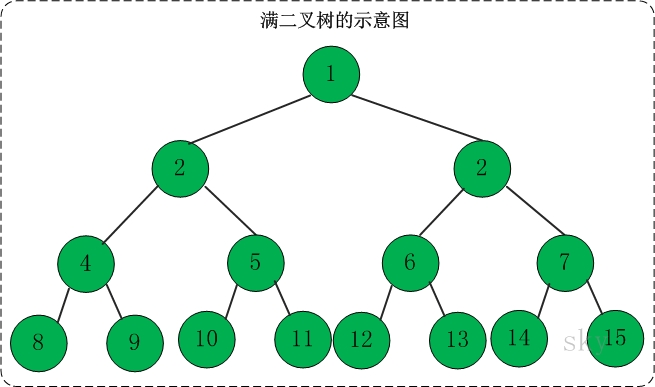
3.1 满二叉树

定义：高度为h，并且由2^{h} –1个结点的二叉树，被称为满二叉树。

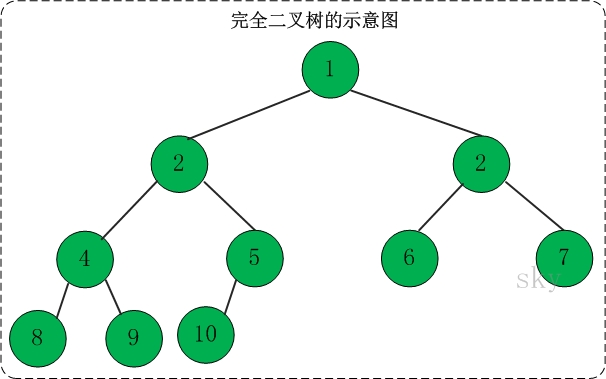
3.2 完全二叉树

定义：一棵二叉树中，只有最下面两层结点的度可以小于2，并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。
特点：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。显然，一棵满二叉树必定是一棵完全二叉树，而完全二叉树未必是满二叉树。

3.3 二叉查找树

定义：二叉查找树(Binary Search Tree)，又被称为二叉搜索树。设x为二叉查找树中的一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。

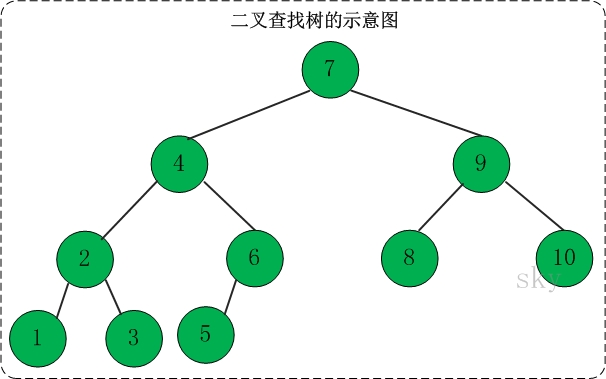
在二叉查找树中：
(01) 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
(02) 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
(03) 任意节点的左、右子树也分别为二叉查找树。
(04) 没有键值相等的节点（no duplicate nodes）。

java实现树bean：

package com.sly.uploadfile.algorithm;

/**
 * Created by fmgao on 2019/7/24.
 */
public class TreeNode01<T> {
    T value;
    TreeNode01<T> leftChild;
    TreeNode01<T> rightChild;

    TreeNode01() {
    }

    TreeNode01(T value) {
        this.value = value;
    }

    /**
     * 增加左子节点
     *
     * @param value
     */
    public void addLeft(T value) {
        TreeNode01<T> leftChild = new TreeNode01<T>();
        this.leftChild = leftChild;

    }

    /**
     * 增加右子节点
     *
     * @param value
     */
    public void addRight(T value) {
        TreeNode01<T> rightChild = new TreeNode01<>();
        this.rightChild = rightChild;
    }

    @Override
    public boolean equals(Object obj) {
        if (!(obj instanceof TreeNode01)) {
            return false;
        }
        return this.value.equals(((TreeNode01<?>) obj).value);
    }

    @Override
    public int hashCode() {
        return this.value.hashCode();
    }

    @Override
    public String toString() {
        return this.value == null ? "" : this.value.toString();
    }
}

 

java基本操作：

package com.sly.uploadfile.algorithm;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

/**
 * Created by fmgao on 2019/7/24.
 */
public class TreeNodeTools {

    /**
     * 判断树种节点个数
     *
     * @param root
     * @param <T>
     * @return
     */
    public static <T> int getTreeNum(TreeNode01<T> root) {
        if (root == null) {
            return 0;
        }
        return getTreeNum(root.leftChild) + getTreeNum(root.rightChild) + 1;
    }

    /**
     * 判断树的深度
     *
     * @param root
     * @param <T>
     * @return
     */
    public static <T> int getTreeDepth(TreeNode01<T> root) {
        if (root == null) {
            return 0;
        }
        int leftDepth = getTreeDepth(root.leftChild) + 1;
        int rightDepth = getTreeDepth(root.rightChild) + 1;
        return Math.max(leftDepth, rightDepth);
    }

    /**
     * 前序遍历
     *
     * @param root
     * @param <T>
     */
    public static <T> void preOrderTravel(TreeNode01<T> root) {
        if (root == null) {
            return;
        }
        visitNode(root);
        preOrderTravel(root.leftChild);
        preOrderTravel(root.rightChild);

    }

    /**
     * 中序遍历
     *
     * @param root
     * @param <T>
     */
    public static <T> void midOrderTravel(TreeNode01<T> root) {
        if (root == null) {
            return;
        }
        midOrderTravel(root.leftChild);
        visitNode(root);
        midOrderTravel(root.rightChild);

    }

    /**
     * 后续遍历
     *
     * @param root
     * @param <T>
     */
    public static <T> void backOrderTravel(TreeNode01<T> root) {
        if (root == null) {
            return;
        }
        backOrderTravel(root.leftChild);
        backOrderTravel(root.rightChild);
        visitNode(root);

    }

    /**
     * 访问node节点
     *
     * @param node01
     * @param <T>
     */
    public static <T> void visitNode(TreeNode01<T> node01) {
        System.out.println(node01.value + "\t");
    }

    /**
     * 分层遍历
     *
     * @param root
     * @param <T>
     */
    public static <T> void levelTravel(TreeNode01<T> root) {
        Queue<TreeNode01<T>> q = new LinkedList<TreeNode01<T>>();
        q.offer(root);
        while (!q.isEmpty()) {
            TreeNode01<T> tmp = q.poll();
            visitNode(tmp);
            if (tmp.leftChild != null) {
                q.offer(tmp.leftChild);
            }
            if (tmp.rightChild != null) {
                q.offer(tmp.rightChild);
            }
        }

    }

    /**
     * 求第K层节点个数
     *
     * @param root
     * @param k
     * @param <T>
     * @return
     */
    public static <T> int getNumForKLevel(TreeNode01<T> root, int k) {
        if (root == null || k < 1) {
            return 0;
        }
        if (k == 1) {
            return 1;
        }
        int leftNum = getNumForKLevel(root.leftChild, k - 1);
        int rightNum = getNumForKLevel(root.rightChild, k - 1);
        return leftNum + rightNum;
    }

    /**
     * 求二叉树种叶子节点的个数
     *
     * @param root
     * @param <T>
     * @return
     */
    public static <T> int getLeafNum(TreeNode01<T> root) {
        if (root == null) {
            return 0;
        }
        if (root.leftChild == null && root.rightChild == null) {
            return 1;
        }
        int leftNum = getLeafNum(root.leftChild);
        int rightNum = getLeafNum(root.rightChild);
        return leftNum + rightNum;
    }

    /**
     * 交换根节点的左右子树
     *
     * @param root
     * @param <T>
     * @return
     */
    public static <T> TreeNode01<T> exchange(TreeNode01<T> root) {
        if (root == null) {
            return null;
        }
        TreeNode01<T> left = exchange(root.leftChild);
        TreeNode01<T> right = exchange(root.rightChild);
        root.leftChild = right;
        root.rightChild = left;
        return root;
    }

    /**
     * 查看node是否是root的节点
     *
     * @param root
     * @param node
     * @param <T>
     * @return
     */
    public static <T> boolean nodeIsChild(TreeNode01<T> root, TreeNode01<T> node) {
        if (root == null || node == null) {
            return false;
        }
        if (root == node) {
            return true;
        }
        boolean isFind = nodeIsChild(root.leftChild, node);
        if (!isFind) {
            isFind = nodeIsChild(root.rightChild, node);
        }
        return isFind;
    }

    /**
     * 返回lNode 和 rNode 以root为根节点的公共父节点
     *
     * @param root
     * @param lNode
     * @param rNode
     * @param <T>
     * @return
     */
    public static <T> TreeNode01<T> findAllFatherNode(TreeNode01<T> root, TreeNode01<T> lNode, TreeNode01<T> rNode) {
        if (lNode == root || rNode == root) {
            return root;
        }
        if (root == null || lNode == null || rNode == null) {
            return null;
        }
        // 如果lNode是左子树的节点
        if (nodeIsChild(root.leftChild, lNode)) {
            if (nodeIsChild(root.rightChild, rNode)) {
                return root;
            } else {
                return findAllFatherNode(root.leftChild, lNode, rNode);
            }
        } else {
            if (nodeIsChild(root.leftChild, rNode)) {
                return root;
            } else {
                return findAllFatherNode(root.rightChild, lNode, rNode);
            }
        }
    }

    /**
     * 根据前序和中序构建二叉树
     *
     * @param pre
     * @param mid
     * @param <T>
     * @return
     */
    public static <T> TreeNode01<T> getTreeFromPreAndMid(List<T> pre, List<T> mid) {
        if (pre == null || mid == null || pre.size() == 0 || mid.size() == 0) {
            return null;
        }
        if (pre.size() == 1) {
            return new TreeNode01<T>(pre.get(0));
        }
        TreeNode01<T> root = new TreeNode01<T>(pre.get(0));
        // 找出根节点在中序中的位置
        int index = 0;
        while (!mid.get(index++).equals(pre.get(0))) {

        }

        // 构建左子树的前序
        List<T> preLeft = new ArrayList<T>(index);

        // 中子树的前序
        List<T> midLeft = new ArrayList<T>(index);
        for (int i = 1; i < index; i++) {
            preLeft.add(pre.get(i));
        }
        for (int i = 0; i < index - 1; i++) {
            midLeft.add(mid.get(i));
        }
        // 重建左子树
        root.leftChild = getTreeFromPreAndMid(preLeft, midLeft);
        // 右子树的前序
        List<T> preRight = new ArrayList<T>(pre.size() - index - 1);
        // 右子树的中序
        List<T> midRight = new ArrayList<T>(pre.size() - index - 1);
        for (int i = 0; i <= pre.size() - index - 1; i++) {
            preRight.add(pre.get(index + i));
        }

        for (int i = 0; i <= pre.size() - index - 1; i++) {
            midRight.add(mid.get(index + i));
        }
        // 重建→子树
        root.rightChild = getTreeFromPreAndMid(preRight, midRight);
        return root;

    }

    public static <T> boolean equals(TreeNode01<T> node1, TreeNode01<T> node2) {
        if (node1 == null && node2 == null) {
            return true;
        } else if (node1 == null || node2 == null) {
            return false;
        }
        boolean isEqual = node1.value.equals(node2.value);
        boolean isLeftEqual = equals(node1.leftChild, node2.leftChild);
        boolean isRightEqual = equals(node1.rightChild, node2.rightChild);
        return isEqual && isLeftEqual && isRightEqual;

    }

}