机器学习之支持向量机
支持向量机模型
支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。
SVM之sklearn实现
线性SVM模型:
from sklearn.svm import LinearSVC LinearSVC(penalty='l2' , c=1.0 , loss='squared_hige' , fit_intercept=True , class_weight=None , max_iter=1000 , tol=0.0001 , multi_class='ovr' , dual=True , intercept_scaling=1)
参数:
pemalty:指定似然函数中加入正则化项,默认为l2,表示添加L2正则项,也可以使用l1,表示添加L1正则项
c:指定正则项的权重,是正则化项惩罚系数的倒数,所以c越小,正则化惩罚项就越大
loss:选择损失函数,可以选择Hinge(合页损失函数)或者squared_hinge(合页损失函数的平方),默认为squared_hinge
fit_intercept:选择是否计算偏置常数b,默认为True ,表示计算
class_weight:指定各类别的权重,默认为None,当样本很不均衡时使用balanced
max_iter:设定最大迭代次数,默认为100次
tol:设定判断迭代收斂函数,默认为0.0001
multi_class:指定多分类的策略,默认为ovr ,表示采用one-vs-rest,一对其他策略。选择multinomial ,表示直接采用多项Logistic回归策略
dual:选择是否采用对偶方式求解,默认为False。只有penalty = ‘l2‘ 且solver = ‘liblinear’时才存在对偶形式
intercept_scaling:该参数默认为1
属性:
coef_:用于输出线性回归模型的权重向量w
intercept_:用于输出线性回归模型的偏置常数b
方法:
fit(X_train ,y_train):进行模型训练
score(X_test ,y_test):返回模型在测试集上的预测准确率
predict(X):用训练好的模型来预测待预测数据集X,返回数据为预测集对应的预测结果yˆ
非线性SVM模型:
from sklearn.svm import SVC SVC(c=1.0 , kernel='rbf' , degree=3 , gamma='auto' , coef0=0.0 , tol=0.0001 , class_weight=None , max_iter=-1)
参数:
c:指定正则项的权重,是正则化项惩罚系数的倒数,所以c越小,正则化惩罚项就越大
kernel:指定核函数类型,选项:linear:线性核函数,poly:多项式核函数,rbf:高斯核函数,Sigmoid:多层感知机核函数,precomputed:表示已经提供一个kernel矩阵
degree:当核函数是多项式函数时,指定p值,默认为3
class_weight:指定各类别的权重,默认为None,当样本很不均衡时使用balanced
gamma:指定多项式核函数或高斯核函数的系数,当选择其他核函数时,忽略该系数,默认为auto
max_iter:设定最大迭代次数,默认为100次
tol:设定判断迭代收斂函数,默认为0.0001
coef0:当核函数是poly或Sigmoid时,指定其r值,默认为0
属性:
coef_:用于输出线性回归模型的权重向量w
intercept_:用于输出线性回归模型的偏置常数b
support_:支持向量的下标
support_vectors_:支持向量
n_support_:每一个分类的支持向量的个数
方法:
fit(X_train ,y_train):进行模型训练
score(X_test ,y_test):返回模型在测试集上的预测准确率
predict(X):用训练好的模型来预测待预测数据集X,返回数据为预测集对应的预测结果yˆ
predict_proba(X):返回一个数组,数组元素依次为预测集X属于各个类别的概率
predict_log_proba(X):返回一个数组,数组的元素依次是预测集X属于各个类别的对数概率
svm模型案例
from sklearn.datasets import make_circles from sklearn.preprocessing import StandardScaler import matplotlib.pyplot as plt from matplotlib.colors import ListedColormap import numpy as np from sklearn.svm import SVC X ,y = make_circles(noise=0.2 ,factor=0.5 ,random_state=1) X = StandardScaler().fit_transform(X) x_min ,x_max = X[: ,0].min() - 1 ,X[: ,0].max() + 1 y_min ,y_max = X[: ,1].min() - 1 ,X[: ,1].max() + 1 xx ,yy = np.meshgrid(np.arange(x_min ,x_max ,0.02),np.arange(y_min ,y_max ,0.02)) C = 5 gamma = 0.1 clf = SVC(C=C ,gamma = gamma) clf.fit(X ,y) z = clf.predict(np.c_[xx.ravel() ,yy.ravel()])
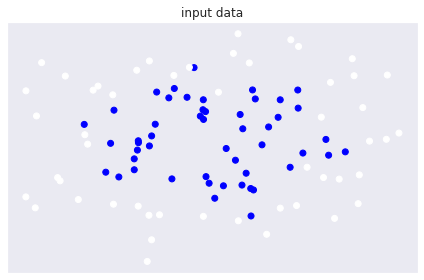
原始数据图例:
cm = plt.cm.RdBu cm_bright = ListedColormap(['#FFFFFF' ,'#0000FF']) ax = plt.subplot() ax.set_title('input data') ax.scatter(X[: ,0] ,X[: ,1] ,c = y ,cmap = cm_bright) ax.set_xticks(()) ax.set_yticks(()) plt.tight_layout() plt.show()
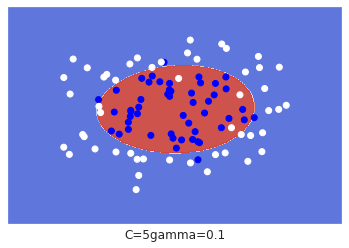
模型图例:
z = z.reshape(xx.shape) plt.subplot() plt.contourf(xx ,yy ,z ,cmap = plt.cm.coolwarm ,alpha = 0.9) plt.scatter(X[: ,0] ,X[: ,1] ,c = y ,cmap= cm_bright) plt.xlim(xx.min() ,xx.max()) plt.ylim(yy.min() ,yy.max()) plt.xticks(()) plt.yticks(()) plt.xlabel("C=" + str(C) + "gamma=" + str(gamma)) plt.show()
SVM之小结
1、优点:
1、SVM具有较好的泛化能力,特别是在小样本训练集上能够得到比其他算法好很多的结果,因为其优化目标是结构风险最小,而不是经验风险最小,通过margin的概念,可以得到对数据分布的结构化描述,从而降低对数据规模和数据分布的要求。
2、SVM具有较强的数学理论支撑,基本不涉及概率预测度和大数定律等。
3、引入核函数后可以解决非线性分类问题。
2、缺点:
1、不方便解决多分类问题,经典的SVM模型只给出了二分类算法。
2、SVM模型存在两个对结果影响超大的参数,比如采用rbf核函数时,超函数惩罚项系数c和核函数参数gamma是无法通过概率的方法进行计算的,只能通过穷举遍历的方式或者根据以往经验推测获得,导致其复杂度比一般的线性分类器要高。
3、SVM与logistic异同点:
1、SVM模型和LR模型都是监督模型算法,都属于判别模型。
2、如果不考虑核函数,二者都是线性分类问题。
3、构造原理不同:LR模型使用Sigmoid函数来映射出属于某一类别的概率,然后构造log损失,通过极大似然估计来求解模型参数的值;SVM模型使用函数间隔最大化来寻找最优超平面,对应的是Hinge损失。
4、SVM与LR学习时考虑的样本不同:LR模型学习过程中会使用全量的训练集样本数据;而SVM模型学习过程中只使用支持向量点,即只考虑离分割超平面在一定范围的样本点。
5、SVM模型通过引入核函数的方法,可以解决非线性问题,而LR模型一般没有核函数的概念。
6、SVM模型中自带正则化项,与LR模型相比,更不容易发生过拟合。


