机器学习之K近邻

KNN模型定义：

　　K近邻（K-Nearest Neighber，俗称KNN模型）。

　　其思想是：对于任意一个新的样本点，我们可以在M个已知类别标签的样本点中选取K个与其距离最接近的点作为她的最近邻近点，然后统计这K个最近邻近点的类别标签，采取多数投票表决的方式，把K个最近邻点中占绝大多数类别的点所对应的类别拿来当作要预测点的类别。

　　K近邻模型三要素：K值的选择、距离度量方法、分类决策规则。

K值的选择：K值的选择决定了特征空间被划分成的子空间数量，K值较大时，相当于对空间特征进行较复杂的划分，因而对应的模型自然会变得更加复杂，容易发生过拟合，反之容易发生欠拟合。在实际工业中，一般采用交叉验证来选取合适的K值。

距离度量：距离度量包括曼哈顿距离、欧氏距离、闵可夫斯基距离等，一般使用较多的是欧氏距离。在使用距离度量之前，一般需要对数据进行归一化处理，如果不做归一化处理，取值较小但实际比较重要的特征参数的作用有可能会被淹掉。

分类决策规则：K近邻主要使用多数表决规则。目标是使得误分类概率L最小化，K近邻的多数表决规则等价于使训练数据的经验风险最小化

　　搜索优化：1、购造KD树 ，构造KD树的过程相当于不断地用垂直于坐标轴的超平面对K维空间进行切分，构造成一系列的K维超矩形区域，KD树的每个节点对应一个K维超矩形区域。2、搜索KD树，先从根节点出发，递归向下访问KD树，若目标当前维的坐标小鱼切分点坐标，则移动到左子节点，否则移动到右子节点，直到子节点为叶子节点为止。

 

KNN的sklearn实现

knn模型（分类与回归参数方法一致）：

from sklearn.neighbors import KNeighborsClassifier
from sklearn.neighbors import KNeighborsRegressor
KNeighborsClassifier(n_neighbors=5 ,
                     weights='uniform' ,
                     algorithm='auto' ,
                     leaf_size=30 ,
                     metric='minkowski' ,
                     p=2 ,
                     n_jobs=-1)

参数：

　　n_neighbors：指定最近邻点个数，默认为5 

　　wieghts：指定投票权重类型，默认为uniform，表示K个最近邻点的投票权重均等，distance表示K个最近邻点最后的投票权重与它们距离待预测点的距离成反比

　　algorithm：指定寻找最近邻点的算法，默认为auto表示自动选择。可以指定为kd_tree（KD树算法）、ball_tree（BallTree算法）、brute（暴力搜索法）

　　leaf_size：指定KD树算法或者BallTree算法中叶子节点的数目，默认为30

　　metric：指定距离度量的类型，默认为minkowski（闵可夫斯基距离），和后面的参数p配合使用

　　p：配合metric使用，当p=1时为曼哈顿距离，当p=2时为欧氏距离，默认为欧氏距离

　　n_job：略....

方法：

　　fit(X_train ,y_train)：进行模型训练

　　score(X_test ,y_test)：返回模型在测试集上的预测准确率

　　predict(X)：用训练好的模型来预测待预测数据集X，返回数据为预测集对应的预测结果y^ˆ

　　predict_proba(X)：返回一个数组，数组元素依次为预测集X属于各个类别的概率

　　kneighbors([X ,n_neighbors ,return_distance])：返回待预测样本点的K个最近邻点，当return_distance=True时，返回这些最近邻点对应的距离

　　kneighbors_graph([X ,n_neighbors ,model])：返回样本的连接图

 

KNN案例之鸢尾花：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.neighbors import KNeighborsClassifier
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data[:,:2]
y = iris.target

cmap_light = ListedColormap(['#FFAAAA' ,'#AAFFAA' ,'#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000' ,'#00FF00' ,'#0000FF'])

#n_neighbors = 15 ,weights = 'uniform'
n_neighbors = 15
weights = 'uniform'
clf = KNeighborsClassifier(n_neighbors= 15 ,weights= 'uniform')
clf.fit(X,y)

x_min ,x_max = X[:,0].min() - 1 ,X[:,0].max() + 1
y_min ,y_max = X[:,1].min() - 1 ,X[:,1].max() + 1

xx ,yy = np.meshgrid(np.arange(x_min ,x_max , 0.02) ,np.arange(y_min ,y_max , 0.02))
z = clf.predict(np.c_[xx.ravel() ,yy.ravel()])
z = z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx ,yy ,z ,cmap = cmap_light)

plt.scatter(X[:,0] ,X[:,1] ,c= y ,cmap = cmap_bold)
plt.xlim(xx.min() ,xx.max())
plt.ylim(yy.min() ,yy.max())
plt.title("3-Class classification(k = %i ,weights = '%s')"%(n_neighbors ,weights))
plt.show()

#n_neighbors = 15 ,weights = 'distance'
n_neighbors = 15
weights = 'distance'
clf2 = KNeighborsClassifier(n_neighbors= 15 ,weights= 'distance')
clf2.fit(X,y)

x_min ,x_max = X[:,0].min() - 1 ,X[:,0].max() + 1
y_min ,y_max = X[:,1].min() - 1 ,X[:,1].max() + 1

xx ,yy = np.meshgrid(np.arange(x_min ,x_max , 0.02) ,np.arange(y_min ,y_max , 0.02))
z = clf2.predict(np.c_[xx.ravel() ,yy.ravel()])
z = z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx ,yy ,z ,cmap = cmap_light)

plt.scatter(X[:,0] ,X[:,1] ,c= y ,cmap = cmap_bold)
plt.xlim(xx.min() ,xx.max())
plt.ylim(yy.min() ,yy.max())
plt.title("3-Class classification(k = %i ,weights = '%s')"%(n_neighbors ,weights))
plt.show()

 

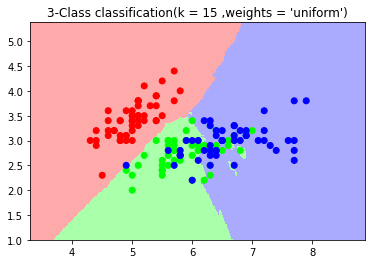
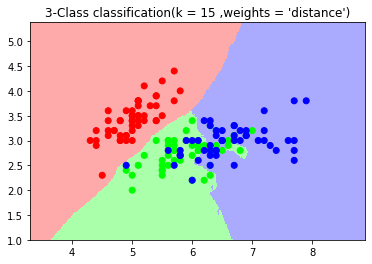
 KNN之小结

1、优点：简单易实现，比较适合多分类问题，对异常值不太敏感，无数据输入假定

2、缺点：预测精度一般，对于大部分问题比不上基于树的方法；当样本存在范围重叠时，分类精度很低；分类一个样本需要计算所有数据，不太适应大数据环境

3、场景：比较适合小量且精度要求不高的数据 ，比较适合不能一次性获取训练样本的情况

4、注意点：三个对结果影响较大的参数：数据归一化，K值的选择，距离的度量方式，距离的计算方式是K近邻的核心，一般使用较多的是欧氏距离