模型之各个指标

Woe公式如下：

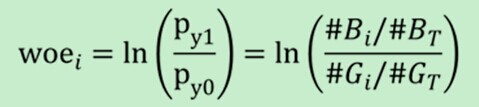
woe反映的是在自变量每个分组下违约用户对正常用户占比和总体中违约用户对正常用户占比之间的差异。

IV公式如下：

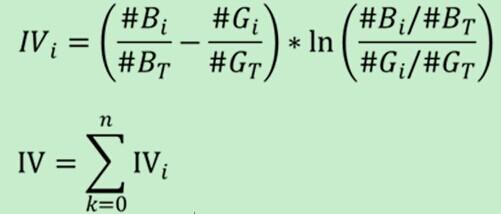
IV衡量的是某一个变量的信息量，相当于是自变量woe值的一个加权求和，其值的大小决定了自变量对于目标变量的影响程度；从另一个角度来看的话，IV公式与信息熵的公式极其相似。

Gini的计算公式：

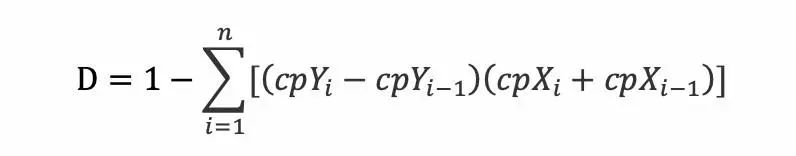
Gini指数最早应用在经济学中，主要用来衡量收入分配公平度的指标。在决策树算CART算法中用gini指数来衡量数据的不纯度或者不确定性，同时用gini指数来决定类别变量的最优二分值得切分问题。运用在评分模型中它也是表征评分模型的区分能力。

其中 cpx 为劳伦斯曲线的横轴，cpy 为纵轴，i 为第 i 个坐标，cpxi 为第 i 个坐标的横坐标，表示累积样本量比例，cpyi 为第 i 个坐标的纵坐标，表示累积样本数值比例；

gini区间：

（

针对评分卡集来说，申请评分卡集的通识标准：

1) Gini<0.3,模型不太能接受；

2) 0.3<=Gini<0.35,模型区分能力一般，模型有优化空间；

3) 0.35<=Gini<=0.5,模型区分能力比较满意；

4) Gini>0.5，Gini越高越有过拟的可能性；

行为评分卡集的通史标准：

1) Gini可能会超过0.8；

2) Gini<0.6，可能模型有问题。

）

参考文档：https://www.zhihu.com/question/20219466/answer/766668286

KS公式：

KS(Kolmogorov-Smirnov)值越大，表示模型能够将正、负客户区分开的程度越大。KS值的取值范围是[0，1] ，ks越大，表示计算预测值的模型区分好坏用户的能力越强。

KS（Kolmogorov-Smirnov）检验:K－S检验主要是验证模型对违约对象的区分能力，通常是在模型预测全体样本的信用评分后，将全体样本按违约与非违约分为两部分，然后用KS统计量来检验这两组样本信用评分的分布是否有显著差异。

分箱内，max（累计坏的/坏的总数 - 累计好的/好的总数）

参考文档：https://blog.csdn.net/sscc_learning/article/details/86707005

AUC公式：

公式的含义见：公式解释

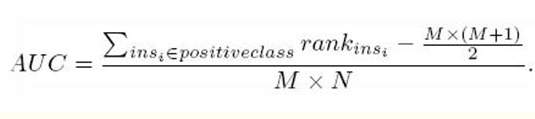
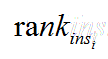，代表第i条样本的序号。（概率得分从小到大排，排在第rank个位置）

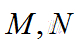分别是正样本的个数和负样本的个数

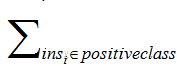只把正样本的序号加起来。

AUC（are under curve)是一个模型的评价指标，用于分类任务。这个指标想表达的含义，简单来说其实就是随机抽出一对样本（一个正样本，一个负样本），然后用训练得到的分类器来对这两个样本进行预测，预测得到正样本的概率大于负样本概率的概率。

参考文档：https://blog.csdn.net/qq_22238533/article/details/78666436

roc曲线：

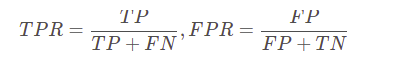
ROC曲线及AUC系数主要用来检验模型对客户进行正确排序的能力。ROC曲线描述了在一定累计好客户比例下的累计坏客户的比例，模型的分别能力越强，ROC曲线越往左上角靠近。AUC系数表示ROC曲线下方的面积。AUC系数越高，模型的风险区分能力越强。

1、ROC曲线之间没有交点：

如下图所示，A，B，C三个模型对应的ROC曲线之间交点，且AUC值是不相等的，此时明显更靠近

2、ROC曲线之间存在交点：

如下图所示，模型A、B对应的ROC曲线相交却AUC值相等，此时就需要具体问题具体分析：当需要高Sensitivity值时，A模型好过B；当需要高Specificity值时，B模型好过A。

在这里插入图片描述

F1-Score:

一、什么是F1-score

F1分数（F1-score）是分类问题的一个衡量指标。一些多分类问题的机器学习竞赛，常常将F1-score作为最终测评的方法。它是精确率和召回率的调和平均数，最大为1，最小为0。

$F_{1}=2\cdot \frac{precision\cdot recall}{precision+recall}$

此外还有F2分数和F0.5分数。F1分数认为召回率和精确率同等重要，F2分数认为召回率的重要程度是精确率的2倍，而F0.5分数认为召回率的重要程度是精确率的一半。计算公式为：

$F_{\beta }=\left (1+\beta ^{2} \right )\cdot \frac{precision\cdot recall}{\left (\beta ^{2}\cdot precision \right )+recall}$

G分数是另一种统一精确率和的召回率系统性能评估标准，G分数被定义为召回率和精确率的几何平均数。

$G=\sqrt{precision\cdot recall}$

二、计算过程

1. 首先定义以下几个概念：

TP（True Positive）：预测答案正确

FP（False Positive）：错将其他类预测为本类

FN（False Negative）：本类标签预测为其他类标

2. 通过第一步的统计值计算每个类别下的precision和recall

精准度 / 查准率(precision)：指被分类器判定正例中的正样本的比重

$precision_{k}=\frac{TP}{TP+FP}$

召回率 / 查全率 (recall)：指的是被预测为正例的占总的正例的比重

$recall_{k}=\frac{TP}{TP+FN}$

另外，介绍一下常用的准确率(accuracy)的概念，代表分类器对整个样本判断正确的比重。

$accuracy=\frac{TP+TN}{TP+TN+FP+FN}$

3. 通过第二步计算结果计算每个类别下的f1-score，计算方式如下：

$f1_{k}=\frac{2\cdot precision_{k}\cdot recall_{k} }{precision_{k}+recall_{k}}$

4. 通过对第三步求得的各个类别下的F1-score求均值，得到最后的评测结果，计算方式如下：

$score=(\frac{1}{n}\sum f1_{k})^{2}$

示例程序:

from sklearn.metrics import f1_score
 
y_pred = [0, 1, 1, 1, 2, 2]
y_true = [0, 1, 0, 2, 1, 1]
 
print(f1_score(y_true, y_pred, average='macro'))  
print(f1_score(y_true, y_pred, average='weighted'))

分析上述代码，

对于类0：TP=1，FP=0，FN=1，precision=1，recall=1/2，F1-score=2/3，Weights=1/3

对于类1：TP=1，FP=2，FN=2，precision=1/3，recall=1/3，F1-score=1/3，Weights=1/2

对于类2：TP=0，FP=2，FN=1，precision=0，recall=0，F1-score=0，Weights=1/6

宏平均分数为：0.333；加权平均分数为：0.389

参考文档：https://blog.csdn.net/qq_14997473/article/details/82684300

PSI公式：

群体稳定性指标PSI(Population Stability Index)是衡量模型的预测值与实际值偏差大小的指标。

训练一个logistic回归模型，预测时候会有个概率输出p。测试集上的输出设定为p1吧，将它从小到大排序后10等分，如0-0.1,0.1-0.2,......。现在用这个模型去对新的样本进行预测，预测结果叫p2，按p1的区间也划分为10等分。实际占比就是p2上在各区间的用户占比，预期占比就是p1上各区间的用户占比。

意义就是如果模型跟稳定，那么p1和p2上各区间的用户应该是相近的，占比不会变动很大，也就是预测出来的概率不会差距很大。一般认为PSI小于0.1时候模型稳定性很高，0.1-0.25一般，大于0.25模型稳定性差，建议重做。

odds公式：

极大似然估计：

多重共线性：

正则化：

损失函数：

最大似然法：

卡方检验：

posted @ 2020-12-02 15:27 17孤独的牧羊人阅读(710) 评论(0) 编辑收藏举报

刷新页面返回顶部

17孤独的牧羊人