上取整与下取整的转换
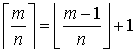
这上面的结果也是鸽巢原理的结果,将m个球放入n个盒子,则存在一个盒子里面至少有ceil(m/n)=floor((m-1)/n)+1 个球,同时还存在一个盒子里面至多有floor(m/n)个球。
广义鸽巢原理(退化的Ramsey定理)
第一个盒子有不少于R1个球,
或者第二个盒子有不少于R2个球,
...
或者第n个盒子有不少于Rn个球。
则总球数不少于(R1 + R2 + ... + Rn - n + 1)个球。
注意上面的条件之间为或者关系,不是所有的盒子i都满足不少于Ri个球。
取R1=R2=...=Rn=p。则有总球数不少于n*p-n+1个。即当有m=n*p-n+1个球的时候,放入n个盒子,能保证存在一个盒子里面至少有球不少于p个。
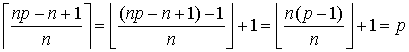



 浙公网安备 33010602011771号
浙公网安备 33010602011771号