二叉树的四种遍历方法笔记
- 二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中所有的结点,使得每个结点被访问依次且仅被访问一次。
| 前序 | 中 | 左 | 右 |
|---|---|---|---|
| 中序 | 左 | 中 | 右 |
| 后序 | 左 | 右 | 中 |
st=>start: 开始
e=>end: 结束
op=>operation: 根结点
op2=>operation: 左子树
io=>inputoutput: 右子树
cond=>condition: 二叉树是否为空?
st->cond
cond(yes)->e
cond(no)->e
op->op2->io->e
- 前序遍历
若树为空,则空操作返回。否则,先访问根节点,然后前序遍历左子树,再前序遍历右子树。(W)型 (中 左 右)
 

- 中序遍历
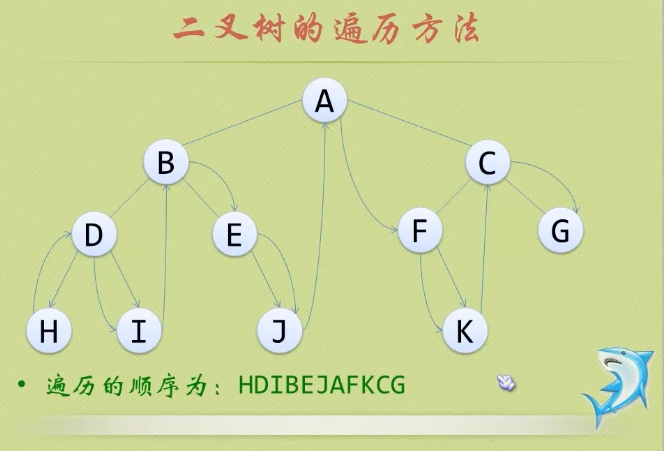
若树为空,则空操作返回。否则,从根节点开始(注意并不是先访问根节点),中序遍历根节点的左子树,然后是访问根节点,最后中序遍历根节点的右子树。(M)型,(左 中 右)

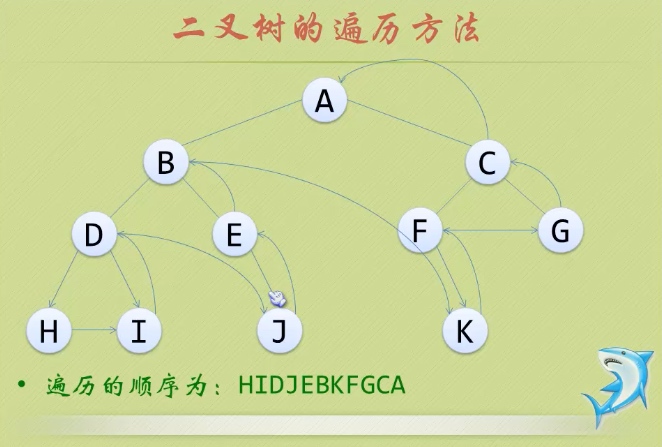
- 后续遍历
若树为空,则空操作返回。否则,从左到右先叶子后节点的方式遍历访问左右子树,最后访问根节点。(左右中)逆时针型 (左 右 中)

- 层序遍历
若树为空,则空操作返回。否则,从树的第一层,也就是根节点开始访问,从上到下逐层遍历,在同一层中,按从左到右的顺序结点逐个访问。
 




