CS231N assignment2 SVM
CS231N Assignment2 Support Vector Machine
Begin
本文主要介绍CS231N系列课程的第一项作业,写一个SVM无监督学习训练模型。
课程主页:网易云课堂CS231N系列课程
语言:Python3.6
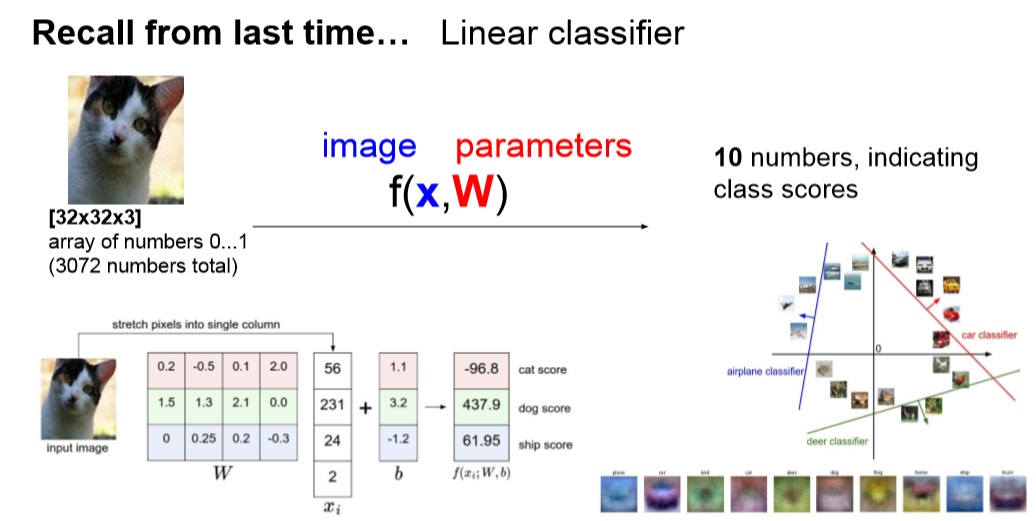
1线形分类器
以图像为例,一幅图像像素为32*32*3代表长32宽32有3通道的衣服图像,将其变为1*3072的一个向量,即该图像的特征向量。
我们如果需要训练1000幅图像,那么输入则为1000*3072的矩阵X。
我们用X点乘矩阵W得到一个计分矩阵如下所示,W乘以一幅图像的特征向量的转置得到一列代表分数。
每个分数对应代表一个类别,分数越高代表她所属于此类别纪律越大,所以W其实是一个类别权重的概念。
注意:下图为CS231N中的一张图,它是以一幅图为例,将X转至为3072*1,大家理解即可,在程序中我们采用X*W来编写。
更多细节可以参考CS231N作业1KNN详解
2损失函数
得到每一幅图像对应每一个类别的分数之后,我们需要计算一个损失,去评估一下W矩阵的好坏。
如下右侧为SVM损失函数计算公式。
对每一幅图像的损失用其错误类别的分数减去正确类别的分数,并与0比较求最大值
一般我们应该正确类别的分数高就证明没有损失,此时错误类别减去正确类别一定为负值,比0小故取损失为0.
为了提高鲁棒性,这里给他加了一个1。

计算所有的损失后,我们把损失累加作为最后的损失
整理后我们得到如下的公式,但是其存在一个问题,没有考虑W的影响,不同的W可能得到同样的损失,
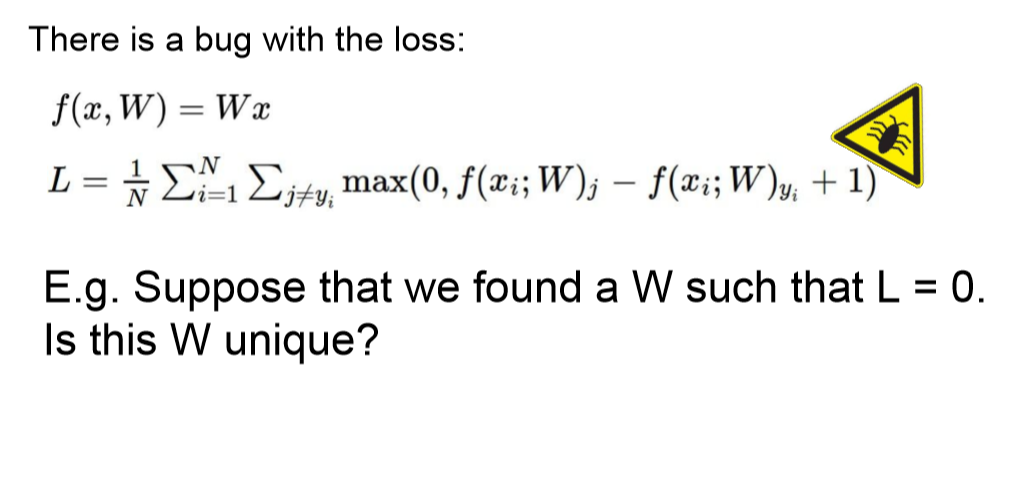
因此我们引入一个正则,正则系数可以调节W对整个损失的影响,W越分散当然越好

代码如下:
def svm_loss_native(W,X,Y,reg):
'''
本函数用于计算SVM分类器的损失以及梯度
输入参数:
W(D,C)代表权重
D为特征向量的维度,C为分类类别的数量
X(N,D)代表训练样本的特征,0维代表每一个样本,1维代表某一样本的特征向量
对于32*32图像,N代表有N个样本,D=32*32*3全体像素值代表特征向量
Y(N,1)代表训练样本的标签,0维代表每一个样本,1维代表某一样本的标签
输出参数:
Loss损失
'''
#获取基础参数
num_train = X.shape[0]#训练样本的数量
num_classes = W.shape[1]#划分的种类
loss = 0.0#初始化损失
dW = np.zeros(W.shape)#创建一个梯度
for i in range(num_train):#分别求每一个训练样本的损失
score = X[i].dot(W)#计算每个样本的分数
#计算损失
for j in range(num_classes):
if j == Y[i]:
continue
margin = score[j] - score[Y[i]] + 1
#margin = np.max(0,score[j] - score[Y[i]] + 1)#计算损失
if margin > 0:
loss += margin
loss /= num_train
#加入正则
loss += reg * np.sum(W*W)
return loss
如此一套完整的损失函数就构造完成了,我们通过看损失可以知道这个W矩阵的好坏,那么如果损失过大该怎么调剂每一个参数呢?
此时我们引入梯度下降法和梯度的概念
3梯度
梯度下降法:
所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向,也就是场景中测量方向的手段。

梯度如同求导一样,如下图所示,损失的导数反应着梯度状况
如果W向前变化一格,损失增大,则dW梯度应该为正值,此时应该W向相反方向变化。

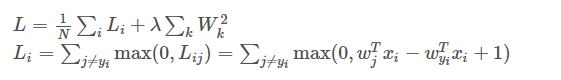
对于Lij,用其对Wj求偏导

CODE2 LOSS & 梯度 循环形式
def svm_loss_native(W,X,Y,reg):
'''
本函数用于计算SVM分类器的损失以及梯度
输入参数:
W(D,C)代表权重
D为特征向量的维度,C为分类类别的数量
X(N,D)代表训练样本的特征,0维代表每一个样本,1维代表某一样本的特征向量
对于32*32图像,N代表有N个样本,D=32*32*3全体像素值代表特征向量
Y(N,1)代表训练样本的标签,0维代表每一个样本,1维代表某一样本的标签
输出参数:
Loss损失
'''
#获取基础参数
num_train = X.shape[0]#训练样本的数量
num_classes = W.shape[1]#划分的种类
loss = 0.0#初始化损失
dW = np.zeros(W.shape)#创建一个梯度
for i in range(num_train):#分别求每一个训练样本的损失
score = X[i].dot(W)#计算每个样本的分数
#计算损失
for j in range(num_classes):
if j == Y[i]:
continue
margin = score[j] - score[Y[i]] + 1
#margin = np.max(0,score[j] - score[Y[i]] + 1)#计算损失
if margin > 0:
loss += margin
dW[:,Y[i]] += -X[i,:].T
dW[:,j] += X[i,:].T
loss /= num_train
dW /= num_train
#加入正则
loss += reg * np.sum(W*W)
dW += reg * W
return loss,dW
CODE3 LOSS & 梯度 向量矩阵形式
def svm_loss_vectorized(W,X,Y,reg):
loss = 0.0
num_train = X.shape[0]
dW = np.zeros(W.shape)
scores = np.dot(X,W)
correct_class_score = scores[np.arange(num_train),Y]
correct_class_score = np.reshape(correct_class_score,(num_train,-1))
margin = scores - correct_class_score + 1.0
margin[np.arange(num_train),Y] = 0.0
margin[margin<0] = 0.0
loss += np.sum(margin)/num_train
loss += 0.5*reg*np.sum(W*W)
margin[margin>0] = 1.0
row_sum = np.sum(margin,axis = 1)
margin[np.arange(num_train),Y] = -row_sum
dW = 1.0/num_train*np.dot(X.T,margin) + reg*W # ** #
return loss,dW
4训练函数
在得到损失和梯度后我们就可以根据梯度去调节W矩阵,这里需要引入TRAIN函数的一些参数。
一般需要有以下参数:
训练次数:要循环训练多少步。
学习率:每一次根据梯度去修正W矩阵的系数。
样本数:每一次训练可能不是选择所有样本,需要取样一定样本。
核心点在于在循环中不断去计算损失以及梯度,然后利用下面公式去调节。
CODE4 梯度下降法
def train(self,X,Y,learning_rate=1e-3,reg=1e-5,num_iters=100,batch_size=200,verbose=False):
'''
随机梯度下降法训练分类器
输入参数:
-learning_rate学习率
-reg正则化强度
-num_iters步长值
-batch_size每一步使用的样本数量
-verbose若为真则打印过程
输出参数:
list损失值
'''
num_train,dim = X.shape
num_classes = np.max(Y) + 1
#if self.W is None:
#初始化W矩阵
self.W = 0.001 * np.random.randn(dim,num_classes)
loss_history = []
#开始训练num_iters步
for it in range(num_iters):
X_batch = None
Y_batch = None
########################
# 选取部分训练样本
# 随机生成一个序列
batch_inx = np.random.choice(num_train,batch_size)
X_batch = X[batch_inx,:]
Y_batch = Y[batch_inx]
#########################
# 计算损失与梯度
loss,grade = self.loss(self.W,X_batch,Y_batch,reg)
loss_history.append(loss)
########################
# 参数更新
# 梯度为正表示损失增大,应该减少,成负相关
self.W = self.W - learning_rate * grade
#打印结果
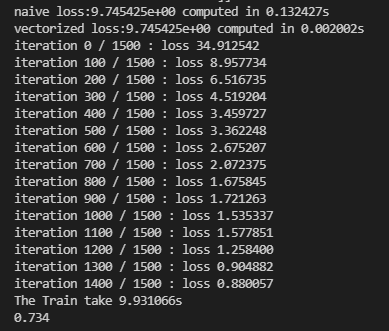
if verbose and it % 100 == 0:
print('iteration %d / %d : loss %f'%(it ,num_iters,loss))
return loss_history
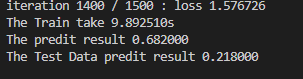
运行结果如
5预测predict
在训练完模型后会得到一个较好的W矩阵,然后根据这个W去预测一下测试集看看模型的效果
def predict(self,X_train):
y_predict = np.zeros(X_train.shape[1])
#根据训练后的W矩阵计算分数
scores = X_train.dot(self.W)
#找到得分中最大的值作为类别
y_predict = np.argmax(scores,axis = 1)#计算每一行最大值
return y_predict
在主函数中运行如下代码观察预测情况
score1 = SVM1.predict(X_dev)
print('The predit result %f' %(np.mean(score1 == Y_dev)))
score1 = SVM1.predict(X_test)
print('The Test Data predit result %f' %(np.mean(score1 == Y_test)))
预测结果如下,用训练集本身去预测得到0.756,用测试集去预测才0.218,不是太好
6参数调整
上述即完成了一整体的SVM模型库,那么我们如何自动训练出一个好的学习率和正则化强度参数呢?
我们需要不断去测试每一个参数的好坏,用下面一个程序可以完成这个任务
#调参
#两个参数,学习率;正则化强度
learning_rate = [2e-7,0.75e-7,1.5e-7,1.25e-7,0.75e-7]
regularization_strengths = [3e4,3.25e4,3.5e4,3.75e4,4e4]
results = {}
best_val = 0
best_svm = None
######################################
# 循环执行代码
# 对不同的学习率以及正则化强度进行测试
#
for rate in learning_rate:
for regular in regularization_strengths:
SVM2 = SVM()
#训练
SVM2.train(X_train,Y_train,learning_rate=rate,reg=regular,num_iters=1000)
#预测
Y1 = SVM2.predict(X_train)
Y2 = SVM2.predict(X_val)
accuracy_train = np.mean(Y1==Y_train)
accuracy_val = np.mean(Y2==Y_val)
#判断优略
if best_val < accuracy_val:
best_val = accuracy_val
best_svm = SVM2#保存当前模型
#存储数据
results[rate,regular] = (accuracy_train,accuracy_val)
#打印数据
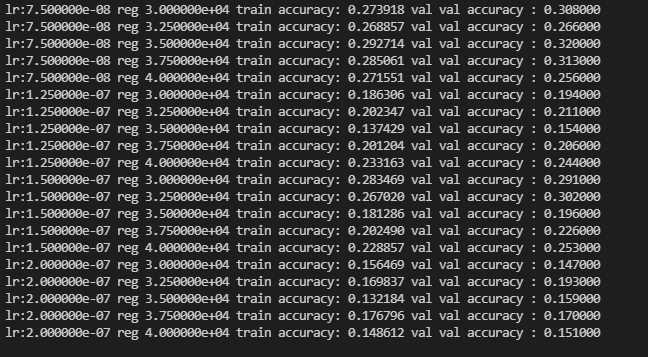
for lr,reg in sorted(results):
accuracy_train,accuracy_val = results[(lr,reg)]
print('lr:%e reg %e train accuracy: %f val val accuracy : %f'%(lr,reg,accuracy_train,accuracy_val))
运行结果如下:
7 可视化效果
在得到最优W时,我们有时要看一下W的可视化效果,从w的图像可以看出权重高低,类似于一个反应这个类别的模板。
#可视化结果数据
w = best_svm.W[:,:]
w=w.reshape(32,32,3,10)
w_min,w_max = np.min(w),np.max(w)
classes = ['plane','car','bird','cat','deer','dog','frog','hors','ships','truck']#类别划分 列表
for i in range(10):
plt.subplot(2,5,i+1)
wimg = 255.0 * (w[:,:,:,i].squeeze()-w_min) / (w_max - w_min)
plt.imshow(wimg.astype('uint8'))
plt.axis('off')
plt.title(classes[i])
plt.show()
如下图所示

不知我这图为啥和别人不一样~~~~~~~看着不够清晰呢?还望大神指点
在完成本案例过程中参考了一些文章和帖子,由于书写过程中没有过多记录,故没有标注出来,如有侵权请联系备注!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号