Matlab K-means聚类

K-means算法是硬聚类算法，是典型的基于原型的目标函数聚类方法的代表，它是数据点到原型的某种距离作为优化的目标函数，利用函数求极值的方法得到迭代运算的调整规则。K-means算法以欧式距离作为相似度测度，它是求对应某一初始聚类中心向量V最优分类，使得评价指标J最小。算法采用误差平方和准则函数作为聚类准则函数.K-means聚类算法采用的是将N*P的矩阵X划分为K个类，使得类内对象之间的距离最大,而类之间的距离最小。

Idx=Kmeans(X,K)
[Idx,C]=Kmeans(X,K) 
[Idx,C,sumD]=Kmeans(X,K) 
[Idx,C,sumD,D]=Kmeans(X,K) 
[…]=Kmeans(…,’Param1’,Val1,’Param2’,Val2,…)

各输入输出参数介绍

X :N*P的数据矩阵
K: 表示将X划分为几类，为整数
Idx :N*1的向量，存储的是每个点的聚类标号
C: K*P的矩阵，存储的是K个聚类质心位置
sumD 1*K的和向量，存储的是类间所有点与该类质心点距离之和
D N*K的矩阵，存储的是每个点与所有质心的距离

[…]=Kmeans(…,'Param1',Val1,'Param2',Val2,…)这其中的参数Param1、Param2等，主要可以设置为如下：
1. ‘Distance’(距离测度)
   'sqEuclidean’ 欧式距离（默认时，采用此距离方式）
   ‘cityblock’ 绝度误差和，又称：L1
   ‘cosine’ 针对向量
   ‘correlation’  针对有时序关系的值
   ‘Hamming’ 只针对二进制数据
2. ‘Start’（初始质心位置选择方法）
   ‘sample’ 从X中随机选取K个质心点
   ‘uniform’ 根据X的分布范围均匀的随机生成K个质心
   ‘cluster’ 初始聚类阶段随机选择10%的X的子样本（此方法初始使用’sample’方法）
    matrix 提供一K*P的矩阵，作为初始质心位置集合
3. ‘Replicates’（聚类重复次数）  整数
         

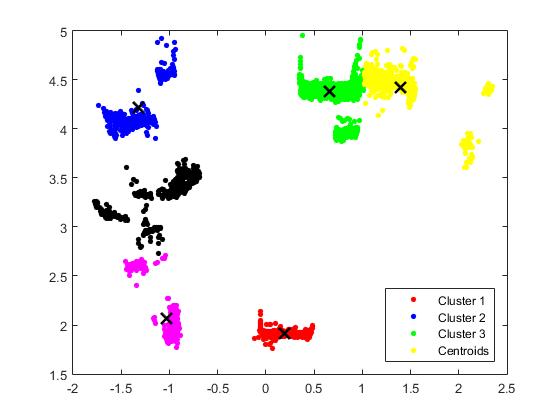
Matlab Kmeans使用案例

X = csvread('4.csv');
[Idx,Ctrs,SumD,D] = kmeans(X,6,'Replicates',3);

%不同颜色表示不同类元素
plot(X(Idx==1,1),X(Idx==1,2),'r.','MarkerSize',14)
hold on
plot(X(Idx==2,1),X(Idx==2,2),'b.','MarkerSize',14)
hold on
plot(X(Idx==3,1),X(Idx==3,2),'g.','MarkerSize',14)
hold on
plot(X(Idx==4,1),X(Idx==4,2),'y.','MarkerSize',14)
hold on
plot(X(Idx==5,1),X(Idx==5,2),'k.','MarkerSize',14)
hold on
plot(X(Idx==6,1),X(Idx==6,2),'m.','MarkerSize',14)

%绘出聚类中心点,kx表示是圆形
plot(Ctrs(:,1),Ctrs(:,2),'kx','MarkerSize',10,'LineWidth',2);
legend('Cluster 1','Cluster 2','Cluster 3','Centroids','Location','SE')

输出结果