卡尔曼滤波

问题的引入

假设你有两个传感器，测的是同一个信号。可是它们每次的读数都不太一样，怎么办？

取平均。

再假设你知道其中贵的那个传感器应该准一些，便宜的那个应该差一些。那有比取平均更好的办法吗？

加权平均。

怎么加权？假设两个传感器的误差都符合正态分布，假设你知道这两个正态分布的方差，用这两个方差值，（此处省略若干数学公式），你可以得到一个“最优”的权重。

接下来，重点来了：假设你只有一个传感器，但是你还有一个数学模型。模型可以帮你算出一个值，但也不是那么准。怎么办？

把模型算出来的值，和传感器测出的值，（就像两个传感器那样），取加权平均。

OK，最后一点说明：你的模型其实只是一个步长的，也就是说，知道x(k)，我可以求x(k+1)。问题是x(k)是多少呢？答案：x(k)就是你上一步卡尔曼滤波得到的、所谓加权平均之后的那个、对x在k时刻的最佳估计值。

于是迭代也有了。

这就是卡尔曼滤波。

作者：Kent Zeng
链接：https://www.zhihu.com/question/23971601/answer/26254459
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

图片来源及参考文献：http://www.cl.cam.ac.uk/~rmf25/papers/Understanding%20the%20Basis%20of%20the%20Kalman%20Filter.pdf题主如果只是想泛泛理解，Kent Zeng的回答已经非常棒了。我尝试做一个更详细的解答。好了下面进入正题，先从简单的说起：

考虑轨道上的一个小车，无外力作用，它在时刻t的状态向量只与相关：
（状态向量就是描述它的t=0时刻所有状态的向量，比如：
[速度大小5m/s, 速度方向右, 位置坐标0]，反正有了这个向量就可以完全预测t=1时刻小车的状态）

那么根据t=0时刻的初值，理论上我们可以求出它任意时刻的状态。

当然，实际情况不会这么美好。

这个递推函数可能会受到各种不确定因素的影响（内在的外在的都算，比如刮风下雨地震，小车结构不紧密，轮子不圆等等）导致并不能精确标识小车实际的状态。

我们假设每个状态分量受到的不确定因素都服从正态分布。

现在仅对小车的位置进行估计
请看下图：t=0时小车的位置服从红色的正态分布。

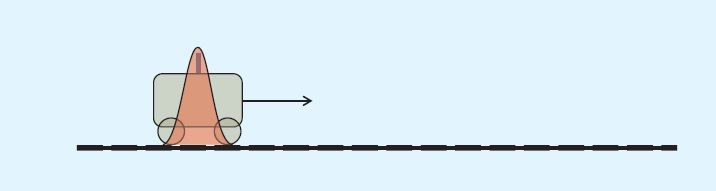
根据小车的这个位置，我们可以预测出t=1时刻它的位置：

分布变“胖”了，这很好理解——因为在递推的过程中又加了一层噪声，所以不确定度变大了。为了避免纯估计带来的偏差，我们在t=1时刻对小车的位置坐标进行一次雷达测量，当然雷达对小车距离的测量也会受到种种因素的影响，于是测量结果告诉我们，小车t=1时的位置服从蓝色分布：

 

好了，现在我们得到两个不同的结果。前面有人提过加权，Kalman老先生的牛逼之处就在于找到了相应权值，使红蓝分布合并为下图这个绿色的正态分布（啰嗦一句，这个绿色分布均值位置在红蓝均值间的比例称为Kalman增益(比如下图中近似0.8)，就是各种公式里的K(t)）出处。

你问为什么牛逼？
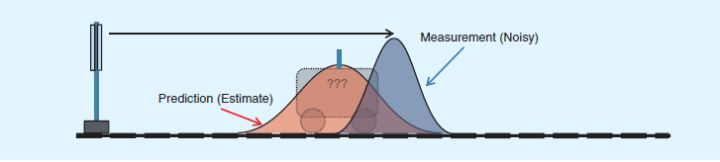
绿色分布不仅保证了在红蓝给定的条件下，小车位于该点的概率最大，而且，而且，它居然还是一个正态分布！正态分布就意味着，可以把它当做初值继续往下算了！这是Kalman滤波能够迭代的关键。最后，把绿色分布当做第一张图中的红色分布对t=2时刻进行预测，算法就可以开始循环往复了。你又要问了，说来说去绿色分布是怎么得出的呢？其实可以通过多种方式推导出来。我们课上讲过的就有最大似然法、Ricatti方程法，以及上面参考文献中提及的直接对高斯密度函数变形的方法，这个不展开说了。另外，由于我只对小车位移这个一维量做了估计，因此Kalman增益是标量，通常情况下它都是一个矩阵。而且如果估计多维量，还应该引入协方差矩阵的迭代，我也没有提到。如果楼主有兴趣，把我提及那篇参考文献吃透，就明白了。Kalman滤波算法的本质就是利用两个正态分布的融合仍是正态分布这一特性进行迭代而已。

作者：肖畅
链接：https://www.zhihu.com/question/23971601/answer/46480923
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。