12.2 ROS NavFn全局规划源码解读_2
博客转载:https://blog.csdn.net/Neo11111/article/details/104645228
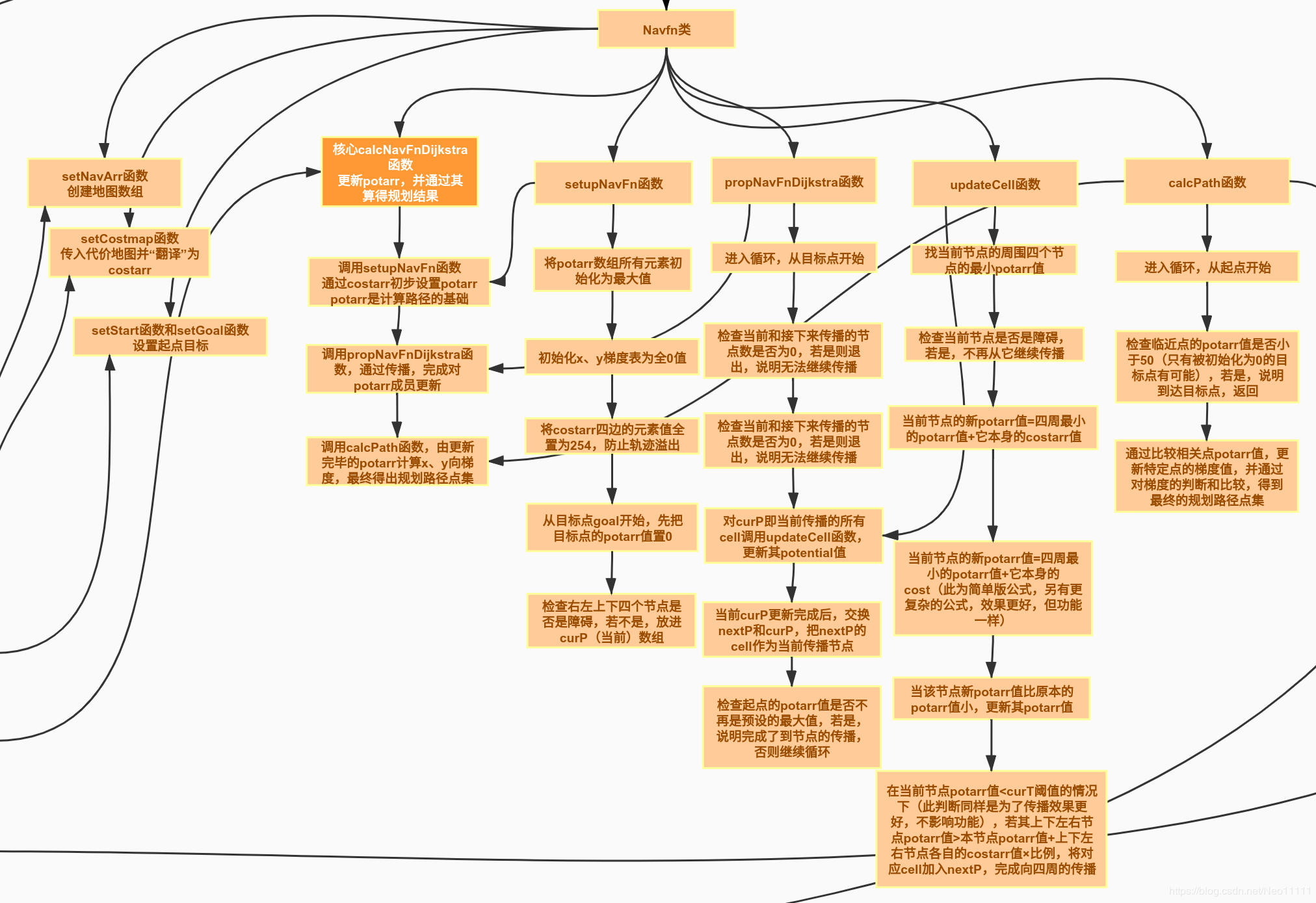
全局规划中使用Dijkstra算法进行实际计算的部分在NavFn类里完成,它通过传入的costmap来设置costarr数组,再通过costarr数组对存储地图上所有cell点Potential值的potarr数组进行更新,并通过potarr数组来计算梯度gradX和gradY,通过迭代比较,最终得到一条完整的全局规划路径。
【相关文件】
- navfn/src/navfn_ros.cpp
- navfn/src/navfn.cpp
本篇记录对navfn.cpp中定义的NavFn类的阅读和理解。
【代码分析】
navfn.cpp
–目录–
NavFn::setCostmap | 将Costmap“翻译”成costarr
NavFn::calcNavFnDijkstra | Dijkstra计算主体部分
NavFn::setupNavFn | 处理costarr,初始化potarr、gradx、grady
NavFn::propNavFnDijkstra | 更新potarr数组
NavFn::updateCell | 单点Potential传播
NavFn::calcPath | 路径生成
<1> NavFn::setCostmap
用指针指向数组costarr,COSTTYPE宏定义为unsigned char,即ROS中使用的地图Costmap2D中用于储存地图数据的成员类型。
void NavFn::setCostmap(const COSTTYPE *cmap, bool isROS, bool allow_unknown) { //全局规划用到的地图costarr COSTTYPE *cm = costarr;
接下来在地图的长宽范围内进行迭代:
① 若当前cell在costmap上的值 < COST_OBS_ROS(253),即非致命障碍物(障碍物附近),重新将其赋值为COST_NEUTRAL(50)+当前cell在costmap上的值×比例0.8,最高253;
② 若当前cell在costmap上的值 == COST_UNKNOWN_ROS(255),即未知区域,赋值为253;
③ 若当前cell在costmap上的值 == COST_OBS(254),即致命障碍物(障碍物本身),值仍为254。
这样,将获得数组costarr,元素范围在50~254之间。
if (isROS)//ROS map { for (int i=0; i<ny; i++) { //k值记录二重迭代的次数 int k=i*nx; //cmap指向costmap元素,cm指向costarr for (int j=0; j<nx; j++, k++, cmap++, cm++) { //默认最小权重值为COST_NEUTRAL=50,最大权重值为COST_OBS=254 //注:最小权重值即行走单个free(无障碍物影响)栅格所付出的权重代价 //最大权重值即行走单个障碍物栅格所付出的权重代价 *cm = COST_OBS; int v = *cmap; //若当前cell的代价小于障碍物类型(253),实际上253是膨胀型障碍 if (v < COST_OBS_ROS) { //重新将其赋值为50+cost地图上的障碍物值×比例0.8 v = COST_NEUTRAL+COST_FACTOR*v; //若值>=COST_OBS(254,致命层障碍) if (v >= COST_OBS) //统一设置为253,确保不要超出范围 v = COST_OBS-1; //赋值给当前全局规划要使用的地图costarr *cm = v; } //若当前cell的值为COST_UNKNOWN_ROS(255),未知区域 else if(v == COST_UNKNOWN_ROS && allow_unknown) { //统一设置为253 v = COST_OBS-1; *cm = v; } } } }
当地图类型是其他类型(如PGM),也执行同样的“翻译”工作,设置costarr数组。
else { for (int i=0; i<ny; i++) { int k=i*nx; for (int j=0; j<nx; j++, k++, cmap++, cm++) { *cm = COST_OBS; if (i<7 || i > ny-8 || j<7 || j > nx-8) continue; //避免处理边界cell int v = *cmap; if (v < COST_OBS_ROS) { v = COST_NEUTRAL+COST_FACTOR*v; if (v >= COST_OBS) v = COST_OBS-1; *cm = v; } else if(v == COST_UNKNOWN_ROS) { v = COST_OBS-1; *cm = v; } } } } }
<2> NavFn::calcNavFnDijkstra
这个函数内完成了整个路径计算的流程,顺序调用了几个子部分的函数。
bool NavFn::calcNavFnDijkstra(bool atStart) { #if 0 static char costmap_filename[1000]; static int file_number = 0; snprintf( costmap_filename, 1000, "navfn-dijkstra-costmap-%04d", file_number++ ); savemap( costmap_filename ); #endif //重新设置势场矩阵potarr的值、设置costarr的边际值、设置目标在costarr中的值为0,对四周cell进行处理,记录costarr中障碍物cell数 setupNavFn(true); // calculate the nav fn and path propNavFnDijkstra(std::max(nx*ny/20,nx+ny),atStart); // path int len = calcPath(nx*ny/2); if (len > 0) // found plan { ROS_DEBUG("[NavFn] Path found, %d steps\n", len); return true; } else { ROS_DEBUG("[NavFn] No path found\n"); return false; } }
<3> NavFn::setupNavFn
该函数对“翻译”生成的costarr数组进行了边际设置等处理,并初始化了potarr数组和梯度数组gradx、grady。下面先循环初始化potarr矩阵元素全部为最大值POT_HIGH,并初始化梯度表初始值全部为0.0。
void NavFn::setupNavFn(bool keepit) { //重新设置势场矩阵potarr的值 for (int i=0; i<ns; i++) { //将代价值表初始化为最大值,默认起点到所有点的行走代价值都为最大 potarr[i] = POT_HIGH; if (!keepit) costarr[i] = COST_NEUTRAL; //初始化x,y方向的梯度表 gradx[i] = grady[i] = 0.0; }
接下来设置costarr的四条边的cell的值为COST_OBS(致命层254),封闭地图四周,以防产生边界以外的轨迹。
COSTTYPE *pc; pc = costarr; //costarr第一行全部设置为COST_OBS(致命层254) for (int i=0; i<nx; i++) *pc++ = COST_OBS; //costarr最后一行全部设置为COST_OBS(致命层254) pc = costarr + (ny-1)*nx; for (int i=0; i<nx; i++) *pc++ = COST_OBS; pc = costarr; //costarr第一列全部设置为COST_OBS(致命层254) for (int i=0; i<ny; i++, pc+=nx) *pc = COST_OBS; pc = costarr + nx - 1; //costarr最后一列全部设置为COST_OBS(致命层254) for (int i=0; i<ny; i++, pc+=nx) *pc = COST_OBS;
初始化一些用于迭代更新potarr的数据,并初始化pending数组为全0,设置所有的cell状态都为非等待状态。
//有限缓冲器 curT = COST_OBS;//当前传播阈值 curP = pb1; //当前用于传播的cell索引数组 curPe = 0;//当前用于传播的cell的数量 nextP = pb2;//用于下个传播过程的cell索引数组 nextPe = 0;//用于下个传播过程的cell的数量 overP = pb3;//传播界限外的cell索引数组 overPe = 0;//传播界限外的cell的数量 memset(pending, 0, ns*sizeof(bool));
接下来设置目标goal在potarr中的值为0,并把它四周非障碍物的cell加入curP数组(当前传播cell)中,为下一步的Potential值在整张地图上的传播做准备。
//k为目标cell的索引 int k = goal[0] + goal[1]*nx; //设置costarr的索引k(目标)的元素值为0,并对它四周的cell在pending[]中进行标记“等待状态”,并把索引存放入curP数组 initCost(k,0); //更新nobs,记录costarr中的致命障碍物cell的数量 pc = costarr; int ntot = 0; for (int i=0; i<ns; i++, pc++) { if (*pc >= COST_OBS) ntot++; } nobs = ntot; }
<4> NavFn::propNavFnDijkstra
这个函数以目标点(Potential值已初始化为0)为起点,向整张地图的cell传播,填充potarr数组,直到找到起始点为止,potarr数组的数据能够反映“走了多远”和“附近的障碍情况”,为最后的路径计算提供了依据。
bool NavFn::propNavFnDijkstra(int cycles, bool atStart) { int nwv = 0; //priority block的最大数量 int nc = 0; //priority blocks中的cell数 int cycle = 0; //当前迭代次数 //记录起始位置的索引 int startCell = start[1]*nx + start[0];
循环迭代更新potarr,判断条件:如果当前正在传播和下一步传播的集都为空,那么说明已经无法继续传播,可能有无法越过的障碍或其他情况,退出。
//循环迭代,次数为cycles for (; cycle < cycles; cycle++) { if (curPe == 0 && nextPe == 0) break; // stats nc += curPe; if (curPe > nwv) nwv = curPe; //对pending数组进行设置 int *pb = curP; int i = curPe; while (i-- > 0) pending[*(pb++)] = false;
接下来传播curP,即当前cell,调用的函数为updateCell,它能更新当前cell在potarr数组中的值,并将其四周符合特定条件的点放入nextP或overP,用于下一步的传播。调用完成后,将nextP数组中的cell传递给curP,继续上述传播,若nextP没有cell可以用来传播,则引入overP中的cell。
nextP和overP都来自从目标点开始传播的四周的cell,区别在于它们的“父cell”的pot值是否达到阈值curT,没达到则放入nextP,达到则放入overP。
在阅读其他博主的博客学习这部分时发现,设置一个阈值来区分nextP和overP的传播先后顺序,结果是以目标点为圆心向外圆形传播,而不设阈值区分,则是以目标点为中心向外呈菱形传播,显然前者更合理。
// 处理curP pb = curP; i = curPe; while (i-- > 0) updateCell(*pb++); if (displayInt > 0 && (cycle % displayInt) == 0) displayFn(this); // swap priority blocks curP <=> nextP curPe = nextPe; nextPe = 0; pb = curP; // swap buffers curP = nextP; nextP = pb; // see if we're done with this priority level if (curPe == 0) { curT += priInc; // increment priority threshold curPe = overPe; // set current to overflow block overPe = 0; pb = curP; // swap buffers curP = overP; overP = pb; }
在从目标点向全地图传播的过程中检查,当起点的Potential值不再是被初始化的无穷大,而是有一个实际的值时,说明到达了起点,传播停止。
<5> NavFn::updateCell
updateCell用于更新单个cell的Potential值,先获取当前cell四周邻点的potarr值,并取最小的值存入ta。
inline void NavFn::updateCell(int n) { // get neighbors float u,d,l,r; l = potarr[n-1]; r = potarr[n+1]; u = potarr[n-nx]; d = potarr[n+nx]; // ROS_INFO("[Update] c: %0.1f l: %0.1f r: %0.1f u: %0.1f d: %0.1f\n", // potarr[n], l, r, u, d); // ROS_INFO("[Update] cost: %d\n", costarr[n]); // find lowest, and its lowest neighbor float ta, tc; if (l<r) tc=l; else tc=r; if (u<d) ta=u; else ta=d;
下面执行一个判断,只有当当前cell不是致命障碍物时,才由它向四周传播,否则到它后停止,不传播。
// do planar wave update if (costarr[n] < COST_OBS) // don't propagate into obstacles { float hf = (float)costarr[n]; // traversability factor float dc = tc-ta; // relative cost between ta,tc if (dc < 0) // ta is lowest { dc = -dc; ta = tc; }
在计算当前点Potential值时,有两种情况,即需要对“左右邻点最小pot值与上下邻点最小pot值之差的绝对值”和“当前cell的costarr值”比较,有pot = ta+hf和另一个更复杂的公式,这两个公式的功能相同,但效果有区别,区别也是前面提到过的“圆形传播”和“菱形传播”,后者能够产生效果更好的菱形传播。
只有当前cell的Potential计算值<原本的Potential值,才更新,这意味着从目标点开始,它的Potential值被初始化为0,不会被更新,接下来传播到它的四个邻点,才会开始更新他们的Potential值。
// calculate new potential float pot; if (dc >= hf) // if too large, use ta-only update pot = ta+hf; else // two-neighbor interpolation update { // use quadratic approximation // might speed this up through table lookup, but still have to // do the divide float d = dc/hf; float v = -0.2301*d*d + 0.5307*d + 0.7040; pot = ta + hf*v; } // ROS_INFO("[Update] new pot: %d\n", costarr[n]); // now add affected neighbors to priority blocks if (pot < potarr[n]) { float le = INVSQRT2*(float)costarr[n-1]; float re = INVSQRT2*(float)costarr[n+1]; float ue = INVSQRT2*(float)costarr[n-nx]; float de = INVSQRT2*(float)costarr[n+nx]; potarr[n] = pot;
为便于理解,这里分析第一个公式,当前点Potential值=四周最小的Potential值+当前点cost值。这说明,从目标点(Potential=0)向外传播时,它四周的可行cell的Potential值会变成0+cost,可以假设他们的cost都是50,那么它们的Potential值都被更新为50(因为初始值无限大,故会被迭代)。第二轮次的传播中,假设邻点的邻点cost也为50,那么它们的Potential值将被更新为100。这种传播过程中cost的累加造成Potential值的上升能够反映离目标点的远近。
并且,cost大小与cell离障碍物的远近对应,更大的cost对应更大的Potential,并且障碍物点不更新Potential,使得其值停留在无限大,故Potential值的大小也能反映点与障碍物的接近程度。
最后,将临近cell放入nextP或overP,供下次迭代使用。
if (pot < curT) // low-cost buffer block { if (l > pot+le) push_next(n-1); if (r > pot+re) push_next(n+1); if (u > pot+ue) push_next(n-nx); if (d > pot+de) push_next(n+nx); } else // overflow block { if (l > pot+le) push_over(n-1); if (r > pot+re) push_over(n+1); if (u > pot+ue) push_over(n-nx); if (d > pot+de) push_over(n+nx); } } } }
假设一张简单的costmap图如下,右下角紫色格子为目标点,左上角绿色格子为起点:
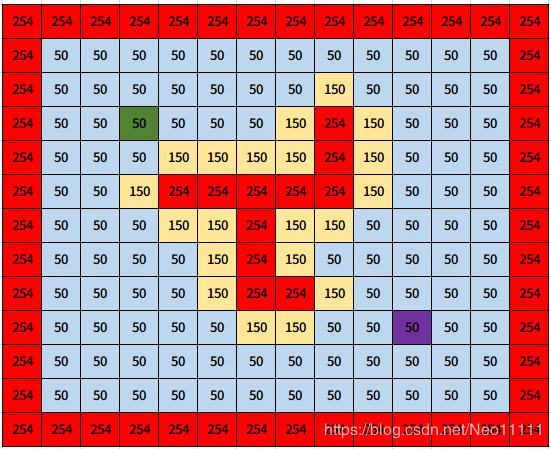
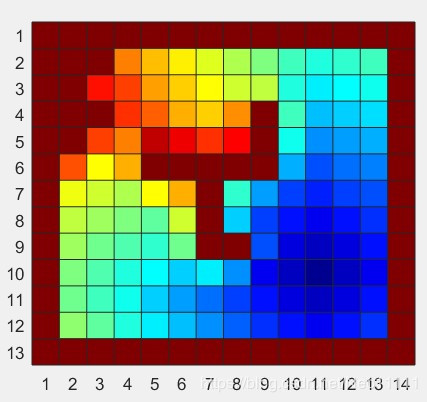
由它生成的potarr图示如下,蓝色为小值,红色为大值,暗红色为无穷大:
<5> NavFn::calcPath
该函数负责在potarr数组的基础上选取一些cell点来生成最终的全局规划路径,从起点开始沿着最优行走代价值梯度下降的方向寻找到目标点的最优轨迹。
int NavFn::calcPath(int n, int *st) { // test write //savemap("test"); // check path arrays if (npathbuf < n) { if (pathx) delete [] pathx; if (pathy) delete [] pathy; pathx = new float[n]; pathy = new float[n]; npathbuf = n; } // set up start position at cell // st is always upper left corner for 4-point bilinear interpolation if (st == NULL) st = start;//st指向起点 int stc = st[1]*nx + st[0];//stc记录起点索引 // set up offset float dx=0; float dy=0; npath = 0;//路径点索引 // go for <n> cycles at most for (int i=0; i<n; i++) { // check if near goal int nearest_point=std::max(0,std::min(nx*ny-1,stc+(int)round(dx)+(int)(nx*round(dy)))); if (potarr[nearest_point] < COST_NEUTRAL) { pathx[npath] = (float)goal[0]; pathy[npath] = (float)goal[1]; return ++npath; // done! } if (stc < nx || stc > ns-nx) //在第一行或最后一行,即超出边界 { ROS_DEBUG("[PathCalc] Out of bounds"); return 0; } //添加至路径点 pathx[npath] = stc%nx + dx;//x向索引 pathy[npath] = stc/nx + dy;//y向索引 npath++; //震荡检测,某一步和上上一步的位置是否一样 bool oscillation_detected = false; if( npath > 2 && pathx[npath-1] == pathx[npath-3] && pathy[npath-1] == pathy[npath-3] ) { ROS_DEBUG("[PathCalc] oscillation detected, attempting fix."); oscillation_detected = true; } int stcnx = stc+nx; //当前点下方的点的索引 int stcpx = stc-nx; //当前点上方的点的索引 //检查当前到达节点的周边的8个节点是否有障碍物代价值,如果有的话,则直接将stc指向这8个节点中potential值最低的节点 if (potarr[stc] >= POT_HIGH || potarr[stc+1] >= POT_HIGH || potarr[stc-1] >= POT_HIGH || potarr[stcnx] >= POT_HIGH || potarr[stcnx+1] >= POT_HIGH || potarr[stcnx-1] >= POT_HIGH || potarr[stcpx] >= POT_HIGH || potarr[stcpx+1] >= POT_HIGH || potarr[stcpx-1] >= POT_HIGH || oscillation_detected) { ROS_DEBUG("[Path] Pot fn boundary, following grid (%0.1f/%d)", potarr[stc], npath); //检查八个邻点中的最小值 int minc = stc; int minp = potarr[stc]; int st = stcpx - 1; //从左上角邻点开始 if (potarr[st] < minp) {minp = potarr[st]; minc = st; }//记录最小Potential的索引minc和值minp st++; //上方邻点 if (potarr[st] < minp) {minp = potarr[st]; minc = st; } st++; //右上方邻点 if (potarr[st] < minp) {minp = potarr[st]; minc = st; } //左邻点 st = stc-1; if (potarr[st] < minp) {minp = potarr[st]; minc = st; } //右邻点 st = stc+1; if (potarr[st] < minp) {minp = potarr[st]; minc = st; } //左下方邻点 st = stcnx-1; if (potarr[st] < minp) {minp = potarr[st]; minc = st; } st++; //下方邻点 if (potarr[st] < minp) {minp = potarr[st]; minc = st; } st++; //右下方邻点 if (potarr[st] < minp) {minp = potarr[st]; minc = st; } stc = minc; dx = 0; dy = 0; ROS_DEBUG("[Path] Pot: %0.1f pos: %0.1f,%0.1f", potarr[stc], pathx[npath-1], pathy[npath-1]); if (potarr[stc] >= POT_HIGH) { ROS_DEBUG("[PathCalc] No path found, high potential"); //savemap("navfn_highpot"); return 0; } } //如果有好的梯度,则直接计算梯度,并沿着梯度方向查找下一个节点 else //当周围八个邻点没有障碍物 { // get grad at four positions near cell gradCell(stc);//该点 gradCell(stc+1);//该点右侧点 gradCell(stcnx);//该点下方点 gradCell(stcnx+1);//该点右下方点 // get interpolated gradient float x1 = (1.0-dx)*gradx[stc] + dx*gradx[stc+1]; float x2 = (1.0-dx)*gradx[stcnx] + dx*gradx[stcnx+1]; float x = (1.0-dy)*x1 + dy*x2; // interpolated x float y1 = (1.0-dx)*grady[stc] + dx*grady[stc+1]; float y2 = (1.0-dx)*grady[stcnx] + dx*grady[stcnx+1]; float y = (1.0-dy)*y1 + dy*y2; // interpolated y // show gradients ROS_DEBUG("[Path] %0.2f,%0.2f %0.2f,%0.2f %0.2f,%0.2f %0.2f,%0.2f; final x=%.3f, y=%.3f\n", gradx[stc], grady[stc], gradx[stc+1], grady[stc+1], gradx[stcnx], grady[stcnx], gradx[stcnx+1], grady[stcnx+1], x, y); // check for zero gradient, failed if (x == 0.0 && y == 0.0) { ROS_DEBUG("[PathCalc] Zero gradient"); return 0; } // move in the right direction float ss = pathStep/hypot(x, y); dx += x*ss; dy += y*ss; // check for overflow if (dx > 1.0) { stc++; dx -= 1.0; } if (dx < -1.0) { stc--; dx += 1.0; } if (dy > 1.0) { stc+=nx; dy -= 1.0; } if (dy < -1.0) { stc-=nx; dy += 1.0; } } // ROS_INFO("[Path] Pot: %0.1f grad: %0.1f,%0.1f pos: %0.1f,%0.1f\n", // potarr[stc], x, y, pathx[npath-1], pathy[npath-1]); } // return npath; // out of cycles, return failure ROS_DEBUG("[PathCalc] No path found, path too long"); //savemap("navfn_pathlong"); return 0; // out of cycles, return failure }
以刚刚的简单costmap和potarr为例,由它生成的梯度数组gradx和grady如下:
gradx:
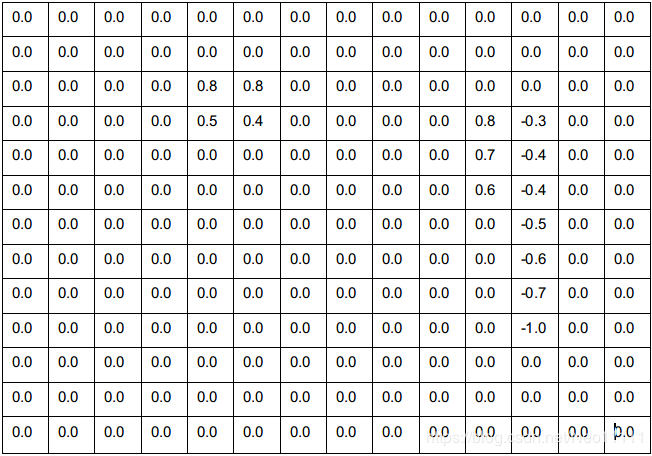
grady:

最终生成的路径(左下方路径):
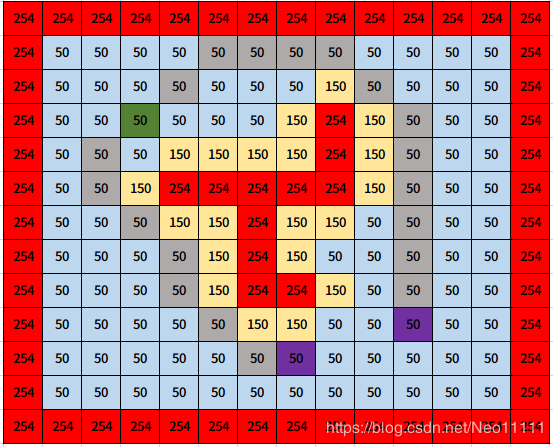
将目标点更换为右边的紫色点,重新进行规划,得右边的路径。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号