3D数学 ---- 矩阵的更多知识(2)
矩阵的逆
另外一种重要的矩阵运算是矩阵的求逆,这个运算只能用于方阵。
运算法则
方阵M的逆,记作M-1,也是一个矩阵。当M与M-1相乘时,结果是单位矩阵。表示为公式9.6的形式:
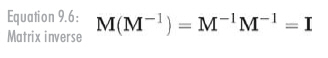
并非所有的矩阵都有逆。一个明显的例子是若矩阵的某一行或列上的元素都为0,用任何矩阵乘以该矩阵,结果都是一个零矩阵。如果一个矩阵有逆矩阵,那么称它为可逆的或非奇异的。如果一个矩阵没有逆矩阵,则称它为不可逆的或奇异矩阵。奇异矩阵的行列式为0,非奇异矩阵的行列式不为0,所以检测行列式的值是判断矩阵是否可逆的有效方法。此外,对于任意可逆矩阵M,当且仅当v=0时,vM=0。
M的”标准伴随矩阵“记作”adjM“,定义为M的代数余子式矩阵的转置矩阵。下面是一个例子,考虑前面给出的3x3阶矩阵M:
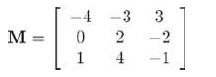
计算M的代数余子式矩阵:
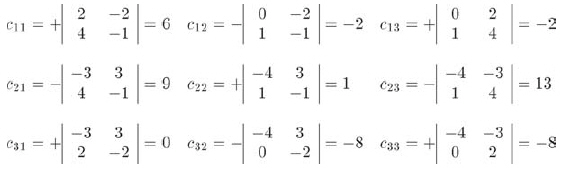
M的标准伴随矩阵是代数余子式矩阵的转置:
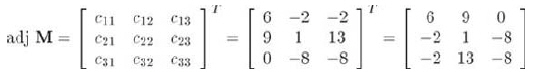
一旦有了标准伴随矩阵,通过除以M的行列式,就能计算矩阵的逆。
其表示如公式9.7所示:

例如为了求得上面矩阵的逆,有:
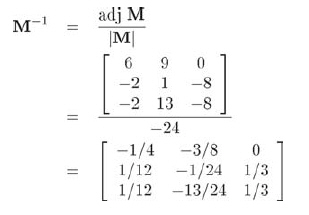
当然还有其他方法可以用来计算矩阵的逆,比如高斯消元法。很多线性代数书都断定该方法更适合在计算机上实现,因为它所使用的代数运算较少,这种说法其实是不正确的。对于大矩阵或某些特殊矩阵来说,这也许是对的。然而,对于低阶矩阵,比如几何应用中常见的那些低阶矩阵,标准伴随矩阵可能更快一些。因为可以为标准伴随矩阵提供无分支(branchless)实现,这种实现方法在当今的超标量体系结构和专用向量处理器上会更快一些。
矩阵的逆的重要性质:

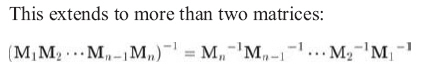
几何解释
矩阵的逆在几何上非常有用,因为它使得我们可以计算变换的”反向“或”相反“变换 ---- 能”撤销“原变换的变换。所以,如果向量v用矩阵M来进行变换,接着用M的逆M-1进行变换,将会得到原向量。这很容易通过代数方法验证:
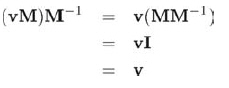
我最擅长从零开始创造世界,所以从来不怕失败,它最多也就让我一无所有。




