凸优化算法之牛顿法

原理

对于求方程解问题，假设有函数 f  :R->R，我们希望找到满足 f(θ)=0 的θ值. 这里θ是实数. 

牛顿方法执行下面的更新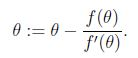

 

求解过程如图所示

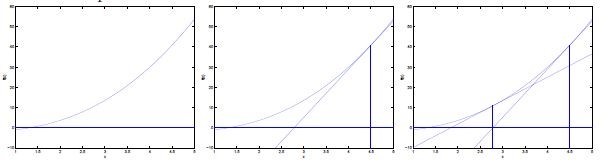
简单的来说就是通过求当前点的导数得到下一个点.用到的性质是导数值等于该点切线和横轴夹角的正切值

利用凸函数的性质，最值所在点 l'（θ）=0  令f(θ)=l'(θ)

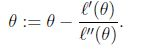
牛顿方法的一般化： 
如果θ是一个向量，那么： 

 

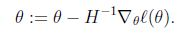
H称为海森矩阵(Hessian matrix),是一个n*n的矩阵，n是特征量的个数，并且

牛顿方法的收敛速度比批处理梯度下降快很多，很少次的迭代就能够非常接近最小值了；但是当n很大时，每次迭代求海森矩阵和逆代价是很大的。

牛顿法是二阶收敛，梯度下降法是一阶收敛的，所以牛顿法看得更远，收敛更快。牛顿法的路径更符合最优路径。对于二阶凸函数能够一步到达。

实际中常常先用梯度下降法，在离得比较近时使用牛顿法；由于牛顿法需要每次更新海森矩阵，所以使用拟牛顿法。

---

举例

求解问题   f(x₁,x₂) = -x₁⁴ - 2x₂⁴ + 2x₁x₂ + 2x₂ + 6

▽_x1f =-4x₁³+2x₂

▽_x2f = 2x₁-8x₂³+2

Hessian = [ -12x₁², 2; 2, -24x₂²]

迭代次数计数

        {

[x₁ ; x₂ ] = [x₁ ; x₂ ] -Hessian 点乘  [▽_x1f ; ▽_x2f ]

}

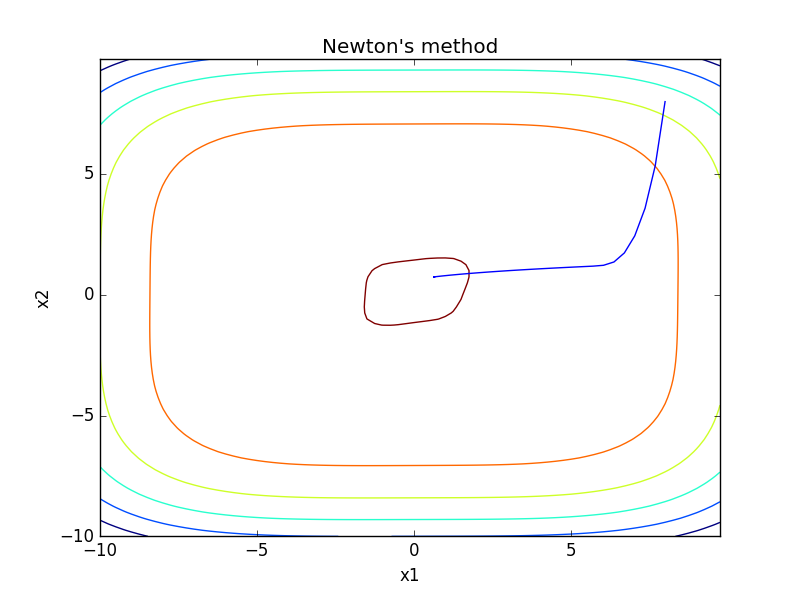
# -*- coding: utf-8 -*-
"""
Created on Wed Apr 12 23:56:25 2017
@author: LoveDMR
牛顿方法
"""
import numpy as np
import matplotlib.pyplot as plt
delta = 0.25
x1 = np.arange( -10 , 10 , delta )
x2 = np.arange( -10 , 10 , delta )
X1 , X2 = np.meshgrid( x1 , x2 )
Y = 2*X1*X2+2*X2-X1**4-2*X2**4 + 6
plt.figure()
bg_fig = plt.contour(X1,X2,Y)
theta = np.array([8,8])
a , b = [] , []
a.append(theta[0])
b.append(theta[1])
H = np.array([[2,3],[3,10]])
Hi = np.linalg.inv(H)
for i in xrange(1,50):
    t = np.array([theta[0]**3*(-4)+2*theta[1]**2 , (-8)*theta[1]**3+2*theta[0]+2])
    H = np.array([[(-12)*theta[0]**3,2],[2,(-24)*theta[1]**2]])
    Hi = np.linalg.inv(H)
    theta = theta - np.dot( Hi ,t )
    a.append(theta[0])
    b.append(theta[1])
plt.plot(a , b)
plt.title( "Newton's method" )
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()