看动画学算法之:双向队列dequeue
简介
dequeue指的是双向队列,可以分别从队列的头部插入和获取数据,也可以从队列的尾部插入和获取数据。
本文将会介绍一下怎么创建dequeue和dequeue的一些基本操作。
双向队列的实现
和普通队列项目,双向队列可以分别在头部和尾部进行插入和删除工作,所以一个dequeue需要实现这4个方法:
- insertFront(): 从dequeue头部插入数据
- insertLast(): 从dequeue尾部插入数据
- deleteFront(): 从dequeue头部删除数据
- deleteLast(): 从dequeue尾部删除数据
同样的我们也需要一个head和一个rear来指向队列的头部和尾部节点。
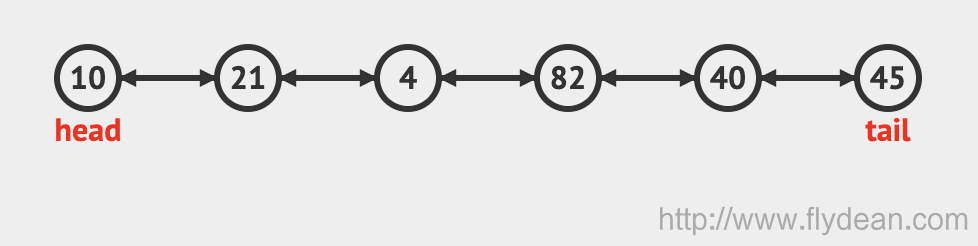
也就是说实现了这四个方法的队列就是双向队列。我们不管它内部是怎么实现的。
接下来我们来直观的感受一下dequeue的插入和删除操作:
- 在头部插入
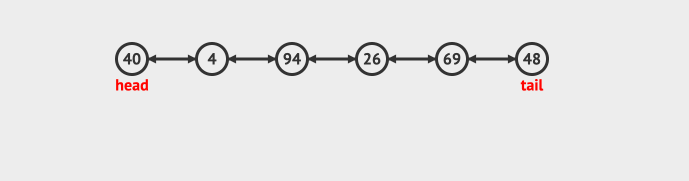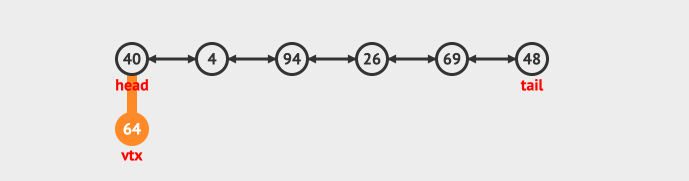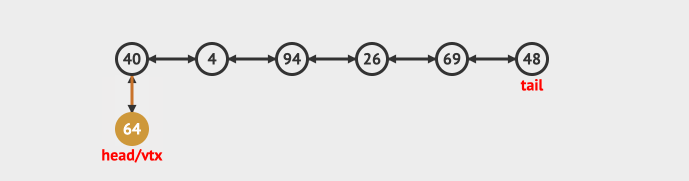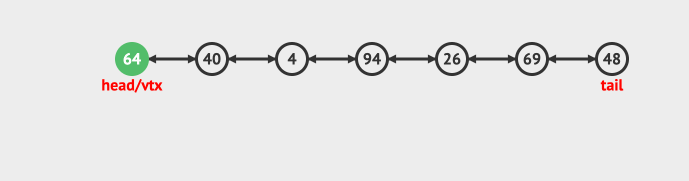
- 在尾部插入
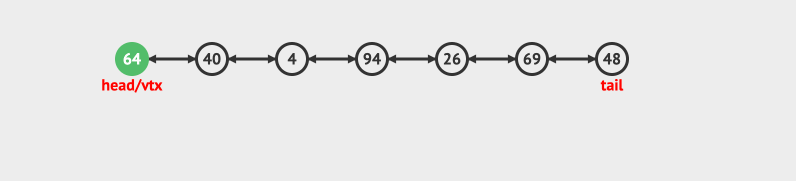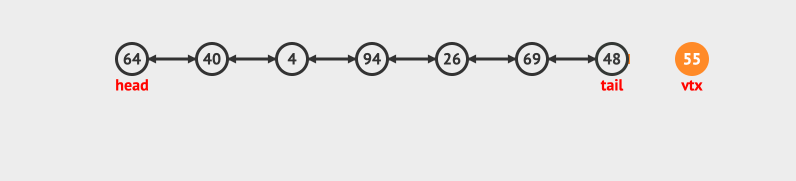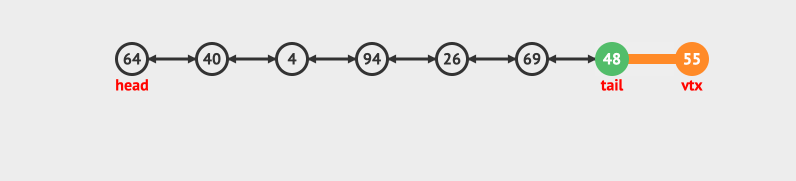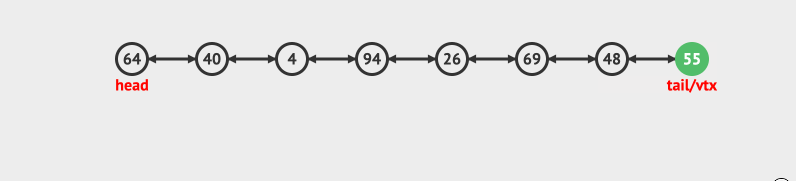
- 在头部删除
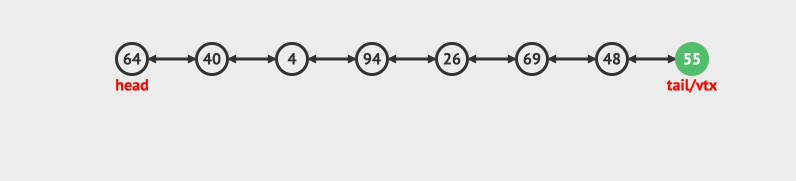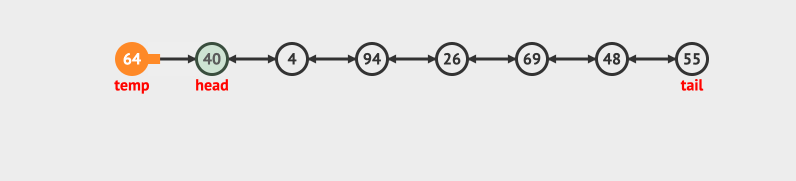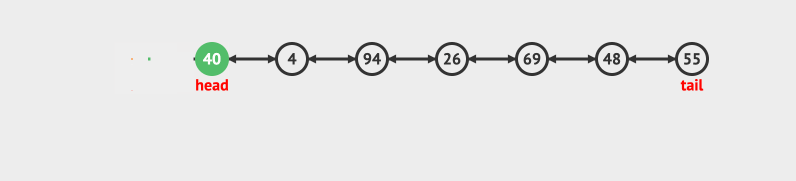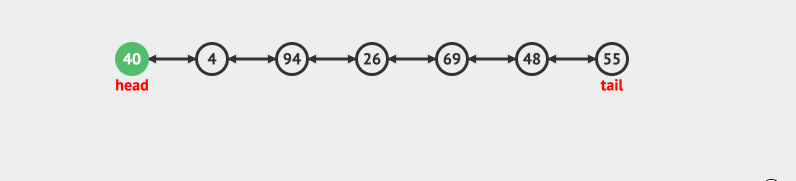
- 在尾部删除
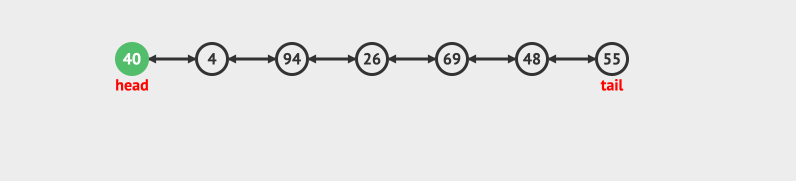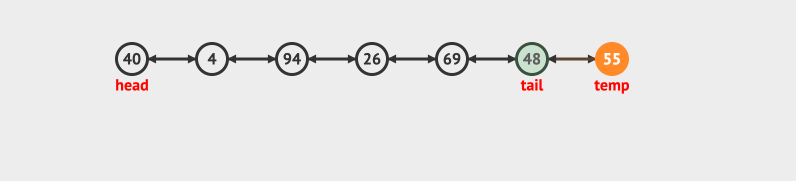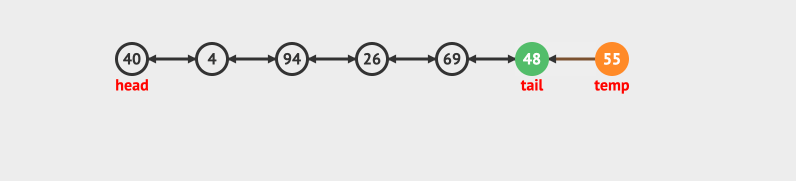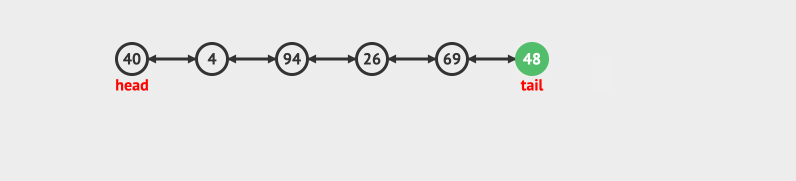
双向队列也可以有很多种实现方式,比如循环数组和链表。
双向队列的数组实现
因为数组本身已经有前后关系,也就是说知道head可以拿到它后面一个数据,知道rear也可以拿到它前面一个数据。
所以数组的实现中,存储head和rear的index值已经够了。
我们只需要添加向头部插入数据和向尾部删除数据的方法即可:
//从头部入队列
public void insertFront(int data){
if(isFull()){
System.out.println("Queue is full");
}else{
//从头部插入ArrayDeque
head = (head + capacity - 1) % capacity;
array[head]= data;
//如果插入之前队列为空,将real指向head
if(rear == -1 ){
rear = head;
}
}
}
//从尾部取数据
public int deleteLast(){
int data;
if(isEmpty()){
System.out.println("Queue is empty");
return -1;
}else{
data= array[rear];
//如果只有一个元素,则重置head和real
if(head == rear){
head= -1;
rear = -1;
}else{
rear = (rear + capacity - 1)%capacity;
}
return data;
}
}
双向队列的动态数组实现
动态数组可以动态改变数组大小,这里我们使用倍增的方式来扩展数组。
看下扩展方法怎么实现:
//因为是循环数组,这里不能做简单的数组拷贝
private void extendQueue(){
int newCapacity= capacity*2;
int[] newArray= new int[newCapacity];
//先全部拷贝
System.arraycopy(array,0,newArray,0,array.length);
//如果rear<head,表示已经进行循环了,需要将0-head之间的数据置空,并将数据拷贝到新数组的相应位置
if(rear < head){
for(int i=0; i< head; i++){
//重置0-head的数据
newArray[i]= -1;
//拷贝到新的位置
newArray[i+capacity]=array[i];
}
//重置rear的位置
rear = rear +capacity;
//重置capacity和array
capacity=newCapacity;
array=newArray;
}
}
因为是循环数组,这里不能做简单的数组拷贝,我们需要判断rear和head的位置来判断是否进入到了循环结构。
如果进入到了循环结构,我们需要重置相应的字段数据,并拷贝到新数组中。
向头部插入数据和向尾部删除数据的方法和基本队列的实现是一致的,这里就不列出来了。
双向队列的链表实现
如果使用链表来实现双向队列会有什么问题呢?
在头部插入和在尾部插入都可以快速定位到目标节点。但是我们考虑一下尾部删除的问题。
尾部删除我们需要找到尾部节点的前一个节点,将这个节点置位rear节点。这就需要我们能够通过rear节点找到它的前一个节点。
所以基本的链表已经满足不了我们的需求了。 这里我们需要使用双向链表。
public class LinkedListDeQueue {
//head节点
private Node headNode;
//rear节点
private Node rearNode;
class Node {
int data;
Node next;
Node prev;
//Node的构造函数
Node(int d) {
data = d;
}
}
public boolean isEmpty(){
return headNode==null;
}
//从队尾插入
public void insertLast(int data){
Node newNode= new Node(data);
//将rearNode的next指向新插入的节点
if(rearNode !=null){
rearNode.next=newNode;
newNode.prev=rearNode;
}
rearNode=newNode;
if(headNode == null){
headNode=newNode;
}
}
//从队首插入
public void insertFront(int data){
if(headNode == null){
headNode= new Node(data);
}else{
Node newNode= new Node(data);
newNode.next= headNode;
headNode.prev= newNode;
headNode= newNode;
}
}
//从队首删除
public int deleteFront(){
int data;
if(isEmpty()){
System.out.println("Queue is empty");
return -1;
}else{
data=headNode.data;
headNode=headNode.next;
headNode.prev=null;
}
return data;
}
//从队尾删除
public int deleteLast(){
int data;
if(isEmpty()){
System.out.println("Queue is empty");
return -1;
}else{
data=rearNode.data;
rearNode=rearNode.prev;
rearNode.next=null;
}
return data;
}
}
双向链表中的每一个节点都有next和prev两个指针。通过这两个指针,我们可以快速定位到他们的后一个节点和前一个节点。
双向链表的时间复杂度
上面的3种实现的enQueue和deQueue方法,基本上都可以立马定位到要入队列或者出队列的位置,所以他们的时间复杂度是O(1)。
本文的代码地址:
本文已收录于 http://www.flydean.com/13-algorithm-dequeue/
最通俗的解读,最深刻的干货,最简洁的教程,众多你不知道的小技巧等你来发现!
欢迎关注我的公众号:「程序那些事」,懂技术,更懂你!





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步