看动画学算法之:队列queue
简介
队列Queue是一个非常常见的数据结构,所谓队列就是先进先出的序列结构。
想象一下我们日常的排队买票,只能向队尾插入数据,然后从队头取数据。在大型项目中常用的消息中间件就是一个队列的非常好的实现。
队列的实现
一个队列需要一个enQueue入队列操作和一个DeQueue操作,当然还可以有一些辅助操作,比如isEmpty判断队列是否为空,isFull判断队列是否满员等等。
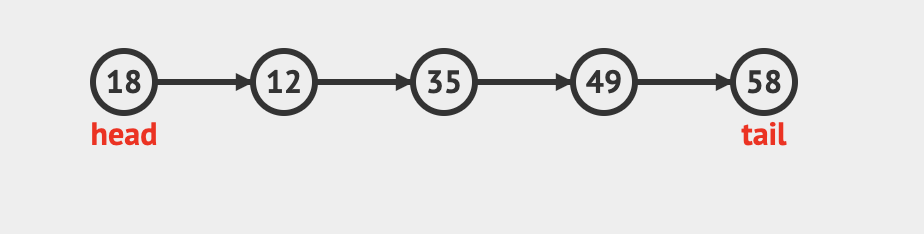
为了实现在队列头和队列尾进行方便的操作,我们需要保存队首和队尾的标记。
先看一下动画,直观的感受一下队列是怎么入队和出队的。
先看入队:
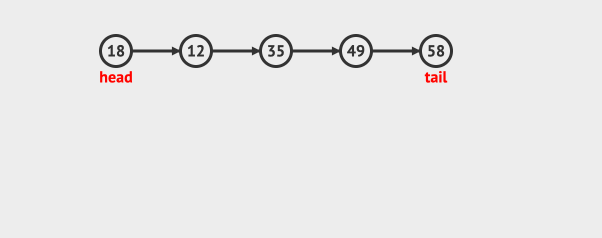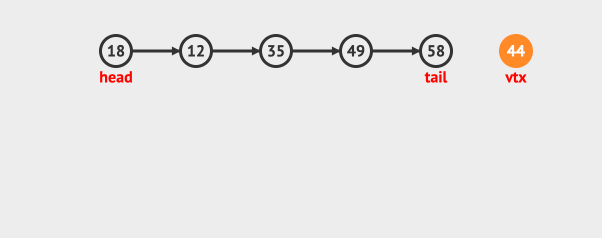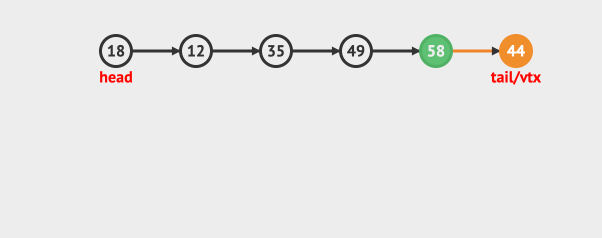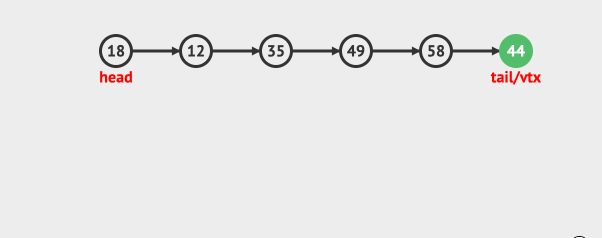
再看出队:
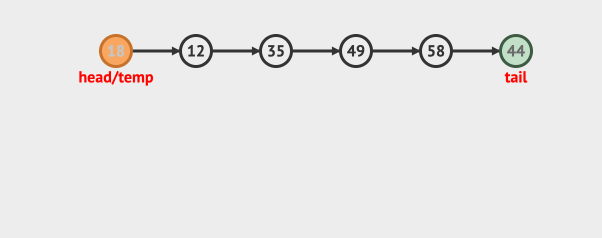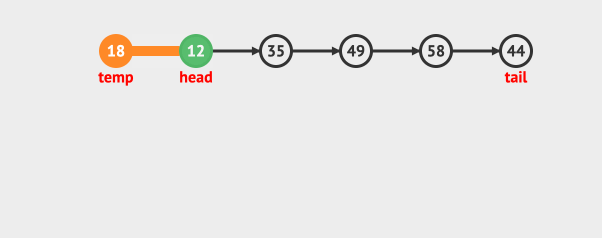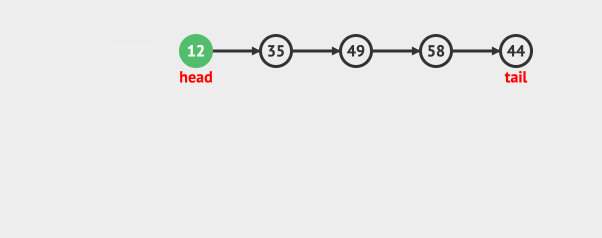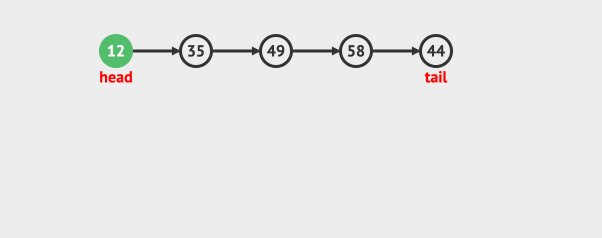
可以看到入队是从队尾入,而出队是从队首出。
队列的数组实现
和栈一样,队列也有很多种实现方式,最基本的可以使用数组或者链表来实现。
先考虑一下使用数组来存储数据的情况。
我们用head表示队首的index,使用rear表示队尾的index。
当队尾不断插入,队首不断取数据的情况下,很有可能出现下面的情况:
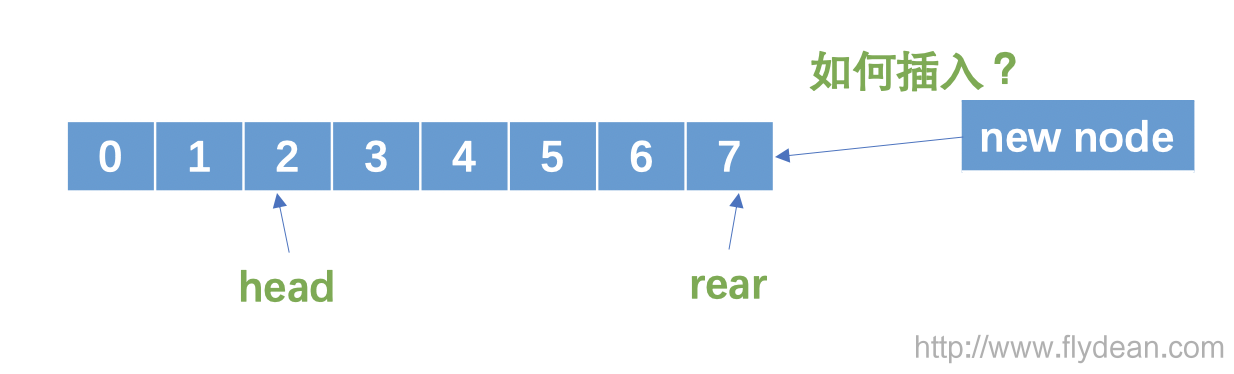
上面图中,head的index已经是2了,rear已经到了数组的最后面,再往数组里面插数据应该怎么插入呢?
如果再往rear后面插入数据,head前面的两个空间就浪费了。这时候需要我们使用循环数组。
循环数组怎么实现呢?只需要把数组的最后一个节点和数组的最前面的一个节点连接即可。
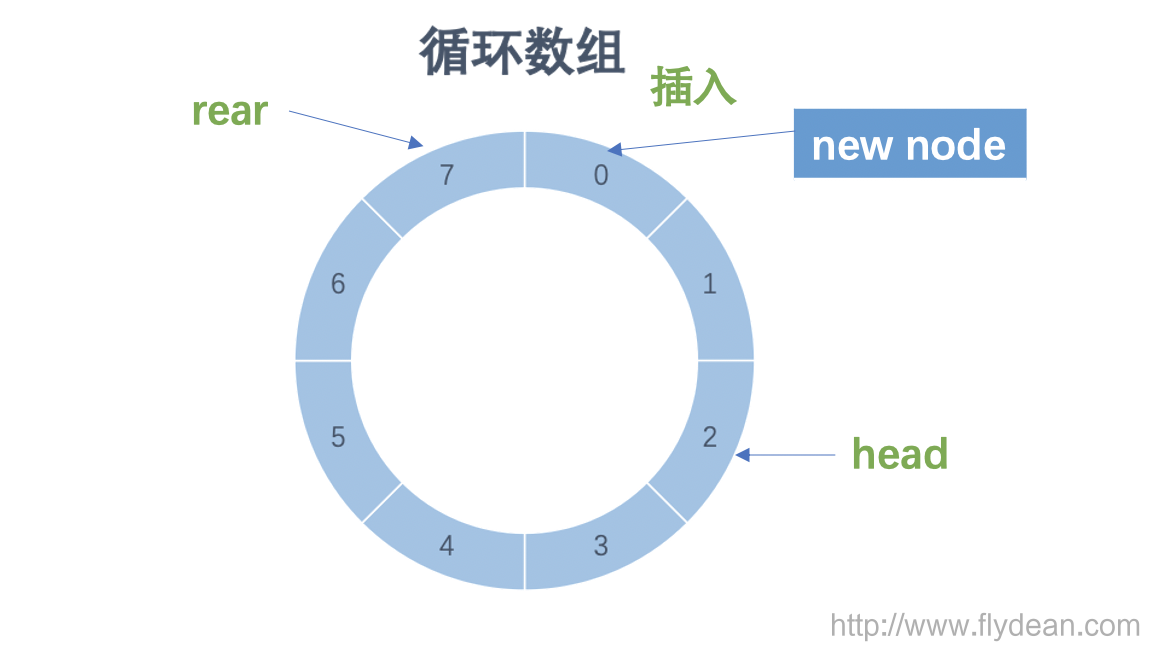
有同学又要问了。数组怎么变成循环数组呢?数组又不能像链表那样前后连接。
不急,我们先考虑一个余数的概念,假如我们知道了数组的capacity,当要想数组插入数据的时候,我们还是照常的将rear+1,但是最后除以数组的capacity, 队尾变到了队首,也就间接的实现了循环数组。
看下java代码是怎么实现的:
public class ArrayQueue {
//存储数据的数组
private int[] array;
//head索引
private int head;
//real索引
private int rear;
//数组容量
private int capacity;
public ArrayQueue (int capacity){
this.capacity=capacity;
this.head=-1;
this.rear =-1;
this.array= new int[capacity];
}
public boolean isEmpty(){
return head == -1;
}
public boolean isFull(){
return (rear +1)%capacity==head;
}
public int getQueueSize(){
if(head == -1){
return 0;
}
return (rear +1-head+capacity)%capacity;
}
//从尾部入队列
public void enQueue(int data){
if(isFull()){
System.out.println("Queue is full");
}else{
//从尾部插入
rear = (rear +1)%capacity;
array[rear]= data;
//如果插入之前队列为空,将head指向real
if(head == -1 ){
head = rear;
}
}
}
//从头部取数据
public int deQueue(){
int data;
if(isEmpty()){
System.out.println("Queue is empty");
return -1;
}else{
data= array[head];
//如果只有一个元素,则重置head和real
if(head == rear){
head= -1;
rear = -1;
}else{
head = (head+1)%capacity;
}
return data;
}
}
}
大家注意我们的enQueue和deQueue中使用的方法:
rear = (rear +1)%capacity
head = (head+1)%capacity
这两个就是循环数组的实现。
队列的动态数组实现
上面的实现其实有一个问题,数组的大小是写死的,不能够动态扩容。我们再实现一个能够动态扩容的动态数组实现。
//因为是循环数组,这里不能做简单的数组拷贝
private void extendQueue(){
int newCapacity= capacity*2;
int[] newArray= new int[newCapacity];
//先全部拷贝
System.arraycopy(array,0,newArray,0,array.length);
//如果real<head,表示已经进行循环了,需要将0-head之间的数据置空,并将数据拷贝到新数组的相应位置
if(rear< head){
for(int i=0; i< head; i++){
//重置0-head的数据
newArray[i]= -1;
//拷贝到新的位置
newArray[i+capacity]=array[i];
}
//重置real的位置
rear= rear+capacity;
//重置capacity和array
capacity=newCapacity;
array=newArray;
}
}
需要注意的是,在进行数组扩展的时候,我们不能简单的进行拷贝,因为是循环数组,可能出现rear在head后面的情况。这个时候我们需要对数组进行特殊处理。
其他部分是和普通数组实现基本一样的。
队列的链表实现
除了使用数组,我们还可以使用链表来实现队列,只需要在头部删除和尾部添加即可。
看下java代码实现:
public class LinkedListQueue {
//head节点
private Node headNode;
//rear节点
private Node rearNode;
class Node {
int data;
Node next;
//Node的构造函数
Node(int d) {
data = d;
}
}
public boolean isEmpty(){
return headNode==null;
}
public void enQueue(int data){
Node newNode= new Node(data);
//将rearNode的next指向新插入的节点
if(rearNode !=null){
rearNode.next=newNode;
}
rearNode=newNode;
if(headNode == null){
headNode=newNode;
}
}
public int deQueue(){
int data;
if(isEmpty()){
System.out.println("Queue is empty");
return -1;
}else{
data=headNode.data;
headNode=headNode.next;
}
return data;
}
}
队列的时间复杂度
上面的3种实现的enQueue和deQueue方法,基本上都可以立马定位到要入队列或者出队列的位置,所以他们的时间复杂度是O(1)。
本文的代码地址:
本文已收录于 http://www.flydean.com/12-algorithm-queue/
最通俗的解读,最深刻的干货,最简洁的教程,众多你不知道的小技巧等你来发现!
欢迎关注我的公众号:「程序那些事」,懂技术,更懂你!




 浙公网安备 33010602011771号
浙公网安备 33010602011771号