NumPy之:ndarray中的函数
NumPy之:ndarray中的函数
简介
在NumPy中,多维数组除了基本的算数运算之外,还内置了一些非常有用的函数,可以加快我们的科学计算的速度。
简单函数
我们先看下比较常见的运算函数,在使用之前,我们先构造一个数组:
arr = np.arange(10)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
计算数组中元素的开方:
np.sqrt(arr)
array([0. , 1. , 1.4142, 1.7321, 2. , 2.2361, 2.4495, 2.6458,
2.8284, 3. ])
自然常数e为底的指数函数:
np.exp(arr)
array([ 1. , 2.7183, 7.3891, 20.0855, 54.5982, 148.4132,
403.4288, 1096.6332, 2980.958 , 8103.0839])
取两个数组的最大值,组成新的数组:
x = np.random.randn(8)
y = np.random.randn(8)
x,y
(array([-2.3594, -0.1995, -1.542 , -0.9707, -1.307 , 0.2863, 0.378 ,
-0.7539]),
array([ 0.3313, 1.3497, 0.0699, 0.2467, -0.0119, 1.0048, 1.3272,
-0.9193]))
np.maximum(x, y)
array([ 0.3313, 1.3497, 0.0699, 0.2467, -0.0119, 1.0048, 1.3272,
-0.7539])
返 回浮点数数组的小数和整数部分:
arr = np.random.randn(7) * 5
array([-7.7455, 0.1109, 3.7918, -3.3026, 4.3129, -0.0502, 0.25 ])
remainder, whole_part = np.modf(arr)
(array([-0.7455, 0.1109, 0.7918, -0.3026, 0.3129, -0.0502, 0.25 ]),
array([-7., 0., 3., -3., 4., -0., 0.]))
矢量化数组运算
如果要进行数组之间的运算,常用的方法就是进行循环遍历,但是这样的效率会比较低。所以Numpy提供了数组之间的数据处理的方法。
先来讲解一下 np.meshgrid 这个函数,这个函数是用来快速生成网格点坐标矩阵的。
先看一段坐标点的代码:
import numpy as np
import matplotlib.pyplot as plt
x = np.array([[0, 1, 2], [0, 1, 2]])
y = np.array([[0, 0, 0], [1, 1, 1]])
plt.plot(x, y,
color='green',
marker='.',
linestyle='')
plt.grid(True)
plt.show()
上面的X是一个二维数组,表示的是坐标点的X轴的位置。
Y也是一个二维数组,表示的是坐标点的Y轴的位置。
看下画出来的图像:
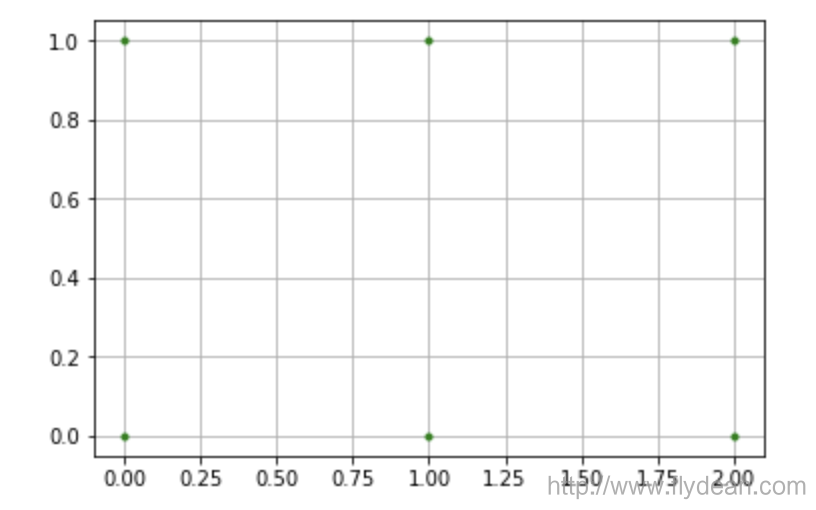
上面画出的就是使用X,Y矩阵组合出来的6个坐标点。
上面的X,Y的二维数组是我们手动输入的,如果坐标上面有大量点的话,手动输入肯定是不可取的。
于是有了np.meshgrid这个函数。这个函数可以接受两个一维的数组,然后生成二维的X,Y坐标矩阵。
上面的例子可以改写为:
x = np.array([0,1,2])
y = np.array([0,1])
xs, ys = np.meshgrid(x, y)
xs,ys
(array([[0, 1, 2],
[0, 1, 2]]),
array([[0, 0, 0],
[1, 1, 1]]))
可以看到生成的xs和ys和手动输入是一样的。
有了网格坐标之后,我们就可以基于网格值来计算一些数据,比如:\(sqrt(x^2+y^2)\) ,我们不用变量矩阵中所有的数据,只需要直接使用数组进行运算即可:
np.sqrt(xs ** 2 + ys ** 2)
结果:
array([[0. , 1. , 2. ],
[1. , 1.41421356, 2.23606798]])
因为xs 和ys本身就是2 * 3 的矩阵,所以结果也是 2 * 3 的矩阵。
条件逻辑表达式
我们可以在构建数组的时候使用条件逻辑表达式:
xarr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])
yarr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])
cond = np.array([True, False, True, True, False])
result = [(x if c else y)
for x, y, c in zip(xarr, yarr, cond)]
result
[1.1, 2.2, 1.3, 1.4, 2.5]
更简单一点,我们可以使用where语句:
result = np.where(cond, xarr, yarr)
result
array([1.1, 2.2, 1.3, 1.4, 2.5])
我们还可以根据where的条件来修改数组的值:
arr = np.random.randn(4, 4)
arr
array([[ 0.7953, 0.1181, -0.7485, 0.585 ],
[ 0.1527, -1.5657, -0.5625, -0.0327],
[-0.929 , -0.4826, -0.0363, 1.0954],
[ 0.9809, -0.5895, 1.5817, -0.5287]])
上面我们构建了一个4 * 4 的数组。
我们可以在where中进行数据的比较,如果大于0,将数据修改成2 ,如果小于0,则将数据修该成-2 :
np.where(arr > 0, 2, -2)
array([[ 2, 2, -2, 2],
[ 2, -2, -2, -2],
[-2, -2, -2, 2],
[ 2, -2, 2, -2]])
统计方法
numpy提供了mean,sum等统计方法:
arr = np.random.randn(5, 4)
arr
arr.mean()
np.mean(arr)
arr.sum()
还可以按维度来统计:
arr.mean(axis=1)
arr.sum(axis=0)
cumsum进行累加计算:
arr = np.array([0, 1, 2, 3, 4, 5, 6, 7])
arr.cumsum()
array([ 0, 1, 3, 6, 10, 15, 21, 28])
cumprod进行累乘计算:
arr = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
arr
arr.cumsum(axis=0)
array([[ 0, 1, 2],
[ 3, 5, 7],
[ 9, 12, 15]])
arr.cumprod(axis=1)
array([[ 0, 0, 0],
[ 3, 12, 60],
[ 6, 42, 336]])
布尔数组
any用于测试数组中是否存在一个或多个True,而all则检查数组中所有值是否都是True:
bools = np.array([False, False, True, False])
bools.any()
True
bools.all()
False
排序
使用sort可以对数组进行排序,除了普通排序还可以按照特定的轴来进行排序:
arr = np.random.randn(6)
arr.sort()
array([-2.5579, -1.2943, -0.2972, -0.1516, 0.0765, 0.1608])
arr = np.random.randn(5, 3)
arr
arr.sort(1)
arr
array([[-0.8852, -0.4936, -0.1875],
[-0.3507, -0.1154, 0.0447],
[-1.1512, -0.8978, 0.8909],
[-2.6123, -0.8671, 1.1413],
[-0.437 , 0.3475, 0.3836]])
sort(1)指的是按照第二个轴来排序。
文件
可以方便的将数组写入到文件和从文件中读出:
arr = np.arange(10)
np.save('some_array', arr)
会将数组存放到some_array.npy文件中,我们可以这样读取:
np.load('some_array.npy')
还可以以无压缩的方式存入多个数组:
np.savez('array_archive.npz', a=arr, b=arr)
读取:
arch = np.load('array_archive.npz')
arch['b']
如果想要压缩,可以这样:
np.savez_compressed('arrays_compressed.npz', a=arr, b=arr)
线性代数
如果我们使用普通的算数符来进行矩阵的运算的话,只是简单的数组中对应的元素的算数运算。如果我们想做矩阵之间的乘法的时候,可以使用dot。
一个 2 * 3 的矩阵 dot 一个3*2 的矩阵,最终得到一个2 * 2 的矩阵。
x = np.array([[1., 2., 3.], [4., 5., 6.]])
y = np.array([[6., 23.], [-1, 7], [8, 9]])
x
y
x.dot(y)
array([[ 28., 64.],
[ 67., 181.]])
或者可以这样写:
np.dot(x, y)
array([[ 28., 64.],
[ 67., 181.]])
还可以使用 @ 符号:
x @ y
array([[ 28., 64.],
[ 67., 181.]])
我们看下都有哪些运算:
乘积运算:
| 操作符 | 描述 |
|---|---|
| dot(a, b[, out]) | 矩阵点积 |
| linalg.multi_dot(arrays, *[, out]) | 多个矩阵点积 |
| vdot(a, b) | 向量点积 |
| inner(a, b) | 两个数组的内积 |
| outer(a, b[, out]) | 两个向量的外积 |
| matmul(x1, x2, /[, out, casting, order, …]) | 两个矩阵的对应位的乘积 |
| tensordot(a, b[, axes]) | 计算沿指定轴的张量点积 |
| einsum(subscripts, *operands[, out, dtype, …]) | 爱因斯坦求和约定 |
| einsum_path(subscripts, *operands[, optimize]) | 通过考虑中间数组的创建,评估einsum表达式的最低成本收缩顺序。 |
| linalg.matrix_power(a, n) | 矩阵的幂运算 |
| kron(a, b) | 矩阵的Kronecker乘积 |
分解运算:
| 操作符 | 描述 |
|---|---|
| linalg.cholesky(a) | Cholesky 分解 |
| linalg.qr(a[, mode]) | 计算矩阵的qr因式分解 |
| linalg.svd(a[, full_matrices, compute_uv, …]) | 奇异值分解 |
本征值和本征向量:
| 操作 | 描述 |
|---|---|
| linalg.eig(a) | 计算方阵的特征值和右特征向量。 |
| linalg.eigh(a[, UPLO]) | 返回复数Hermitian(共轭对称)或实对称矩阵的特征值和特征向量。 |
| linalg.eigvals(a) | 计算通用矩阵的特征值。 |
| linalg.eigvalsh(a[, UPLO]) | 计算复数Hermitian(共轭对称)或实对称矩阵的特征值。 |
基准值:
| 操作 | 描述 |
|---|---|
| linalg.norm(x[, ord, axis, keepdims]) | 矩阵或向量范数 |
| linalg.cond(x[, p]) | Compute the condition number of a matrix. |
| linalg.det(a) | 矩阵行列式 |
| linalg.matrix_rank(M[, tol, hermitian]) | 使用SVD方法返回数组的矩阵秩 |
| linalg.slogdet(a) | 计算数组行列式的符号和(自然)对数。 |
| trace(a[, offset, axis1, axis2, dtype, out]) | 返回沿数组对角线的和。 |
求解和反转:
| 操作 | 描述 |
|---|---|
| linalg.solve(a, b) | 求解线性矩阵方程或线性标量方程组。 |
| linalg.tensorsolve(a, b[, axes]) | 对x求解张量方程'a x = b'。 |
| linalg.lstsq(a, b[, rcond]) | 将最小二乘解返回线性矩阵方程 |
| linalg.inv(a) | 计算矩阵的(乘法)逆。 |
| linalg.pinv(a[, rcond, hermitian]) | 计算矩阵的(Moore-Penrose)伪逆。 |
| linalg.tensorinv(a[, ind]) | 计算N维数组的“逆”。 |
随机数
很多时候我们都需要生成随机数,在NumPy中随机数的生成非常简单:
samples = np.random.normal(size=(4, 4))
samples
array([[-2.0016, -0.3718, 1.669 , -0.4386],
[-0.5397, 0.477 , 3.2489, -1.0212],
[-0.5771, 0.1241, 0.3026, 0.5238],
[ 0.0009, 1.3438, -0.7135, -0.8312]])
上面用normal来得到一个标准正态分布的4×4样本数组。
使用np.random要比使用Python自带的随机数生成器要快得多。
np.random可以指定生成随机数的种子:
np.random.seed(1234)
numpy.random的数据生成函数使用了全局的随机种子。要避免 全局状态,你可以使用numpy.random.RandomState,创建一个 与其它隔离的随机数生成器:
rng = np.random.RandomState(1234)
rng.randn(10)
本文已收录于 http://www.flydean.com/10-python-numpy-func/
最通俗的解读,最深刻的干货,最简洁的教程,众多你不知道的小技巧等你来发现!
欢迎关注我的公众号:「程序那些事」,懂技术,更懂你!




 浙公网安备 33010602011771号
浙公网安备 33010602011771号