变化的电磁场
电磁感应定律
电磁感应现象:当穿过闭合回路的磁通量发生变化时,不管这种变化是由于什么原因引起的,回路中都有电流产生,这种现象称为电磁感应现象,回路中产生的电流称为感应电流
法拉第电磁感应定律
电磁感应定律定量表达式:导体回路中产生的感应电动势的大小,与穿过导体回路的磁通量对时间 的变化率成正比
\[\varepsilon_i=-\frac{dN\Phi_m}{dt}
\]
其中N为匝数
据此,穿过导线截面的感应电量为:
\[q=-\int_{t_1}^{t_2}\frac{1}{R}\frac{d\Phi_m}{dt}dt=\frac{1}{R}(\Phi_1-\Phi_2)
\]
楞次定律
楞次定律:闭合回路中感应电流的方向总是使其所激发的磁场来阻止或者补偿引起感应电流的磁通量变化
动生电动势和感生电动势
动生电动势:
动生电动势使由于导体或者导体回路在恒定磁场中运动而产生的电动势
动生电动势公式:
\[\varepsilon_i=\int_b^a(\vec v \times \vec B)\cdot d\vec l
\]
感生电动势和感生电场
感生电动势
由于磁场发生变化而激发的电动势
麦克斯韦假设:
变化的磁场在其周围空间会激发一种涡旋状的电场,称为涡旋电场或感生电场
\[\oint_L \vec E_涡\cdot\vec l=-\int_s\frac{\partial\vec B}{\partial\vec t}\cdot d\vec S
\]
自感与互感
自感现象
回路自身电流、回路的形状、或回路周围的磁介质发生变化时,穿过该回路自身的磁通量随之变化,从而在回路中产生感应电动势的现象
\[\psi=LI
\]
其中L为自感系数\(\psi=N\phi_m\),单位为亨利,则自感电动势为:
\[\varepsilon_L=-\frac{d(LI)}{dt}=-L\frac{dI}{dt}-I\frac{dL}{dt}
\]
若只有电流大小发生了改变,则$$\varepsilon_L=-L\frac{dI}{dt}$$
L总是阻碍电流的变化
互感现象
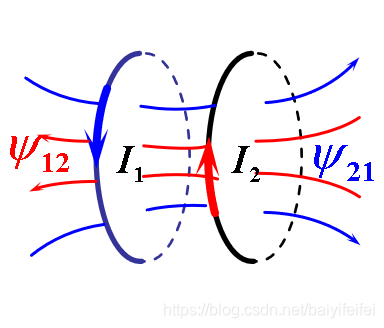
因两个载流线圈中电流变化而在对方线圈中激起感应电动势的现象称为互感应现象
![在这里插入图片描述]()
\[\Psi_{21}=M_{21}I_1,\Psi_{12}=M_{12}I_2
\]
其中M为互感系数,据实验\(M_{21}=M_{12}\)
\[\varepsilon_{12}=-\frac{d\Psi_{12}}{dt}=-M\frac{dI_2}{dt},\varepsilon_{21}=-\frac{d\Psi_{21}}{dt}=-M\frac{dI_1}{dt}
\]
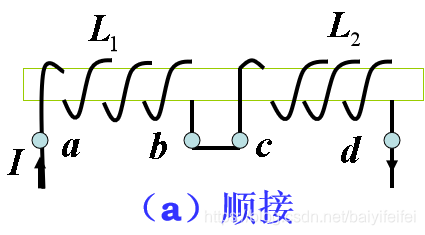
自感线圈的串联
![在这里插入图片描述]()
等效电感为:
\[L=L_1+L_2+2M
\]
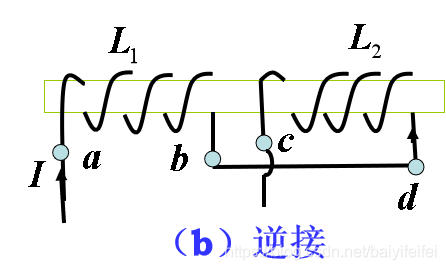
![在这里插入图片描述]()
\[L=L_1+L_2-2M
\]
- 为了反应两个回路磁场耦合的松紧程度,引入了耦合系数的概念
\[M=k\sqrt{L_1L_2}
\]
其中k即为耦合系数
在一般情况下,由于漏磁等现象,k<1
磁场能量
自感能量
在一仅有电阻与电感的电路中,电流的随时间变化有如下公式$$i=\frac{\varepsilon}{R}(1-e^{-\frac{R}{L}t})$$
在完成充电之后,电感拥有能量
\[W=\frac{1}{2}LI^2
\]
互感能量
两个相邻的线圈分别与电源相连,在通电过程中,两线圈的磁能为:
\[W=\frac{1}{2}L_1I_1^2+\frac{1}{2}L_2I_2^2+MI_1I_2
\]
磁场的能量
由螺线管特例\(W=\frac{1}{2}BHV\)可以推出
\[W=\int_vwdV=\int_v\frac{1}{2}BHdV
\]
麦克斯韦电磁场理论
电容器上极板在充放电过程中,造成极板上电荷累积随时间变化,单位时间内极板上电荷的增加或减少等于通入或流入极板的电流
\[I=\frac{dQ}{dt}=\int_s\frac{\partial\vec D}{\partial t}\cdot d\vec S
\]
此即是位移电流,其电流密度为
\[\vec j_d=\frac{\partial\vec D}{\partial t}
\]
全电流定律
全电流定律:通过某一截面的全电流是通过这一截面的传导电流、运流电流和位移电流的代数和
麦克斯韦方程
\[\begin{cases}\oint_s\vec D\cdot d\vec S=\sum q&说明静电场是有源场\\\oint_L\vec E\cdot d\vec l=0&说明静电场是保守场、无旋场\\\oint_s \vec B\cdot d\vec S=0&稳恒磁场是无源场
\\\oint_L\vec H\cdot d\vec l=\sum I&稳恒磁场是非保守场\end{cases}\]
自由空间的麦克斯韦方程
\[\begin{cases}\oint_s\vec D\cdot d\vec S=0\\\oint_L\vec E \cdot d\vec l=-\int_s\frac{\partial\vec B}{\partial t}\cdot d\vec S\\\oint_s\vec B\cdot d \vec S=0\\\oint_L\vec H\cdot d\vec l=\int_s\frac{\partial\vec D}{\partial t}d\vec S\end{cases}
\]
介质的物质方程
\[\vec D=\varepsilon\vec E
\]
\[\vec B=\mu E
\]
\[\vec j=\sigma\vec E
\]
其中\(\sigma\)为电导率
电磁波
据麦克斯韦理论:
\[\oint_L\vec E \cdot d\vec l=-\int_s\frac{\partial\vec B}{\partial t}\cdot d\vec S,\oint_L\vec H\cdot d\vec l=\int_s\frac{\partial\vec D}{\partial t}d\vec S
\]
这样,电场与磁场可以互相激发,以波的形式在空间中传播
电磁波的性质
- 电磁波是横波,电场强度,磁场强度,电磁波速度相互垂直,构成正交右旋,
- 电磁波是偏振波
- 电场强度与磁场强度同相位
- 同一点的电场强度与磁场强度满足\(\sqrt\varepsilon E=\sqrt\mu H\)
- 传播速度为\(v=\frac{1}{\sqrt{\varepsilon\mu}}\)近似光速
电磁波的能量
能量密度
据\(w_e=\frac{1}{2}\varepsilon E^2,w_m=\frac{1}{2}\mu H^2\)得到电磁场的能量密度为$$w=\varepsilon E^2=\mu E^2$$
能流密度
单位时间内穿过垂直于传播方向的单位面积的辐射能量(s)
\[\vec S=\vec E \times \vec H
\]
电磁波的辐射
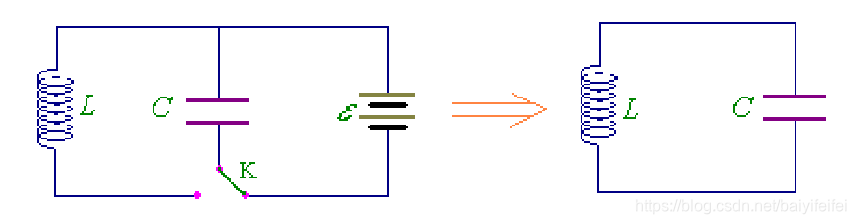
电磁振荡
![在这里插入图片描述]()
一个不计电阻的LC电路可以实现电磁振荡,且有频率
\[\omega=\frac{1}{\sqrt{LC}}
\]
缺点
(1)振荡频率低
(2)电磁场仅局限于电容器与自感线圈之间


 浙公网安备 33010602011771号
浙公网安备 33010602011771号