二分法求最小值的最大值，最大值的最小值的问题
最近刚遇上了这类问题，起初苦想没有思路，在网上学习了别人的解法之后感觉到精妙异常，虽然事后知道只是一个模板题，但还是想要总结一下。
先举个例子是POJ的3273题 http://poj.org/problem?id=327
Description
Farmer John is an astounding accounting wizard and has realized he might run out of money to run the farm. He has already calculated and recorded the exact amount of money (1 ≤moneyi ≤ 10,000) that he will need to spend each day over the nextN (1 ≤ N ≤ 100,000) days.
FJ wants to create a budget for a sequential set of exactly M (1 ≤M ≤N) fiscal periods called "fajomonths". Each of these fajomonths contains a set of 1 or more consecutive days. Every day is contained in exactly one fajomonth.
FJ's goal is to arrange the fajomonths so as to minimize the expenses of the fajomonth with the highest spending and thus determine his monthly spending limit.
Input
Line 1: Two space-separated integers:
N andM
Lines 2..N+1: Line i+1 contains the number of dollars Farmer John spends on theith day
Lines 2..N+1: Line i+1 contains the number of dollars Farmer John spends on theith day
Output
Line 1: The smallest possible monthly limit Farmer John can afford to live with.
Sample Input
7 5 100 400 300 100 500 101 400
Sample Output
500
Hint
If Farmer John schedules the months so that the first two days are a month, the third and fourth are a month, and the last three are their own months, he spends at most $500 in any month. Any other method of scheduling
gives a larger minimum monthly limit.
题目大意是共计N天，并已知每天的花费，要求把这N天分成连续的m组，在求得各组花费之和后，取出其中的最大值，问如何使这个最大值（令为X）尽量小。
本题的思路是假设M=N时取得一个最大值Xlift（即N天中花费最多的那天）和M=1时取得一个最大值xright（即所有天的花费之和）。而我们所要求的M=m时的最大值的最小值就在这条“最大值路径上”而只要通过不断地取最大值Xmid与这时的分段数和m比较，来不断逼近题目所给的m就最终能求出我们所要的答案。
这是我看到的网上的大多数帖子的思路，一开始百思不得其解，这样不是只能求出分段m时的最大值的区间吗？这样所求出的只能说是分段数为m时可能的最大值而不能说是最大值的最小值啊。一时间被搞得晕头转向的。好在有学长的提点，并最终发现了题目的真相：
这个逼近的过程做了两件事情：
1.通过不断的逼近来确定分段数为m时的最大值的区间
2.通过逼近来找到这个区间的左边界
#include<stdio.h>
int money[100005];
int main()
{
int n,m,i,small=-1,big=0,u,sum=0,mid;
scanf("%d%d",&n,&m);
for(i=0;i<n;i++)
{
scanf("%d",&money[i]);
if(small<money[i]) small=money[i];
big+=money[i];
}
while(small<big)
{
mid=(big+small)/2;u=1;sum=0;
for(i=0;i<n;i++)
{
if(sum+money[i]>mid)
{
u++;
sum=money[i];
}
else sum+=money[i];
}
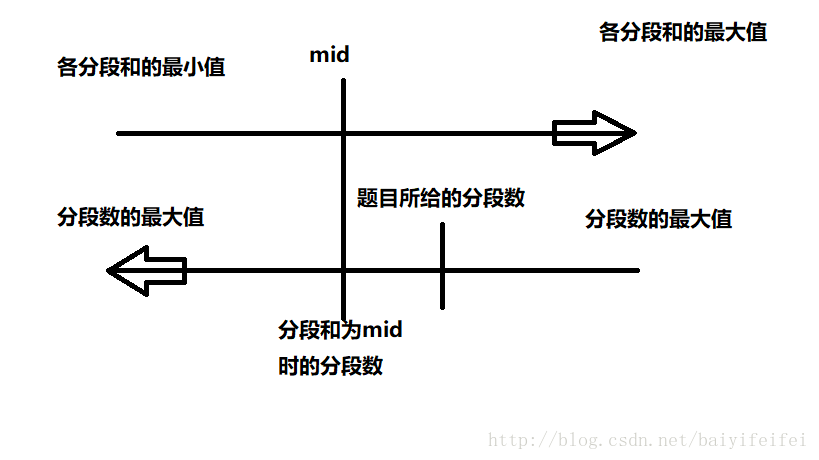
if(u<=m)//这个小于等于的小于部分用于都一阶段也就是求出最大值区间，等于号来求这个区间的左边界
big=mid;
else
small=mid+1;
}
printf("%d\n",big);
} 这道题只要还是借鉴了网上的模板，当时刚仿写的时候对题目的本质还没有了解，并不大懂，有做了下面这一题才好一些。
这题和上一题大同小异，不过求的是最小值的最大值
POJ2456题，链接：http://poj.org/problem?id=2456
Aggressive cows
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 17346 | Accepted: 8256 |
Description
Farmer John has built a new long barn, with N (2 <= N <= 100,000) stalls. The stalls are located along a straight line at positions x1,...,xN (0 <= xi <= 1,000,000,000).
His C (2 <= C <= N) cows don't like this barn layout and become aggressive towards each other once put into a stall. To prevent the cows from hurting each other, FJ want to assign the cows to the stalls, such that the minimum distance between any two of them is as large as possible. What is the largest minimum distance?
His C (2 <= C <= N) cows don't like this barn layout and become aggressive towards each other once put into a stall. To prevent the cows from hurting each other, FJ want to assign the cows to the stalls, such that the minimum distance between any two of them is as large as possible. What is the largest minimum distance?
Input
* Line 1: Two space-separated integers: N and C
* Lines 2..N+1: Line i+1 contains an integer stall location, xi
* Lines 2..N+1: Line i+1 contains an integer stall location, xi
Output
* Line 1: One integer: the largest minimum distance
Sample Input
5 3 1 2 8 4 9
Sample Output
3
Hint
OUTPUT DETAILS:
FJ can put his 3 cows in the stalls at positions 1, 4 and 8, resulting in a minimum distance of 3.
Huge input data,scanf is recommended.
FJ can put his 3 cows in the stalls at positions 1, 4 and 8, resulting in a minimum distance of 3.
Huge input data,scanf is recommended.
Source
和上一题一样的原理，不过因为求的是最大值所以选择从左向右逼近
#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
int x[100005];
int main()
{
int n,m,i,small=-1,big=0,right,left,mid,cnt,sum,num,l,r,p,u;
scanf("%d%d",&n,&m);
for(i=0;i<n;i++)
{
scanf("%d",&x[i]);
small=min(small,x[i]);
}
sort(x,x+n);
big=x[n-1]-x[0];
num=x[n-1]/(m-1);
left=0;right=num;
while(right-left>1)
{
mid=(left+right)/2;
l=1;r=1;p=1;
while(r<n){
while(r<=n&&x[l-1]+mid>x[r-1]) r++;
if(r>n) break;
p++;l=r;if(p==m)break;
}
if(p==m) left=mid;
else right=mid;
}
printf("%d\n",left);
}一样的思路，不过这题的写法更加规整一点，真正把求得区间和取得，思路更加清晰了，最小值的最大值分开算了。需要注意的是因为是乱序输入x[i]所以要注意排序。这题依旧是借鉴居多自己的思考偏少，下一题才真正是我完全理解了之后做出来的。
POJ3122题，链接：http://poj.org/problem?id=3122
Pie
| Time Limit: 1000MS | Memory Limit: 65536K | |||
| Total Submissions: 19777 | Accepted: 6420 | Special Judge | ||
Description
My birthday is coming up and traditionally I'm serving pie. Not just one pie, no, I have a number N of them, of various tastes
and of various sizes. F of my friends are coming to my party and each of them gets a piece of pie. This should be one piece of one pie, not several small pieces since that looks messy. This piece can be one whole pie though.My friends are very annoying and if one of them gets a bigger piece than the others, they start complaining. Therefore all of them should get equally sized (but not necessarily equally shaped) pieces, even if this leads to some pie getting spoiled (which is better than spoiling the party). Of course, I want a piece of pie for myself too, and that piece should also be of the same size.
What is the largest possible piece size all of us can get? All the pies are cylindrical in shape and they all have the same height 1, but the radii of the pies can be different.
Input
One line with a positive integer: the number of test cases. Then for each test case:
- One line with two integers N and F with 1 ≤ N, F ≤ 10 000: the number of pies and the number of friends.
- One line with N integers ri with 1 ≤ ri ≤ 10 000: the radii of the pies.
Output
For each test case, output one line with the largest possible volume V such that me and my friends can all get a pie piece of size V. The answer should be given as a floating point number with an absolute error of
at most 10−3.
Sample Input
3 3 3 4 3 3 1 24 5 10 5 1 4 2 3 4 5 6 5 4 2
Sample Output
25.1327 3.1416 50.2655
Source
思路还是一样，就不赘述了。需要注意的是这题的数据是浮点型的，所以left不可能大于等于right了，所以要选择一个精度，当左右值的差距小于精度的时候就可以退出循环了。同样值得一提的是因为一些编译器的原因，下面的代码是用c++交的，而不是通常的g++否则会WA，当然据说也可以通过把最后的输出改成printf("%.4f\n",big*acos(-1.0));来AC不过我也没有试过就不再妄谈了，倒是正好找到了一篇如何选择C++与G++的博客，很巧的是正好讲的这道题目，链接在下面有兴趣的朋友可以看。
链接：http://blog.csdn.net/liuke19950717/article/details/48421855
#include<stdio.h>
#include<math.h>
double pi[10005];
double lostpi[10005];
double area(double r)
{
return acos(-1.0)*r*r;
}
int main()
{
int n,f,much,i,sum;
double mid,big,small;
int t;
scanf("%d",&t);
while(t--)
{
small=0;big=0;
scanf("%d%d",&n,&f);
for(i=0;i<n;i++)
{
scanf("%lf",&pi[i]);
//pi[i]=area(pi[i]);
pi[i]=pi[i]*pi[i];
lostpi[i]=pi[i];
if(pi[i]>big)big=pi[i];
//printf("%lf\n",lostpi[i]);
}
while(0.000001<=big-small)
{
much=0;mid=(big+small)/2;
//printf("%lf\n",big);
for(i=0;i<n;i++)
{
lostpi[i]=pi[i];
while(lostpi[i]>=mid)
{
much++;
lostpi[i]-=mid;
//printf("PI%lf\n",lostpi[i]);printf("%d\n",much);
}
}
if(much>=f+1) small=mid;
else big=mid;
//printf("small%lfbig%lf\n",small,big);
//if(--u) continue;
//else break;
}
printf("%.4lf\n",big*acos(-1.0));
}
} 好了大概是就是这几个题目了，来找出最大值的最小值或者最小值的最大值，有整型的有浮点型的，只要注意好可以通过逼近来退出循环就可以了。至于逼近方向的选择和最x值的最y值中的x无关而只与y有关。
用图解做一个总结
对应图解理解第一阶段，第一条直线是通过取分段数的和的最值的最大情况和最小情况构造出来的路径，我们所有求的最值必然在这条路径上，但第一步还是先缩小范围，找出分题目所给段数时的最值区间，具体操作就是当mid对应的分段数比题目所给小时就使left=mid;以取得左边的分段来靠近题目所给的分段数，反之则right=mid;同样解释。图示并不足够准确因为每一个分段数对应的是一个区间而非一个点，但考虑到电脑自带的画图功能实在不好画就只能画到这种地步了。
这是第二阶段的图解。因为虽然通过第一阶段已经找出分段数为题目所给的数（设为M)时的最X值区间，但循环并未结束，若向右逼近则不断使left=mid；直到left和right的距离达到想要的精度为止；反之若向左逼近则同理让right=mid;即可
综上
if(mid对应的分段数<m) big=mid；
if(mid对应的分段数>m）left=mid(+1);
if(mid对应的分段数==m) 若求最x值的最大值left=mid:若求最x值的最小值right=mid
一遍理下来思路我的更加清晰了，也希望对看到的你有所帮助。
