暑假训练DAY4(递推&递归)
一只小蜜蜂...
http://acm.hdu.edu.cn/showproblem.php?pid=2044
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 93324 Accepted Submission(s): 33220
Problem Description
有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房,不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。
其中,蜂房的结构如下所示。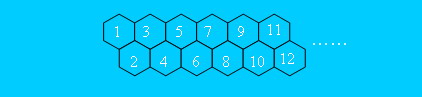
Input
输入数据的第一行是一个整数N,表示测试实例的个数,然后是N 行数据,每行包含两个整数a和b(0<a<b<50)。
Output
对于每个测试实例,请输出蜜蜂从蜂房a爬到蜂房b的可能路线数,每个实例的输出占一行。
Sample Input
2 1 2 3 6
Sample Output
1 3
Author
lcy
Source
a[n]=a[n-1]+a[n-2]
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
LL a[100];
int main()
{
a[0]=0;
a[1]=1;
a[2]=2;
for(int i=3;i<50;i++)
{
a[i]=a[i-1]+a[i-2];
}
int t;
cin>>t;
while(t--)
{
int x,y;
cin>>x>>y;
cout<<a[y-x]<<endl;
}
return 0;
}折线分割平面
http://acm.hdu.edu.cn/showproblem.php?pid=2050
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 37737 Accepted Submission(s): 25261
Problem Description
我们看到过很多直线分割平面的题目,今天的这个题目稍微有些变化,我们要求的是n条折线分割平面的最大数目。比如,一条折线可以将平面分成两部分,两条折线最多可以将平面分成7部分,具体如下所示。
Input
输入数据的第一行是一个整数C,表示测试实例的个数,然后是C 行数据,每行包含一个整数n(0<n<=10000),表示折线的数量。
Output
对于每个测试实例,请输出平面的最大分割数,每个实例的输出占一行。
Sample Input
2 1 2
Sample Output
2 7
Author
lcy
Source
2059: Water Problem
http://acm.csu.edu.cn/csuoj/problemset/problem?pid=2059
Time Limit: 1 Sec Memory Limit: 128 Mb Submitted: 572 Solved: 196
Description
一条‘Z’形线可以将平面分为两个区域,那么由N条Z形线所定义的区域的最大个数是多少呢?每条Z形线由两条平行的无限半直线和一条直线段组成
Input
首先输入一个数字T(T<100),代表有T次询问 每次询问输入一个数字N(N<1e8),代表有N条Z形线
Output
对于每次询问,在一行输出N条‘Z’形线所能划分的区域的最大个数为多少
Sample Input
2
1
2Sample Output
2
12
Hint

这两题在我的另一篇博客里都有详细的推导,并对这一类问题进行了总结,指路:https://blog.csdn.net/baiyifeifei/article/details/81218404
这里就贴一下代码:
V型线
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
LL a[10005];
int main()
{
int t;
cin>>t;
a[1]=2;a[2]=7;
for(LL i=3;i<=10000;i++)
{
a[i]=a[i-1]+4*i-3;
}
while(t--)
{
long long x;
cin>>x;
long long ans=a[x];
cout<<ans<<endl;
}
return 0;
}
z型线
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
int main()
{
int t;
cin>>t;
while(t--)
{
LL x;
cin>>x;
cout<<3*x*(x*3+1)/2+1-5*x<<endl;
}
return 0;
}放苹果
http://poj.org/problem?id=1664
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 37060 | Accepted: 22820 |
Description
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?(用K表示)5,1,1和1,5,1 是同一种分法。
Input
第一行是测试数据的数目t(0 <= t <= 20)。以下每行均包含二个整数M和N,以空格分开。1<=M,N<=10。
Output
对输入的每组数据M和N,用一行输出相应的K。
Sample Input
1
7 3
Sample Output
8对于i个苹果向j个盘子中装的情况,可以视作至少一个盘子没装,和所有盘子均装满的的情况
而在分析所有盘子装满的情况时,先将i个苹果中取出j个给每个盘子都放上一个,则这种情况就失去全部装满的限制。
当盘子数多于i时则只有i个盘子生效则此时j就作为i处理
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
int a[25][25];
using namespace std;
int main()
{
int i,j;
for(i=0;i<=20;i++) a[i][1]=1;
for(j=0;j<=20;j++) a[0][j]=1;
for(i=0;i<=20;i++)
{
for(j=1;j<=20;j++)
{
if(i>=j)
a[i][j]=a[i][j-1]+a[i-j][j];
else a[i][j]=a[i][i-1]+a[0][j];
}
}
int t;
cin>>t;
while(t--)
{
int m,n;
cin>>m>>n;
cout<<a[m][n]<<endl;
}
return 0;
}母牛的故事
http://acm.hdu.edu.cn/showproblem.php?pid=2018
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 104956 Accepted Submission(s): 51490
Problem Description
有一头母牛,它每年年初生一头小母牛。每头小母牛从第四个年头开始,每年年初也生一头小母牛。请编程实现在第n年的时候,共有多少头母牛?
Input
输入数据由多个测试实例组成,每个测试实例占一行,包括一个整数n(0<n<55),n的含义如题目中描述。
n=0表示输入数据的结束,不做处理。
Output
对于每个测试实例,输出在第n年的时候母牛的数量。
每个输出占一行。
Sample Input
2 4 5 0
Sample Output
2 4 6
Author
lcy
Source
a[i]=a[i-3]+a[i-1]
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
LL a[60];
int main()
{
a[1]=1;a[2]=2;a[3]=3;a[4]=4;
for(int i=5;i<=55;i++)
{
a[i]=a[i-3]+a[i-1];
}
int n;
while(cin>>n&&n)
{
cout<<a[n]<<endl;
}
return 0;
}汉诺塔II
http://acm.hdu.edu.cn/showproblem.php?pid=1207
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 10044 Accepted Submission(s): 4903
Problem Description
经典的汉诺塔问题经常作为一个递归的经典例题存在。可能有人并不知道汉诺塔问题的典故。汉诺塔来源于印度传说的一个故事,上帝创造世界时作了三根金刚石柱子,在一根柱子上从下往上按大小顺序摞着64片黄金圆盘。上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一回只能移动一个圆盘。有预言说,这件事完成时宇宙会在一瞬间闪电式毁灭。也有人相信婆罗门至今仍在一刻不停地搬动着圆盘。恩,当然这个传说并不可信,如今汉诺塔更多的是作为一个玩具存在。Gardon就收到了一个汉诺塔玩具作为生日礼物。
Gardon是个怕麻烦的人(恩,就是爱偷懒的人),很显然将64个圆盘逐一搬动直到所有的盘子都到达第三个柱子上很困难,所以Gardon决定作个小弊,他又找来了一根一模一样的柱子,通过这个柱子来更快的把所有的盘子移到第三个柱子上。下面的问题就是:当Gardon在一次游戏中使用了N个盘子时,他需要多少次移动才能把他们都移到第三个柱子上?很显然,在没有第四个柱子时,问题的解是2^N-1,但现在有了这个柱子的帮助,又该是多少呢?
Input
包含多组数据,每个数据一行,是盘子的数目N(1<=N<=64)。
Output
对于每组数据,输出一个数,到达目标需要的最少的移动数。
Sample Input
1 3 12
Sample Output
1 5 81
Author
Gardon
Source
考虑到有四根柱子,设F[n]为所求的最小步数,我们将n个盘从第三根柱子移动到第一根柱子分成以下几步:
(1)将x(1<=x<=n)个盘从a柱依靠b,d柱移到c柱,这个过程需要的步数为F[x];
(2)将a柱上剩下的n-x个盘依靠b柱移到d柱(注:此时不能够依靠c柱,因为c柱上的所有盘都比a柱上的盘小)这时移动方式相当于是一个经典汉诺塔,即这个过程需要的步数为2^(n-x)-1
(3)将c柱上的x个盘依靠a,b柱移到d柱上,这个过程需要的步数为F[x];
再对x从1到n遍历出最小值即为F[n]
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
unsigned long long ans[65];
inline unsigned long long po(int j)
{
unsigned long long a=1;
for(int i=1;i<=j;i++)
a*=2;
return a;
}
void init()
{
ans[1]=1;
ans[2]=3;
for(long long i=3;i<=64;i++)
{
ans[i]=2*ans[i-1]+1;
for(long long j=2;j<i;j++)
{
ans[i]=min(ans[i],2*ans[i-j]+po(j)-1);
}
}
}
int main()
{
init();
int n;
while(cin>>n)
{
cout<<ans[n]<<endl;
}
return 0;
}1587: 爬楼梯
http://acm.csu.edu.cn/csuoj/problemset/problem?pid=1587
Submit Page Summary Time Limit: 1 Sec Memory Limit: 128 Mb Submitted: 863 Solved: 510
Description
小时候我们都玩过爬楼梯的游戏:两人猜拳,赢了可向上爬一级,谁先到最高级则获胜。作为大学生,我们应该玩一个更有水平的游戏。
现在一个人要上n级楼梯,每一步可以选择上一级或者上两级,但是不能后退。求上这n级楼梯的方案数。
Input
第一行只有一个整数T(1<=T<=45),表示数据组数。
下面的T行每一行有一个整数n(1<=n<=45),表示有多少级楼梯。
Output
对于每一组数据输出一个整数s,表示方案数。
Sample Input
4
1
2
3
4Sample Output
1
2
3
5Hint
Source
国防科学技术大学第十八届银河之光文化节ACM程序设计竞赛初赛
a[i]=a[i-1]+a[i-2];
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
LL a[50];
int main()
{
a[1]=1;a[2]=2;
for(int i=3;i<50;i++)
{
a[i]=a[i-1]+a[i-2];
}
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
cout<<a[n]<<endl;
}
return 0;
}神、上帝以及老天爷
http://acm.hdu.edu.cn/showproblem.php?pid=2048
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 50341 Accepted Submission(s): 20341
Problem Description
HDU 2006'10 ACM contest的颁奖晚会隆重开始了!
为了活跃气氛,组织者举行了一个别开生面、奖品丰厚的抽奖活动,这个活动的具体要求是这样的:
首先,所有参加晚会的人员都将一张写有自己名字的字条放入抽奖箱中;
然后,待所有字条加入完毕,每人从箱中取一个字条;
最后,如果取得的字条上写的就是自己的名字,那么“恭喜你,中奖了!”
大家可以想象一下当时的气氛之热烈,毕竟中奖者的奖品是大家梦寐以求的Twins签名照呀!不过,正如所有试图设计的喜剧往往以悲剧结尾,这次抽奖活动最后竟然没有一个人中奖!
我的神、上帝以及老天爷呀,怎么会这样呢?
不过,先不要激动,现在问题来了,你能计算一下发生这种情况的概率吗?
不会算?难道你也想以悲剧结尾?!
Input
输入数据的第一行是一个整数C,表示测试实例的个数,然后是C 行数据,每行包含一个整数n(1<n<=20),表示参加抽奖的人数。
Output
对于每个测试实例,请输出发生这种情况的百分比,每个实例的输出占一行, 结果保留两位小数(四舍五入),具体格式请参照sample output。
Sample Input
1 2
Sample Output
50.00%
先设有n-1个人他们都没有抽中自己该抽中的签子,此时又来了第n个人,则第n个人本来可以抽中自己的签子但是他和n-1个人中的某一个中交换了签子,这样他们就都抽不到自己该抽中的签子了。又有n-1个人中有一个人抽中了他该抽的签子,但是他和一样抽中了自己该抽的签子的第n个人交换了签子,所以也是n个人都没抽中。
考虑到可能与第n个人交换的人有n-1个则在ans(n)为有n人没抽中自己该抽签子的情况数的假设下有下式:
ans[i]=(i-1)*(ans[i-2]+ans[i-1]);
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
double ans[25];
int main()
{
ans[0]=1;
ans[1]=0;
double tot=1;
for(int i=2;i<=20;i++)
{
ans[i]=(i-1)*(ans[i-2]+ans[i-1]);
}
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
tot=1;
for(double i=2;i<=n;i++)
tot*=i;
//cout<<ans[n]<<endl;
printf("%.2lf%%\n",ans[n]/tot*100);
}
return 0;
}





