暑假训练DAY5(深度优先搜索dfs)
#1049 : 后序遍历
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
在参与过了美食节之后,小Hi和小Ho在别的地方又玩耍了一阵子,在这个过程中,小Ho得到了一个非常有意思的玩具——一棵由小球和木棍连接起来的二叉树!
小Ho对这棵二叉树爱不释手,于是给它的每一个节点都标记了一个标号——一个属于A..Z的大写字母,并且没有任意两个节点的标号是一样的。小Hi也瞅准了这个机会,重新巩固了一下小Ho关于二叉树遍历的基础知识~就这样,日子安稳的过了两天。
这天,小Ho正好在求解这棵二叉树的前序、中序和后序遍历的结果,但是却在求出前序遍历和中序遍历之后不小心把二叉树摔到了地上,小球和木棍等零件散落了一地!
小Ho损失了心爱的玩具,正要嚎啕大哭起来,所幸被小Hi发现了,劝说道:“别着急,这不是零件都还在么?拼起来不就是了?”
“可是我忘记了二叉树长什么样子了!”小Ho沮丧道。
“这个简单,你不是刚刚求出了这棵二叉树的前序和中序遍历的结果么,利用这两个信息就可以还原出整棵二叉树来哦!”
“这样么?!!”小Ho止住了泪水,问道:“那要怎么做呢?”
没错!小Ho在这一周遇到的问题便是:给出一棵二叉树的前序和中序遍历的结果,还原这棵二叉树并输出其后序遍历的结果。
“这可就要从头说起了,我们先找一棵二叉树作为例子吧!”小Hi在纸上画了画,递给了小Ho。
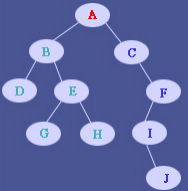
“不妨假设你的二叉树长成这个样子~”小Hi道。
“可是我的二叉树并不是长成这个样子啊!虽然我读书少,但是你不要骗我好不好!”小Ho一脸气愤道。
“我都说了是假设!是为了能让你明白如何通用的去解决这样的问题!”小Hi无奈道。
“好吧……你接着说。”小Ho算是认可了这个说法。
“那么对于这棵二叉树,你先来计算一下它的前序遍历和中序遍历的结果吧!”小Hi也是毫不含糊就开始下发任务。
“唔……前序遍历是ABDEGHCFIJ,中序遍历……我想想啊……是DBGEHACIJF!”小Ho并没有花费多长时间就给出了答案。
“你还记得前序遍历的递归定义么?”小Hi点了点头又继续问道。
“是‘根节点’+‘左子树的前序遍历’+‘右子树的前序遍历’!”小Ho毫不犹豫的答道:“而在这里体现出来就是‘A'+‘BDEGH’+‘CFIJ’”。
“那中序遍历呢?”小Hi继续问道。
“是‘左子树的中序遍历’+‘根节点’+‘右子树的中序遍历’!在这里也就是‘DBGEH’+‘A’+‘CIJF’。”小Ho这次花的时间更少了。
“还记得动态规划时候我们一般处理的方法么?我们这里也可以这样做哦,如果我们定义post_order(str1, str2)为一棵前序遍历的结果为str1,中序遍历的结果为str2的二叉树的后序遍历的结果的话,我们有没有办法把它化解成为子问题呢?”小Hi道。
“让我想想……”小Ho拿出纸笔开始演算起来:“如果我要求解post-order(str1, str2)的话,首先不难发现,根据‘前序遍历’str1=‘根节点’+‘左子树的前序遍历’+‘右子树的前序遍历’,我可以知道这棵二叉树的根节点root便是str1的第一个字符!”小Ho道。
“而我在知道了‘根节点’root之后,我便可以利用‘中序遍历’str2=‘左子树的中序遍历’+‘根节点’+‘右子树的中序遍历’,求解出‘左子树的中序遍历’str2L和‘右子树的中序遍历’str2R!”
“接下来,由于一棵子树的前序遍历和中序遍历的长度相同,那么仍然是根据‘前序遍历’str1=‘根节点’+‘左子树的前序遍历’+‘右子树的前序遍历’,我可以知道从str1的第2个字符开始的str2L.length()个字符便是‘左子树的前序遍历’str1L,而这之后的部分便是‘右子树的前序遍历’str1R!”小Ho说到这里,顿了顿,希望从小Hi处得到些反馈。
“没错!那你准备如何求解post_order(str1, str2)呢?”小Hi肯定道。
“这只要根据之前求出的结果,和‘后序遍历’=‘左子树的后序遍历’+‘右子树的后序遍历’+‘根节点’,便可以知道——post_order(str1, str2)=post_order(str1l, str2l)+post_order(str1r, str2r)+root这样一个式子来!而这个问题的规模——也就是二叉树的大小,是一直在缩小的,所以是能够这样不断的划分做下去的!也就是说我之后可以将当前根节点的左子树又拆分成为两个问题来解决,一直到当前节点是叶子节点了为止!然后慢慢的将这些答案拼成上层的问题的答案,而这个过程只需要使用递归完成就可以了!”
“听起来很容易的样子呢!那你要不要赶紧去实现了算法,算出你的宝贝二叉树长什么样呢?”小Hi满意的点了点头,随即笑着问道。
“那是自然!”
输入
每个测试点(输入文件)有且仅有一组测试数据。
每组测试数据的第一行为一个由大写英文字母组成的字符串,表示该二叉树的前序遍历的结果。
每组测试数据的第二行为一个由大写英文字母组成的字符串,表示该二叉树的中序遍历的结果。
对于100%的数据,满足二叉树的节点数小于等于26。
输出
对于每组测试数据,输出一个由大写英文字母组成的字符串,表示还原出的二叉树的后序遍历的结果。
样例输入
AB BA
样例输出
BA
这题可以说是很微妙了,直接就把答案告诉你了。你直接转化成代码就好了
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
string post_order(string str1,string str2)
{
if(str1.length()<=0) return "";
//if(str1.length())
char c=str1[0];
int i=0,len=str2.length();
string str1l="",str2l="",str1r="",str2r="";
for(i=0;i<len;i++)
{
if(str2[i]==c)
break;
}
str2l=str2.substr(0,i);//cout<<str2l<<endl;
str2r=str2.substr(i+1);//cout<<str2r<<endl;
str1l=str1.substr(1,str2l.length());//cout<<str1l<<endl;
str1r=str1.substr(1+str2l.length());//cout<<str1r<<endl;
return post_order(str1l,str2l)+post_order(str1r,str2r)+c;
}
int main()
{
string a,b;
cin>>a>>b;
cout<<post_order(a,b)<<endl;
return 0;
}
1960: 单源最大权路径
http://acm.csu.edu.cn/csuoj/problemset/problem?pid=1960
Submit Page Summary Time Limit: 3 Sec Memory Limit: 128 Mb Submitted: 282 Solved: 134
Description
有一棵由N个结点构成的树,每一条边上都有其对应的权值。现在给定起点,求从该点出发的一条路径(至少有一条边)使得这条路径上的权值之和最大,并输出这个最大值。
Input
第一行一个正整数T,代表数据组数。每组数据第一行两个正整数n(2<=n<=10^5),s(1<=s<=n),分别表示树结点数目以及给定的起点,点的编号从1至N。接下来M行,每行三个整数x,y,z,(1<=x,y<=n,|z|<=1000),代表编号为x和y的点之间有一条权值为z的双向边。
Output
每组数据输出一行,即所找到路径的最大权值(格式参见样例)。
Sample Input
2 3 1 1 2 10 1 3 5 5 5 1 5 70 4 3 100 5 3 -10 2 5 60
Sample Output
Case #1: 10 Case #2: 90
Hint
Source
2017年6月月赛-暨中南大学暑期集训选拔赛第二场
Author
xushu
bfs+邻接表
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
const int size=1e5+5;
int first[size],nxt[size];
int flag[size];
struct node{
int b,e,v;
}edge[size];
int tot;
void roar_build(int id,int end,int value)
{
edge[tot].b=id;
edge[tot].e=end;
edge[tot].v=value;
nxt[tot]=first[id];
first[id]=tot++;
}
const int INF=0x3f3f3f3f;
int ans=0;
void dfs(int n,int vl)
{
int id;
if(first[n]==-1)
return ;
int val;
for(int i=first[n];i!=-1;i=nxt[i])
{
if(!flag[edge[i].e])
{
id=edge[i].e;
val=vl+edge[i].v;
ans=max(ans,val);
flag[edge[i].e]=1;
dfs(id,val);
flag[edge[i].e]=0;
}
}
}
int main()
{
int t;
cin>>t;
int cnt=0;
while(t--)
{
tot=0;
int s,n;
memset(nxt,0,sizeof(nxt));
memset(first,-1,sizeof(first));
memset(flag,0,sizeof(flag));
ans=-INF;
cin>>n>>s;
flag[s]=1;
for(int i=0;i<n-1;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
roar_build(x,y,z);
roar_build(y,x,z);
}
dfs(s,0);
printf("Case #%d: ",++cnt);
cout<<ans<<endl;
}
return 0;
}
N皇后问题
http://acm.hdu.edu.cn/showproblem.php?pid=2553
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 32936 Accepted Submission(s): 14174
Problem Description
在N*N的方格棋盘放置了N个皇后,使得它们不相互攻击(即任意2个皇后不允许处在同一排,同一列,也不允许处在与棋盘边框成45角的斜线上。
你的任务是,对于给定的N,求出有多少种合法的放置方法。
Input
共有若干行,每行一个正整数N≤10,表示棋盘和皇后的数量;如果N=0,表示结束。
Output
共有若干行,每行一个正整数,表示对应输入行的皇后的不同放置数量。
Sample Input
1 8 5 0
Sample Output
1 92 10
Author
cgf
Source
dfs入门题,时间卡的好紧,所以先处理出答案记录入数组。
#include<stdio.h>
int n,locat[11];
long long solve;
void check(int x)
{
int i,ok,q;
if(x==n) solve++;
else for(i=0;i<n;i++)
{
ok=1;
locat[x]=i;
for(q=0;q<x;q++)
{
if(locat[x]==locat[q]||x-locat[x]==q-locat[q]||locat[x]+x==locat[q]+q)
{ok=0;break;}
}
if(ok==1)
check(x+1);
}
}
int main()
{
int solv[11]={0,1,0,0,2,10,4,40,92,352,724};
while(~scanf("%d",&n))
{
if(n==0) break;
printf("%d\n",solv[n]);
}
}
Prime Ring Problem
http://acm.hdu.edu.cn/showproblem.php?pid=1016
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 64943 Accepted Submission(s): 27877
Problem Description
A ring is compose of n circles as shown in diagram. Put natural number 1, 2, ..., n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.
Note: the number of first circle should always be 1.
Input
n (0 < n < 20).
Output
The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.
You are to write a program that completes above process.
Print a blank line after each case.
Sample Input
6 8
Sample Output
Case 1: 1 4 3 2 5 6 1 6 5 2 3 4 Case 2: 1 2 3 8 5 6 7 4 1 2 5 8 3 4 7 6 1 4 7 6 5 8 3 2 1 6 7 4 3 8 5 2
Source
Asia 1996, Shanghai (Mainland China)
素数环问题,经典dfs入门,需要注意的是最后需要判断最后一个与第一个的关系
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
int arr[25];
int flag[25];
int n;
int check[]={1,3,5,7,11,13,17,19,23,29,31,37};
void pr()
{
int i=0;
for(i;i<n;i++)
{
printf("%d",arr[i]);
if(i!=n-1)
printf(" ");
else printf("\n");
}
}
int ok(int x,int y)
{
int z=x+y;
int flag=0;
for(int i=0;i<12;i++)
{
if(z==check[i]) flag=1;
}
return flag;
}
void dfs(int depth)
{
if(depth==n)
{
if(ok(arr[depth-1],1))
pr();
return;
}
else{
for(int i=0;i<12;i++)
{
int u=check[i]-arr[depth-1];
if(u>0&&!flag[u]&&u<=n)
{
flag[u]=1;
arr[depth]=u;
dfs(depth+1);
flag[u]=0;
}
}
}
}
int main()
{
int cnt=0;
while(cin>>n)
{
memset(flag,0,sizeof(flag));
flag[1]=1;
arr[0]=1;
printf("Case %d:\n",++cnt);
dfs(1);
printf("\n");
}
return 0;
}
Robot Motion
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 13573 Accepted Submission(s): 6327
Problem Description

A robot has been programmed to follow the instructions in its path. Instructions for the next direction the robot is to move are laid down in a grid. The possible instructions are
N north (up the page)
S south (down the page)
E east (to the right on the page)
W west (to the left on the page)
For example, suppose the robot starts on the north (top) side of Grid 1 and starts south (down). The path the robot follows is shown. The robot goes through 10 instructions in the grid before leaving the grid.
Compare what happens in Grid 2: the robot goes through 3 instructions only once, and then starts a loop through 8 instructions, and never exits.
You are to write a program that determines how long it takes a robot to get out of the grid or how the robot loops around.
Input
There will be one or more grids for robots to navigate. The data for each is in the following form. On the first line are three integers separated by blanks: the number of rows in the grid, the number of columns in the grid, and the number of the column in which the robot enters from the north. The possible entry columns are numbered starting with one at the left. Then come the rows of the direction instructions. Each grid will have at least one and at most 10 rows and columns of instructions. The lines of instructions contain only the characters N, S, E, or W with no blanks. The end of input is indicated by a row containing 0 0 0.
Output
For each grid in the input there is one line of output. Either the robot follows a certain number of instructions and exits the grid on any one the four sides or else the robot follows the instructions on a certain number of locations once, and then the instructions on some number of locations repeatedly. The sample input below corresponds to the two grids above and illustrates the two forms of output. The word "step" is always immediately followed by "(s)" whether or not the number before it is 1.
Sample Input
3 6 5 NEESWE WWWESS SNWWWW 4 5 1 SESWE EESNW NWEEN EWSEN 0 0
Sample Output
10 step(s) to exit 3 step(s) before a loop of 8 step(s)
Source
简单dfs
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
using namespace std;
char map[11][11];
int flag[11][11];
int situ[11][11];
int sx,sy,b;
int check(int x,int y)
{
if(x>sx||x<1||y>sy||y<1)
return 0;
return 1;
}
void dfs(int x,int y,int befo)
{
if(check(x,y))
{
if(flag[x][y])
{
cout<<situ[x][y]-1<<" step(s) before a loop of "<<befo-situ[x][y]+1<<" step(s)"<<endl;
return;
}
}
else
{
cout<<befo<<" step(s) to exit"<<endl;
return;
}
situ[x][y]=befo+1;
//cout<<situ[x][y]<<' '<<befo<<endl;
flag[x][y]=1;
if(map[x][y]=='N') dfs(x-1,y,situ[x][y]);
if(map[x][y]=='S') dfs(x+1,y,situ[x][y]);
if(map[x][y]=='E') dfs(x,y+1,situ[x][y]);
if(map[x][y]=='W') dfs(x,y-1,situ[x][y]);
}
int main()
{
while(~scanf("%d%d",&sx,&sy))
{
if(!sx) break;
cin>>b;
memset(situ,0,sizeof(situ));
memset(flag,0,sizeof(flag));
int i;
for(i=1;i<=sx;i++)
{
scanf("%s",map[i]+1);
}
dfs(1,b,0);
//cout<<"x"<<endl;
}
return 0;
}|
Avoid The Lakes http://poj.org/problem?id=3620
Description Farmer John's farm was flooded in the most recent storm, a fact only aggravated by the information that his cows are deathly afraid of water. His insurance agency will only repay him, however, an amount depending on the size of the largest "lake" on his farm. Input * Line 1: Three space-separated integers: N, M, and K Output * Line 1: The number of cells that the largest lake contains. Sample Input Sample Output Source |
dfs对全图遍历,取出所有的块的大小,取其中最大的
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
using namespace std;
int map[105][105];
int flag[105][105];
int x0[10005],y0[10005];
int n,m,k;
int mov[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
int check(int x,int y)
{
if(x>=1&&x<=n&&y>=1&&y<=m&&!flag[x][y]&&map[x][y]) return 1;
else return 0;
}
int dfs(int x,int y)
{
int s=0;
int sign=0;
flag[x][y]=1;
for(int i=0;i<4;i++)
{
int xx,yy;
xx=x+mov[i][0];
yy=y+mov[i][1];
if(check(xx,yy))
{
sign=1;
s+=dfs(xx,yy);
}
}
if(!sign)return 1;
return s+1;
}
int main()
{
while(cin>>n>>m>>k)
{
memset(map,0,sizeof(map));
memset(flag,0,sizeof(flag));
int ans=0;
for(int i=0;i<k;i++)
{
scanf("%d%d",&x0[i],&y0[i]);
map[x0[i]][y0[i]]=1;
}
for(int i=0;i<k;i++)
{
if(!flag[x0[i]][y0[i]])
{
ans=max(ans,dfs(x0[i],y0[i]));
}
//cout<<endl;
}
cout<<ans<<endl;
}
return 0;
}


