暑假训练DAY7(计算几何)
B - 直线相交
We all know that a pair of distinct points on a plane defines a line and that a pair of lines on a plane will intersect in one of three ways: 1) no intersection because they are parallel, 2) intersect in a line because they are on top of one another (i.e. they are the same line), 3) intersect in a point. In this problem you will use your algebraic knowledge to create a program that determines how and where two lines intersect.
Your program will repeatedly read in four points that define two lines in the x-y plane and determine how and where the lines intersect. All numbers required by this problem will be reasonable, say between -1000 and 1000.
Input
The first line contains an integer N between 1 and 10 describing how many pairs of lines are represented. The next N lines will each contain eight integers. These integers represent the coordinates of four points on the plane in the order x1y1x2y2x3y3x4y4. Thus each of these input lines represents two lines on the plane: the line through (x1,y1) and (x2,y2) and the line through (x3,y3) and (x4,y4). The point (x1,y1) is always distinct from (x2,y2). Likewise with (x3,y3) and (x4,y4).
Output
There should be N+2 lines of output. The first line of output should read INTERSECTING LINES OUTPUT. There will then be one line of output for each pair of planar lines represented by a line of input, describing how the lines intersect: none, line, or point. If the intersection is a point then your program should output the x and y coordinates of the point, correct to two decimal places. The final line of output should read "END OF OUTPUT".
Sample Input
5 0 0 4 4 0 4 4 0 5 0 7 6 1 0 2 3 5 0 7 6 3 -6 4 -3 2 0 2 27 1 5 18 5 0 3 4 0 1 2 2 5
Sample Output
INTERSECTING LINES OUTPUT POINT 2.00 2.00 NONE LINE POINT 2.00 5.00 POINT 1.07 2.20 END OF OUTPUT
模板题
先判断时候平行,如平行再判断是重合还是相离
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
const double pi=acos(-1.0);
struct Point{
double x,y;
Point(double x=0,double y=0):x(x),y(y){
}
};//点的结构体
typedef Point Vector;//同时也是向量
Vector operator+(Vector a,Vector b) {return Vector(a.x+b.x,a.y+b.y);}//向量相加
Vector operator-(Vector a,Vector b) {return Vector(a.x-b.x,a.y-b.y);}//向量相减 ,得到向量ba
Vector operator*(Vector a,double b) {return Vector(a.x*b,a.y*b);}//向量乘上一个数
Vector operator/(Vector a,double b) {return Vector(a.x/b,a.y/b);}//向量除去一个数
bool operator< (const Point &a,const Point &b)
{
return a.x<b.x||(a.x==b.x&&a.y<b.y);
}//方便对点进行排序,依据的排序规则为水平坐标小的就小一些,当水平坐标相等时就纵坐标小的小
const double eps=1e-10;//可以适当调整为1e-8
int dcmp(double x)
{
if(fabs(x)<eps) return 0;
if(x<0) return -1;
return 1;
}
bool operator==(const Point &a,const Point &b)
{
return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;//对向量(点)的相等进行重载
}
/*********************************************
向量之间的一些基本运算
*********************************************/
//向量与向量的计算
double Dot(Vector a,Vector b)
{
return a.x*b.x+a.y*b.y;//向量的点乘
}
double Length(Vector a)
{
return sqrt(Dot(a,a));//计算向量a的长度
}
double Angle(Vector a,Vector b)
{
return acos(Dot(a,b) / Length(a) / Length(b));//计算向量a,b的夹角
}
double Cross(Vector a,Vector b)
{
return a.x*b.y-a.y*b.x;
//计算a×b,切记,叉乘有前后之分
//b的在a的逆时针方向时为正
}
double Area2(Point a,Point b,Point c)
{
return Cross(b-a,c-a);
//计算a,b,c三点构成的三角形的面积的两倍
//注意:ab(由a指向b的向量),ac(a指向c的向量)。
//ac在ab的逆时针方向时,面积为正,反之为负
}
Vector Rotate(Vector a,double rad)
{
return Vector(a.x*cos(rad)-a.y*sin(rad),a.x*sin(rad)+a.y*cos(rad));
//rad是弧度,旋转方向为逆时针
}
Vector Normal(Vector a)
{
double L=Length(a);
return Vector(-a.y/L,a.x/L);
//求出a向量的单位法向量
//逆时针旋转90度的法向量
}
Point GetLineIntersection(Point p,Vector v,Point q,Vector w)
{
Vector u=p-q;
double t=Cross(w,u)/Cross(v,w);
return p+v*t;
//返回直线p+tv和q+tw的交点(v,w分别是两条线的方向向量,p和q分别是直线上的一点)
//需要注意的是Cross(v,w)不能共线
}
double Distancetoline(Point p,Point a,Point b)
{
Vector v1=b-a,v2=p-a;
return fabs(Cross(v1,v2))/Length(v1);
//求得p到直线ab的距离
}
double Distancetosegment(Point p,Point a,Point b)
{
if(a==b) return Length(p-a);
Vector v1=b-a,v2=p-a,v3=p-b;
if(dcmp(Dot(v1,v2))<0) return Length(v2);
if(dcmp(Dot(v1,v3))>0) return Length(v3);
return fabs(Cross(v1,v2))/Length(v1);
//求得p到直线ab的最小距离
}
Point GetLineProjection(Point p,Point a,Point b)
{
Vector v=b-a;
return a+v*(Dot(v,p-a) /Dot(v,v));
//p在直线ab上的投影点
}
int SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2)
{
double c1=Cross(a2-a1,b1-a1),c2=Cross(a2-a1,b2-a1),
c3=Cross(b2-b1,a1-b1),c4=Cross(b2-b1,a2-a1);
if(c1==0&&c2==0) return -1;
return dcmp(c1)*dcmp(c2)<0&&dcmp(c3)*dcmp(c4)<0;
//判断a1a2与b1b2是否相交(交点不在a1,a2,b1,b2上)
//如果c1c2同时为0表示两直线共线
}
//当c1c2不同时为零时,还有一种一条线段在;另一条直线上的端点的情况,需要用下函数判断某点是否在直线上
bool OnSegment(Point p,Point a1,Point a2)
{
return dcmp(Cross(a1-p,a2-p))==0&&dcmp(Dot(a1-p,a2-p))<0;
//用叉乘判断时候在这条直线上,用点乘判断是否在线段中
//判断p点是否在线段a1a2上
}
int main()
{
int t;
cin>>t;
cout<<"INTERSECTING LINES OUTPUT"<<endl;
while(t--)
{
double x1,y1,x2,y2;
double x3,y3,x4,y4;
cin>>x1>>y1>>x2>>y2;
cin>>x3>>y3>>x4>>y4;
Point a1(x1,y1),b1(x3,y3),a2(x2,y2),b2(x4,y4);
Vector va(x2-x1,y2-y1),vb(x4-x3,y4-y3);
int sign;
if(dcmp(Cross(va,vb))==0)
{
if(dcmp(Distancetoline(a1,b1,b2))==0)
{
sign=-1;
}
else sign=0;
}
else sign=1;
if(sign==-1) cout<<"LINE"<<endl;
if(sign==0) cout<<"NONE"<<endl;
if(sign==1) {
cout<<"POINT ";Point u=GetLineIntersection(a1,va,b1,vb);
printf("%.2f %.2f\n",u.x,u.y);
}
}
cout<<"END OF OUTPUT"<<endl;
return 0;
}C - 凸包模版
The small sawmill in Mission, British Columbia, has developed a brand new way of packaging boards for drying. By fixating the boards in special moulds, the board can dry efficiently in a drying room.
Space is an issue though. The boards cannot be too close, because then the drying will be too slow. On the other hand, one wants to use the drying room efficiently.
Looking at it from a 2-D perspective, your task is to calculate the fraction between the space occupied by the boards to the total space occupied by the mould. Now, the mould is surrounded by an aluminium frame of negligible thickness, following the hull of the boards' corners tightly. The space occupied by the mould would thus be the interior of the frame.
Input
On the first line of input there is one integer, N< = 50, giving the number of test cases (moulds) in the input. After this line,N test cases follow. Each test case starts with a line containing one integern,1< n <= 600, which is the number of boards in the mould. Thenn lines follow, each with five floating point numbersx, y, w, h, j where0 <= x, y, w, h <=10000 and –90° <j< =90°. The x and y are the coordinates of the center of the board andw andh are the width and height of the board, respectively.j is the angle between the height axis of the board to they-axis in degrees, positive clockwise. That is, ifj = 0, the projection of the board on thex-axis would bew. Of course, the boards cannot intersect.
Output
For every test case, output one line containing the fraction of the space occupied by the boards to the total space in percent. Your output should have one decimal digit and be followed by a space and a percent sign (%).
Sample Input
|
1 4 4 7.5 6 3 0 8 11.5 6 3 0 9.5 6 6 3 90 4.5 3 4.4721 2.2361 26.565 |
Output for Sample Input
64.3 %
先用凸包模板求出凸包边界的点,再用多边形面积模板求出多边形的面积
也是对着白书上打的。。
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
const double pi=acos(-1.0);
struct Point{
double x,y;
Point(double x=0,double y=0):x(x),y(y){
}
};//点的结构体
typedef Point Vector;//同时也是向量
Vector operator+(Vector a,Vector b) {return Vector(a.x+b.x,a.y+b.y);}//向量相加
Vector operator-(Vector a,Vector b) {return Vector(a.x-b.x,a.y-b.y);}//向量相减 ,得到向量ba
Vector operator*(Vector a,double b) {return Vector(a.x*b,a.y*b);}//向量乘上一个数
Vector operator/(Vector a,double b) {return Vector(a.x/b,a.y/b);}//向量除去一个数
bool operator< (const Point &a,const Point &b)
{
return a.x<b.x||(a.x==b.x&&a.y<b.y);
}//方便对点进行排序,依据的排序规则为水平坐标小的就小一些,当水平坐标相等时就纵坐标小的小
const double eps=1e-10;//可以适当调整为1e-8
int dcmp(double x)
{
if(fabs(x)<eps) return 0;
if(x<0) return -1;
return 1;
}
bool operator==(const Point &a,const Point &b)
{
return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;//对向量(点)的相等进行重载
}
Vector Rotate(Vector a,double rad)
{
return Vector(a.x*cos(rad)-a.y*sin(rad),a.x*sin(rad)+a.y*cos(rad));
//rad是弧度,旋转方向为逆时针
}
double Cross(Vector a,Vector b)
{
return a.x*b.y-a.y*b.x;
//计算a×b,切记,叉乘有前后之分
//b的在a的逆时针方向时为正
}
int ConvexHull(Point* p,int n,Point* ch)
{
//输入点数组p,个数n,输出点数组ch,函数返回凸包的顶点数量
//输入点钟不能有重复点
//函数执行完成后p的顺序将会被破坏
// 如果在凸包的边界上不希望出现输入的点的话把两个<=改成<
//精度高时采用dcmp比较
sort(p,p+n);
int m=0;
for(int i=0;i<n;i++)
{
while(m>1&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--;
ch[m++]=p[i];
}
int k=m;
for(int i=n-2;i>=0;i--)
{
while(m>k&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--;
ch[m++]=p[i];
}
if(n>1) m--;
return m;
}
double PolygonArea(Point* p,int n)
{
double area=0;
for(int i=1;i<n-1;i++)
{
area+=Cross(p[i]-p[0],p[i+1]-p[0]);
}
return area/2;
//注意此方法的得出的面积有向,在不能保证点的分布是顺时针还是啊逆时针的时候需要加上绝对值
//p是点的数组,n是多边形的边数,也是点数
}
Point p[2500],ch[2500];
int main()
{
int t;
cin>>t;
while(t--)
{
int n,pc=0;
double area1=0;
cin>>n;
for(int i=0;i<n;i++)
{
double x,y,w,h,ang;
cin>>x>>y>>w>>h>>ang;
Point o(x,y);
ang=-(ang/180*pi);
p[pc++]=o+Rotate(Vector(-w/2,-h/2),ang);
p[pc++]=o+Rotate(Vector(w/2,-h/2),ang);
p[pc++]=o+Rotate(Vector(-w/2,h/2),ang);
p[pc++]=o+Rotate(Vector(w/2,h/2),ang);
area1+=w*h;
}
int m=ConvexHull(p,pc,ch);
double area2=PolygonArea(ch,m);
printf("%.1f %%\n",area1*100/area2);
}
return 0;
}Area
http://poj.org/problem?id=1654
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 21440 | Accepted: 5819 |
Description
You are going to compute the area of a special kind of polygon. One vertex of the polygon is the origin of the orthogonal coordinate system. From this vertex, you may go step by step to the following vertexes of the polygon until back to the initial vertex. For each step you may go North, West, South or East with step length of 1 unit, or go Northwest, Northeast, Southwest or Southeast with step length of square root of 2.
For example, this is a legal polygon to be computed and its area is 2.5:
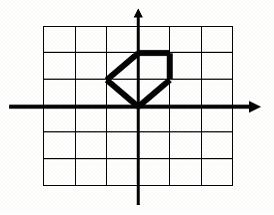
Input
The first line of input is an integer t (1 <= t <= 20), the number of the test polygons. Each of the following lines contains a string composed of digits 1-9 describing how the polygon is formed by walking from the origin. Here 8, 2, 6 and 4 represent North, South, East and West, while 9, 7, 3 and 1 denote Northeast, Northwest, Southeast and Southwest respectively. Number 5 only appears at the end of the sequence indicating the stop of walking. You may assume that the input polygon is valid which means that the endpoint is always the start point and the sides of the polygon are not cross to each other.Each line may contain up to 1000000 digits.
Output
For each polygon, print its area on a single line.
Sample Input
4 5 825 6725 6244865
Sample Output
0 0 0.5 2
Source
POJ Monthly--2004.05.15 Liu Rujia@POJ
求出运动路径的点,然后用多边形面积模板做就行了
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
const double pi=acos(-1.0);
struct Point{
int x,y;
Point(int x=0,int y=0):x(x),y(y){
}
};//点的结构体
typedef Point Vector;//同时也是向量
Vector operator-(Vector a,Vector b) {return Vector(a.x-b.x,a.y-b.y);}//向量相减 ,得到向量ba
long long Cross(Vector a,Vector b)
{
return a.x*b.y-a.y*b.x;
//计算a×b,切记,叉乘有前后之分
//b的在a的逆时针方向时为正
}
long long PolygonArea(Point* p,int n)
{
long long area=0;
for(int i=1;i<n-1;i++)
{
area+=Cross(p[i]-p[0],p[i+1]-p[0]);
}
return area;
//注意此方法的得出的面积有向,在不能保证点的分布是顺时针还是啊逆时针的时候需要加上绝对值
//p是点的数组,n是多边形的边数,也是点数
}
Point px[1000005];
map<char,int> mvx;
map<char,int> mvy;
void init()
{
mvx['8']=0,mvy['8']=1;
mvx['2']=0,mvy['2']=-1;
mvx['6']=1,mvy['6']=0;
mvx['4']=-1,mvy['4']=0;
mvx['9']=1,mvy['9']=1;
mvx['7']=-1,mvy['7']=1;
mvx['3']=1,mvy['3']=-1;
mvx['1']=-1,mvy['1']=-1;
mvx['5']=0,mvy['5']=0;
}
int main()
{
int t;
cin>>t;
init();
while(t--)
{
memset(px,0,sizeof(px));
string str;
cin>>str;
px[0].x=0,px[0].y=0;
for(int i=1;i<str.length();i++)
{
Point nxt;
nxt.x=px[i-1].x+mvx[str[i-1]];
nxt.y=px[i-1].y+mvy[str[i-1]];
px[i]=nxt;
}
long long ans=fabs(PolygonArea(px,str.length()));
printf("%lld",ans/2);
if(ans&1) printf(".5");
printf("\n");
}
return 0;
}这里附上我的计算几何的模板的链接:


