Ultra-QuickSort POJ - 2299 （归并排序求逆序对（带原理简介））

In this problem, you have to analyze a particular sorting algorithm. The algorithm processes a sequence of n distinct integers by swapping two adjacent sequence elements until the sequence is sorted in ascending order. For the input sequence 

9 1 0 5 4 ,

Ultra-QuickSort produces the output 

0 1 4 5 9 .

Your task is to determine how many swap operations Ultra-QuickSort needs to perform in order to sort a given input sequence.

Input

The input contains several test cases. Every test case begins with a line that contains a single integer n < 500,000 -- the length of the input sequence. Each of the the following n lines contains a single integer 0 ≤ a[i] ≤ 999,999,999, the i-th input sequence element. Input is terminated by a sequence of length n = 0. This sequence must not be processed.

Output

For every input sequence, your program prints a single line containing an integer number op, the minimum number of swap operations necessary to sort the given input sequence.

Sample Input

5
9
1
0
5
4
3
1
2
3
0

Sample Output

6
0

题意说的很明白了就是简单地求逆序对。当然也可以使用树状数组加离散化来处理，但是这里我们选择更加好写的归并排序来写

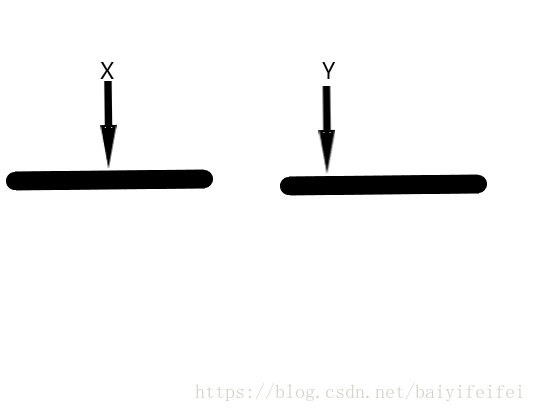
归并排序求逆序对原理简介：

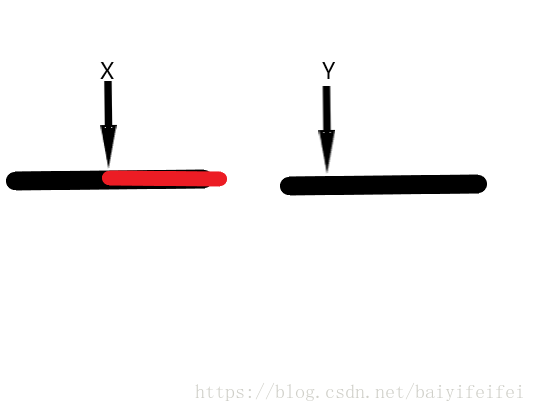
假设我们手头有两个已经从小到大排好序的数组，且他们分别是原来的一段大数组的前半段和后半段，现在我们的比较到了x,y位置

假使X>Y则其必然构成一对逆序对，与此同时我所画出的红色的这一段的的数均大于Y，所以逆序对的数量就要加上这一段的长度

而对整个数组都归并排序完毕后最终就可以得到逆序对的和

附带上一个逆序对的模板（大佬小伙伴写的）

int A[100010];//输入的任意序列
int T[100010];//临时空间
long long cnt;
void merge_sort(int *A,int x,int y,int *T)
{
	if(y-x>1)//如果序列非空
	{								05
		int m=x+(y-x)/2;//如果序列长度为奇数左边序列比右边少一个,如果偶数则一样
		int p=x,q=m,i=x;//p,q是当前左右序列第一个元素的位置（最小的那个）
		merge_sort(A,x,m,T);//递归排序
		merge_sort(A,m,y,T);
		while(p<m || q<y)//只要有一个序列非空就继续合并
		{
			if(q>=y || p<m&&A[p]<=A[q]) T[i++]=A[p++];//如果右边或左边非空且左边第一个元素小与右边第一个，
											//就把左边那个加到临时空间里
			else 
				{
					T[i++]=A[q++];
					cnt+=m-p;//	逆序数
				}
		}
		for(i=x;i<y;i++) A[i]=T[i];//把排序好的T复制回A，A的范围是[x,y)
	}
}

AC代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#define endl '\n'
#define sc(x) scanf("%lld",&x)
#define md(a,b) a+(b-a)/2
using namespace std;
typedef long long LL;
const int size=5e5+5;
LL arr[size],Temp[size];
LL ans=0;
void  MergeSort(int x,int y)
{
	if(y-x>1)
	{
		int m=md(x,y);
		int p=x,q=m,i=x;
		MergeSort(x,m);
		MergeSort(m,y);
		while(p<m||q<y)
		{
			if(q>=y|| p<m&&arr[p]<=arr[q]) Temp[i++]=arr[p++];
			else
			{
				Temp[i++]=arr[q++];
				ans+=(m-p);
			}
		}
		for(int i=x;i<y;i++) arr[i]=Temp[i];
	}
}
int main()
{
	int n;
	while(~scanf("%d",&n)&&n)
	{
		memset(arr,0,sizeof(arr));
		memset(Temp,0,sizeof(Temp));
		ans=0;
		for(int i=0;i<n;i++)
		{
			sc(arr[i]);
		}
		MergeSort(0,n);
		cout<<ans<<endl;
	}
	return 0;
}