【找规律】bzoj 1002: [FJOI2007]轮状病毒
1002: [FJOI2007]轮状病毒
Description
轮状病毒有很多变种,所有轮状病毒的变种都是从一个轮状基产生的。一个N轮状基由圆环上N个不同的基原子
和圆心处一个核原子构成的,2个原子之间的边表示这2个原子之间的信息通道。如下图所示
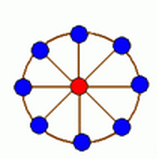
N轮状病毒的产生规律是在一个N轮状基中删去若干条边,使得各原子之间有唯一的信息通道,例如共有16个不
同的3轮状病毒,如下图所示

现给定n(N<=100),编程计算有多少个不同的n轮状病毒
Input
第一行有1个正整数n
Output
计算出的不同的n轮状病毒数输出
Sample Input
3
Sample Output
16
题解
题意
如上述意,不再赘述
思路
据打表
我们会发现奇数项似乎都可以分解为一个数的平方
1,4,11,29,76,199
将其单独作为一个数列我们就会得到递推式
再来观察偶数项,偶数项(除了第二项)似乎都可以分解为5乘上一个数的平方,而数为:
3,8,21,55
将其单独作为一个数列我们又可以得到递推式
据此,我们既可以得到整个序列,由于答案较大,所以需要用到大数,这里使用的是JAVA
AC代码
/**************************************************************
Problem: 1002
User: FlyWhite
Language: Java
Result: Accepted
Time:1028 ms
Memory:17864 kb
****************************************************************/
import java.math.BigInteger;
import java.util.Scanner;
public class Main
{
public static void main(String[] args)
{
BigInteger[] a = new BigInteger[105];
BigInteger[] b = new BigInteger[105];
BigInteger[] ans = new BigInteger[105];
a[1] = BigInteger.valueOf(1);
a[2] = BigInteger.valueOf(3);
for(int i = 3;i <= 99;++i)
a[i] = a[i-1].add(a[i-2]);
b[2] = BigInteger.valueOf(3);
b[4] = BigInteger.valueOf(3);
b[5] = BigInteger.valueOf(5);
for(int i = 6;i <= 100;++i)
b[i] = b[i-1].add(b[i-2]);
for(int i = 1;i <= 99;i += 2)
ans[i] = a[i].multiply(a[i]);
ans[2] = b[2];
for(int i = 4;i <= 100;i += 2)
ans[i] = b[i].multiply(b[i]).multiply(BigInteger.valueOf(5));
int n;
Scanner input = new Scanner(System.in
);
while(input.hasNext())
{
n = input.nextInt();
System.out.println(ans[n]);
}
}
}



