[Reinforcement Learning]Lecture 8:Integrating Learning and Planning
[Reinforcement Learning]Lecture 8:Integrating Learning and Planning
Outline
- 本章的一些概念的介绍
- integrated Architectures(集合learning与planning)
- 基于仿真的搜索
介绍
基于模型的强化学习
在之前的课程中我们已经学习过了通过experience 学习策略和值函数,在本节中我们要直接通过experience学习得model(模型),而通过planning来构造出值函数或者说是策略。通过整合learning和planing的方法来得到一个简单的结构
前情提要:
什么是planning?
planning
从Model中生成或提升Policy 的计算过程称为 Planning,如DP就是基于planning得到的
由于learning,planning都满足通过计算values function 来进行Policy 提升,这表示很多思想和算法可以相互借鉴,在应用中常常用learning 中value function 估计值的更新公式取代Planning中的value function 估计值的更新公式。例如,我们可以将Q learning 和 planning 结合,得到random-sample one-step tabular Q-planning 方法():
基于模型和无模型的RL
无模型的RL
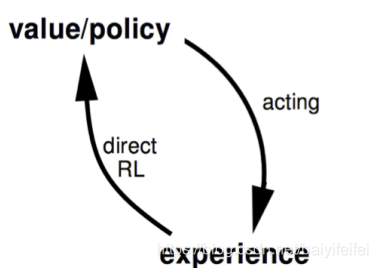
这种方法不存在模型,其直接从真实的experience中学习(learning)值函数(或是策略),如MC,TD就是基于这种方法的
用状态转移图来表示就是
基于模型的RL
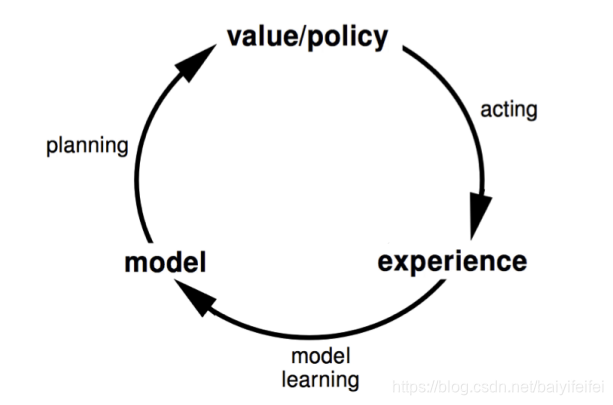
这种方法通过experience学习出一个模型,再通过这个模型来规划(planning)得值函数(或是策略),如DP就是基于这种方法的
用状态转移图来表示就是
整合架构
引出
让我们来考虑一个问题,假如我们现在所有的experience有两个来源,一部分来自于对应环境的直接采样,即真正的experience ,和来自于对于模型的采样,那么我们应该如何选择RL的方法呢?
结合学习(learning)与规划(planning)
我们通过结合无模型方法和有模型方法得到了Dyna方法
Dyna
与基于模型的RL相同,我们通过真正的experience 来学习得模型
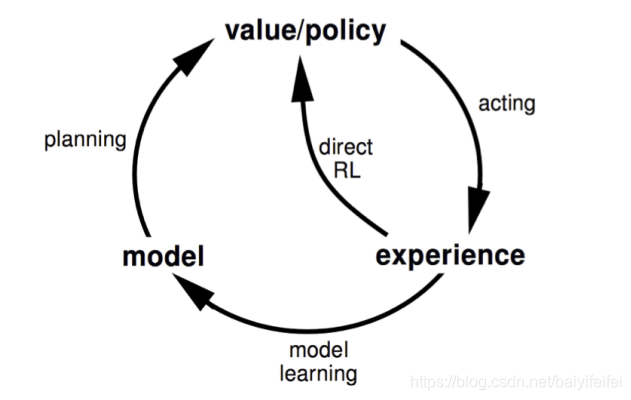
但是同时通过由对环境直接采样得到的真正的experience 来学习,和通过对模型的采样得到的近似的experience来规划得值函数(或策略)
用状态转移图来表示就是
具体介绍Dyna算法
图示
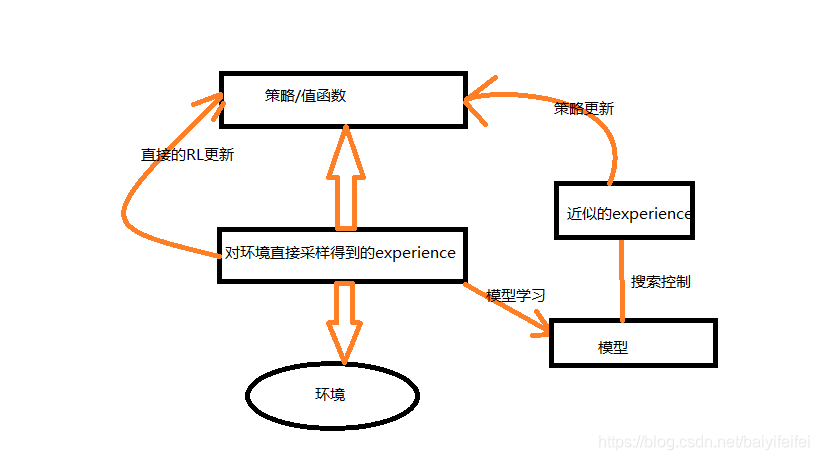
其中,中轴线为agent与环境交互的过程,会生成一系列的 直接采样得到的 experience,也是real experience,左侧直接RL 利用 real experience 提升 value function 和Policy。右侧,模型学习 利用 real experience 来对环境建模生成model,搜索控制 表示从model中选择初始态和 动作来生成的近似experience 的过程,最后,规划对近似 experience 运用强化学习方法。
组成
Dyna-Q 依次包括了Planning, acting, model learning, direct RL 等过程。其中,Planning方法为上文提到的random-sample one-step tabular Q-planning,direct RL方法为 one-step tabular Q-learning,model learning也是一种 table-based 方法,这里我们假设环境是确定的(即在一个确定状态下选择一个确定的动作必然会到达另一个确定的状态)。
在Dyna-Q中,one-step Q-learning分别被用于 学习 和规划 ,区别在于学习 (此处为直接RL)中单步 Q-learning的作用对象为 real experience, 而在规划 中,单步 Q-planning的作用对象为 simulated experience。
代码实现
从概念上而言,Planning, acting, model learning, direct RL应该是同步进行的,但在实际运用中,acting, model learning, direct RL所占用的计算资源远小于Planning,所以调整了他们的执行顺序,先执行acting, model learning, direct RL,再进行几步Planning,以Dyna-Q为例,算法伪代码如下:

其中a-e为直接通过real experience来RL,而f为planning的,其中n的大小即planning的次数
举个例子
以迷宫问题为例
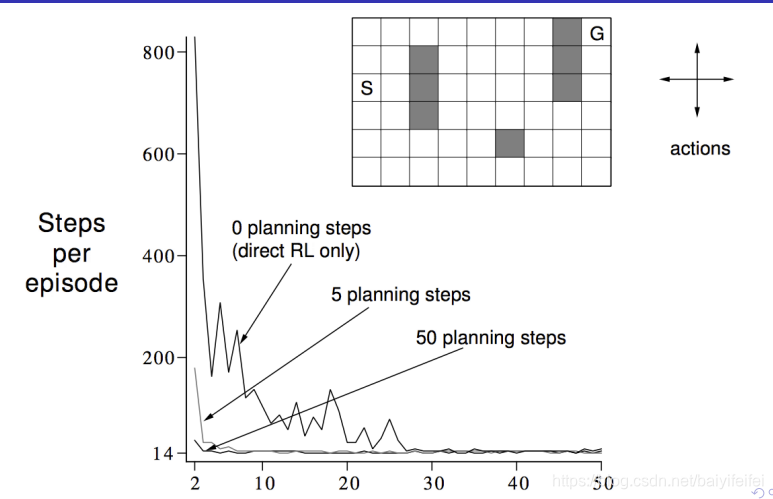
我们可以发现规划的次数越大,则越快地可以达到收敛。
在错误模型下的Dyna-Q
在真正的实验中,我们并不总能得到正确的模型,因为:
- 环境是随机的,且仅仅有一部分数据可以被观测到
- 用function approximate(函数逼近)学到的model不完美
- 环境在变化,新的行为没有被检测到
而假如当model 不正确时,Planning 往往会陷入局部最优。
为此我们进一步提出了Dyna-Q+方法
Dyna-Q+
Dyna-Q+在Dyna-Q的基础上,对每组state-action 距离自身最近一次出现的消失时间进行了统计,然后认为消失时间越久的state-action越容易发生变化,他的model就越可能出错。
为了鼓励算法去探索那些长时间没有尝试的action,定义一个bonus reward:如果model的reward 为 r, 一组state-action 有 ττ 个时间没有出现,那么这组state-action 的reward为 。其中,k为一个较小的系数。在shortcut maze中,Dyna-Q+的表现比Dyna-Q 好。
举例说明
Shortcut Maze
初始时刻环境如左图所示,最优策略为沿着左侧行走,3000步后,环境发生变化,原始最优策略的路径仍然可以通行,在此基础上开辟了一条新的路径,比原始最优路径好。但是实验结果显示 Dyna-Q的return曲线没有明显的波折,表明 Dyna-Q并没有发现model的错误。
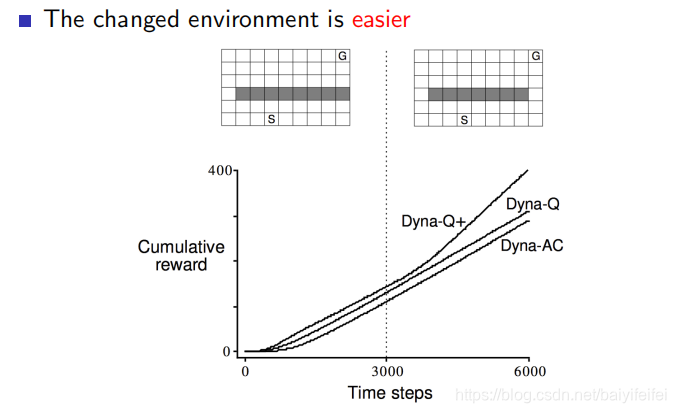
基于仿真的搜索
引入
上文中,我们提到了可以通过在learning中结合入planning来提高RL收敛的速率,这里我们来介绍两种planning
-background Planning 一种是我们前面一直在说的基于model产生的simulated experience用以逐步提升Policy 或 value function的Planning。通过比较当前state下的value,来选择action。在当前state下,选择action之前,Planning重点在于提高value表或者value 的近似函数表达,涉及到为很多state选择action。此处,Planning所关注的不是当前state。
-decision-time Planning 每给出一个新的state就立即规划出一个action,这种Planning方式比one-step-ahead 方式更深入。通常这种Planning方式多用在不需要快速回应的任务中,如下象棋,可以允许有一定的决策时间。
而在decision-time Planning中,Monte Carlo Tree Search(MCTS) 就是其中特别优秀的一种
Monte Carlo Tree Search(MCTS)
在棋类游戏中,构建博弈树之后使用alpha-beta剪枝来进行搜索经常是一种非常常用的方法,但是MCTS在实际中通常具有更好的灵活性。
以棋类游戏为例。我们需要建立一棵以当前状态为根节点,action为边,后继状态为其余节点,最终一方胜利为叶子节点的搜索树。其核心搜索过程大致上可以分为如下的四步:
- 选择:从已知的状态中选出一个最具‘价值’的状态,此价值由状态的‘重要性’决定,由此状态创建一个节点
- 扩展:在第一个节点上随机扩出一个或者多个节点
- 仿真:在第二步扩散出的节点中选择一个,采用某种策略随机的方法生成新的状态,并在这个新的状态上继续利用这个随即策略生成新的状态直至到达根节点
- 回传:将最终的结果的结果回传给其路径上的其他点
伪代码如下
function MCTS
创建节点 V0,其代表的状态为S0
while 计算资源充足 do
扩展节点
对此节点代表的状态进行迭代扩展
为扩展出的节点代表的状态赋上迭代得到的值
return V0的最优的节点得到值
在这一整个过程中最初始的节点选取时常有着重要意义,其涉及到探索-利用问题,比较常用的衡量节点重要性的方法有UCT等,我们此处暂不作解释。
总结
本章主要介绍了在强化学习中对learning和planning的结合,以及一些planning的方法。其中planning和learning与planning的结合在许多需要模型快速收敛的问题上可能会有奇效