计算几何

定义

struct Vec {
    double x, y;
    Vec(double x = 0, double y = 0) : x(x), y(y) {}
    Vec operator + (const Vec & a) const { return Vec(x + a.x, y + a.y); }
    Vec operator - (const Vec & a) const { return Vec(x - a.x, y - a.y); }
    Vec operator * (const double a) const { return Vec(x * a, y * a); }
    double operator ^ (const Vec & a) const { return x * a.x + y * a.y; }
    double operator * (const Vec & a) const { return x * a.y - y * a.x; }
};

typedef Vec Pt;

struct Line {
    Pt p; Vec v;
};

点与直线的位置关系

bool online(Pt a, Line b) {
    return fabs((a - b.p) * b.v) < eps ? true : false;
}

两直线的位置关系

int check(Line a, Line b) {
    return fabs(a.v * b.v) < eps ? fabs(a.v * (b.p - a.p)) < eps ? 0 : 1 : 2;
}

求两直线的交点

（下图来自这里）

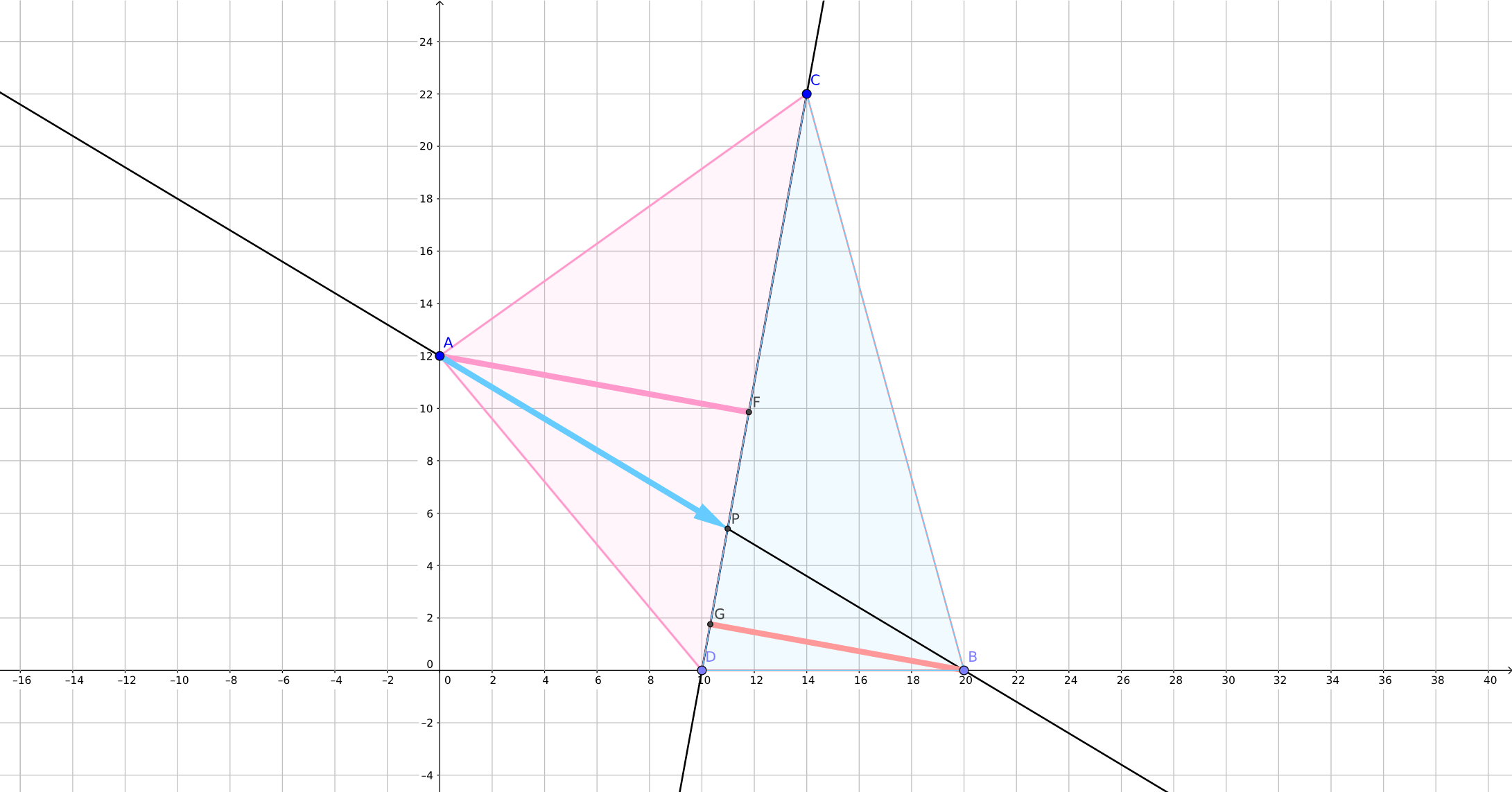
可推出 \(\frac{S_{四边形ABCD}}{S_{△ACD}} = \frac{AB}{AP}\)。

Pt cross(Line a, Line b) {
    return a.p + a.v * ((b.v * (a.p - b.p)) / (a.v * b.v));
}

旋转矩阵

将向量 \((x,y)\) 绕原点逆时针旋转 \(\theta\) 角：

\[\begin{bmatrix} x'\\ y' \end{bmatrix}= \begin{bmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} \]

即

\[x' = x\cos\theta - y\sin\theta\\ y' = x\sin\theta + y\cos\theta \]

一些性质

• 互相垂直的两向量的点积为 \(0\)。
• 在一条直线上的两向量的叉积为 \(0\)。
• 如果 \(\vec{a}\) 与 \(\vec{b}\) 的叉积为正，\(\vec{a}\) 与 \(\vec{c}\) 的叉积为负，则 \(\vec{b}\) 与 \(\vec{c}\) 分别在 \(\vec{a}\) 的两侧。
• 将向量的箭头向上，则左叉右为负，右叉左为正。

最小圆覆盖

#include <cmath>
#include <cstdio>
#include <algorithm>

const double eps = 1e-12;

struct Vec {
	double x, y;
	Vec(double x = 0, double y = 0) : x(x), y(y) {}
	Vec operator + (const Vec & a) const { return Vec(x + a.x, y + a.y); }
	Vec operator - (const Vec & a) const { return Vec(x - a.x, y - a.y); }
	Vec operator * (const double a) const { return Vec(x * a, y * a); }
	Vec operator / (const double a) const { return Vec(x / a, y / a); }
	double operator * (const Vec & a) const { return x * a.y - y * a.x; }
};
typedef Vec Pt;
struct Line { Pt p; Vec v; };
struct Cir { Pt p; double r; } c;
Pt p[100002]; int n;

double dis(Pt a, Pt b) {
	return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
}
Pt cross(Line a, Line b) {
	double s1 = (b.p - a.p) * (b.p + b.v - a.p), s2 = (b.p + b.v - a.p - a.v) * (b.p - a.p - a.v);
	return a.p + a.v * (s1 / (s1 + s2));
}
Vec rotate(Vec a) {
	return Vec(-a.y, a.x);
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i) scanf("%lf%lf", &p[i].x, &p[i].y);
	std::random_shuffle(p + 1, p + n + 1);
	c.p = p[1], c.r = 0;
	for (int i = 2; i <= n; ++i) {
		if (dis(c.p, p[i]) <= c.r + eps) continue;
		c.p = p[i], c.r = 0;
		for (int j = 1; j < i; ++j) {
			if (dis(c.p, p[j]) <= c.r + eps) continue;
			c.p = (p[i] + p[j]) / 2, c.r = dis(c.p, p[j]);
			for (int k = 1; k < j; ++k) {
				if (dis(c.p, p[k]) <= c.r + eps) continue;
				Line a, b;
				a.p = (p[i] + p[j]) / 2, b.p = (p[i] + p[k]) / 2;
				a.v = rotate(p[j] - p[i]), b.v = rotate(p[k] - p[i]);
				c.p = cross(a, b), c.r = dis(p[i], c.p);
			}
		}
	}
	printf("%.10lf\n%.10lf %.10lf", sqrt(c.r), c.p.x, c.p.y);
	return 0;
}

极角排序

此题为BZOJ 1132，题意是平面上有 \(n \le 3000\) 个点. 求出所有以这 \(n\) 个点为顶点的三角形的面积和。

利用叉积的分配律，用前缀和计算。

注意一开始的时候要将所有点按照 \(y < a.y || (y == a.y && x < a.x);\) 进行排序，否则后面的计算中会出现负数。

#include <cstdio>
#include <algorithm>

typedef long long LL;

struct Vec {
	LL x, y;
	Vec(LL x = 0, LL y = 0) : x(x), y(y) {}
	Vec operator + (const Vec & a) const { return Vec(x + a.x, y + a.y); }
	Vec operator - (const Vec & a) const { return Vec(x - a.x, y - a.y); }
	double operator * (const Vec & a) const { return x * a.y - y * a.x; }
	bool operator < (const Vec & a) const { return y < a.y || (y == a.y && x < a.x); }
};
typedef Vec Pt; Pt p[3002]; Vec v[3002]; LL ans;
LL read() {
	LL x = 0, f = 1; char c = getchar();
	while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
	return x * f;
}
bool cmp(Vec a, Vec b) {
	double c = a * b;
	return c == 0 ? a.x > b.x : c > 0;
}
int main() {
	int n = read();
	for (int i = 1; i <= n; ++i) p[i].x = read(), p[i].y = read();
	std::sort(p + 1, p + n + 1);
	for (int i = 1; i <= n - 2; ++i) {
		for (int j = i + 1; j <= n; ++j) v[j] = p[j] - p[i];
		std::sort(v + i + 1, v + n + 1, cmp);
		for (int j = i + 2; j <= n; ++j) ans += v[i + 1] * v[j], v[i + 1] = v[i + 1] + v[j];
	}
	printf("%lld", ans >> 1), puts(ans & 1 ? ".5" : ".0");
	return 0;
}

计算多边形的面积

#include <cstdio>

struct Vec {
	double x, y;
	Vec(double x = 0, double y = 0) : x(x), y(y) {}
	Vec operator - (const Vec & a) const { return Vec(x - a.x, y - a.y); }
	double operator * (const Vec & a) const { return x * a.y - y * a.x; }
};
typedef Vec Pt; Pt p[102]; int n; double ans;

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i) scanf("%lf%lf", &p[i].x, &p[i].y);
	for (int i = 2; i < n; ++i) ans += (p[i] - p[1]) * (p[i + 1] - p[1]);
	if (ans < 0) ans = -ans;
	printf("%.0lf\n", ans / 2);
	return 0;
}

旋转卡壳

BZOJ 1069 最大土地面积

枚举对角线，然后求左右两侧的最大三角形面积。

#include <cstdio>
#include <algorithm>

const double eps = 1e-6;

struct Vec {
	double x, y;
	Vec(double x = 0, double y = 0) : x(x), y(y) {}
	Vec operator - (const Vec & a) const { return Vec(x - a.x, y - a.y); }
	double operator * (const Vec & a) const { return x * a.y - y * a.x; }
	bool operator < (const Vec & a) const { return y < a.y || (y == a.y && x < a.x); }
};
typedef Vec Pt; Pt p[2002], sta[2002]; int n, top; double ans;
bool cmp(Pt a, Pt b) {
	double c = (a - p[1]) * (b - p[1]);
	return -eps <= c && c <= eps ? a.x > b.x : c > eps;
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i) {
		scanf("%lf%lf", &p[i].x, &p[i].y);
		if (p[i] < p[1]) p[0] = p[1], p[1] = p[i], p[i] = p[0];
	}
	std::sort(p + 2, p + n + 1, cmp);
	sta[1] = p[1], sta[2] = p[2], top = 2;
	for (int i = 3; i <= n; ++i) {
		while (top > 1 && (p[i] - sta[top]) * (sta[top - 1] - sta[top]) <= eps) --top;
		sta[++top] = p[i];
	}
	while (top > 1 && (p[1] - sta[top]) * (sta[top - 1] - sta[top]) <= eps) --top;
	for (int i = 1; i <= top - 2; ++i) {
		int x = i + 1, y = i + 2 == top ? 1 : i + 3;
		for (int j = i + 2; j <= top; ++j) {
			while ((sta[x + 1] - sta[i]) * (sta[j] - sta[i]) > (sta[x] - sta[i]) * (sta[j] - sta[i])) if (++x > top) x = 1;
			while ((sta[j] - sta[i]) * (sta[y + 1] - sta[i]) > (sta[j] - sta[i]) * (sta[y] - sta[i])) if (++y > top) y = 1;
			ans = std::max(ans, (sta[x] - sta[i]) * (sta[j] - sta[i]) + (sta[j] - sta[i]) * (sta[y] - sta[i]));
		}
	}
	printf("%.3lf", ans / 2);
	return 0;
}

旋转卡壳还可以计算：

• 两凸边形的最远距离（线1卡住凸边形1的最低点，线2卡住凸边形2的最高点，然后同时逆时针旋转，最远距离一定是点与点）
• 两凸边形的最近距离（线1卡住凸边形1的最低点，线2卡住凸边形2的最高点，然后同时逆时针旋转，最近距离可能是点与点、点与边、边与边）
• 凸边形的最小面积外接矩形（利用性质：矩形的一条边一定与凸边形的一条边重合）
• 凸边形的最小周长外接矩形（利用性质：矩形的一条边一定与凸边形的一条边重合）