"""
二叉树的list实现
"""
def BinTree(data, left=None, right=None):
"""
二叉树
:param data: 根结点的元素
:param left: 左子树元素
:param right: 右子树元素
:return:
"""
return [data, left, right]
def is_empty_BinTree(btree):
return btree is None
def root(btree):
return btree[0]
def left(btree):
return btree[1]
def right(btree):
return btree[2]
def set_root(btree, data):
btree[0] = data
def set_left(btree, left):
btree[1] = left
def set_right(btree, right):
btree[2] = right
if __name__ == '__main__':
t1 = BinTree(2, BinTree(4), BinTree(8))
print(t1) # [2, [4, None, None], [8, None, None]]
二叉树的简单应用:表达式树:
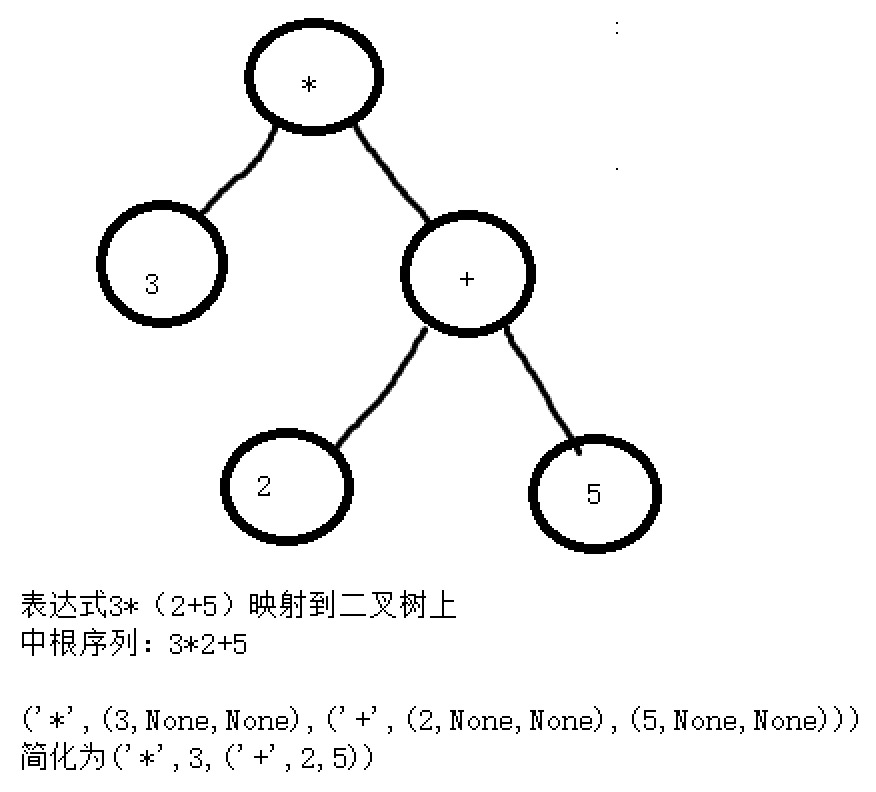
"""二叉树的简单应用:表达式树"""
# 表达式构造函数
def make_sum(a, b):
return ('+', a, b)
def make_prod(a, b):
return ('*', a, b)
def make_diff(a, b):
return ('-', a, b)
def make_div(a, b):
return ('/', a, b)
# 是否是基本表达式,也就是数或者变量
def is_basic_exp(a):
return not isinstance(a, tuple)
# 判断是否是数值
def is_number(x):
return isinstance(x, int) or isinstance(x, float) or isinstance(x, complex)
def eval_sum(a, b):
if is_number(a) and is_number(b):
return a + b
if is_number(a) and a == 0:
return b
if is_number(b) and b == 0:
return a
return make_sum(a, b)
def eval_div(a, b):
if is_number(a) and is_number(b):
return a / b
if is_number(a) and a == 0:
return 0
if is_number(b) and b == 1:
return a
if is_number(b) and b == 0:
raise ZeroDivisionError
return make_div(a, b)
def eval_diff(a, b):
if is_number(a) and is_number(b):
return a * b
if is_number(a) and a == 0:
return 0
if is_number(b) and b == 1:
return a
if is_number(a) and a == 1:
return b
if is_number(b) and b == 0:
return 0
return make_diff(a, b)
def eval_prod(a, b):
if is_number(a) and is_number(b):
return a - b
if is_number(a) and a == 0:
return -b
if is_number(b) and b == 0:
return a
return make_prod(a, b)
def eval_exp(e):
if is_basic_exp(e):
return e
# 递归处理子表达式
op, a, b = e[0], eval_exp(e[1]), eval_exp(e[2])
if op == '+':
return eval_sum(a, b)
elif op == '*':
return eval_diff(a, b)
elif op == '-':
return eval_prod(a, b)
elif op == '/':
return eval_div(a, b)
else:
raise ValueError("Unknown operator:", op)
el = make_prod(3, make_sum(2, 5))
print(el) # ('*', 3, ('+', 2, 5))
print(eval_exp(el)) # 21
el1 = make_prod(3, make_sum(-2, 5))
print(el1) # ('*', 3, ('+', -2, 5))
print(eval_exp(el1)) # 9




