05_3.递归与非递归、栈的应用--简单背包问题

阶乘函数的递归计算：

def fact(n):
    if n == 0:
        return 1
    else:
        return n * fact(n - 1)


if __name__ == '__main__':
    print(fact(3))  # 6

假定需要计算fact(3),其执行中将调用fact(2),进而调用fact(1)及fact(0)

 

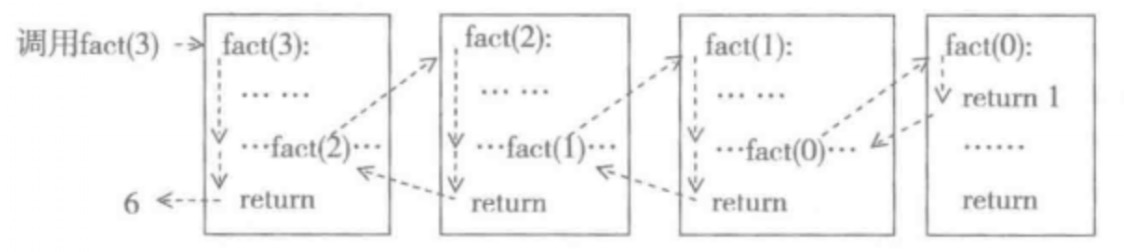
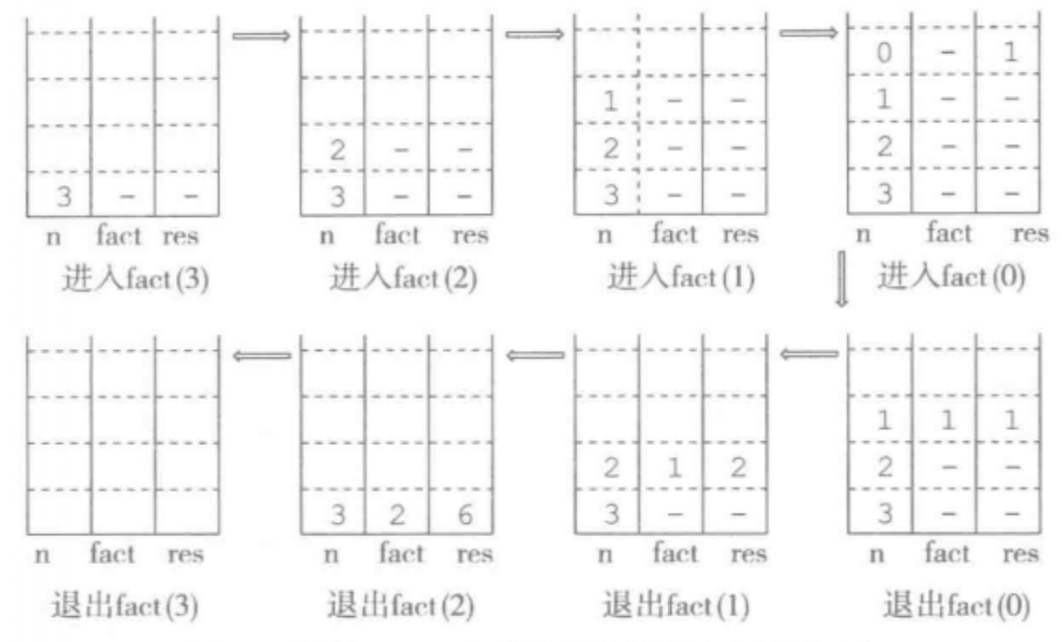
 计算过程中程序运行栈的变化情况，各小图中标着n一列的格子表示保存在栈的函数参数，fact表示调用fact的返回值，res表示本次函数调用的结果，显然res应=n*fact

 

 非递归阶乘：

def norec_fact(n):
    """n的阶乘"""
    res = 1
    st = SStack()
    while n > 0:
        st.push(n)
        n -= 1
    while not st.is_empty():
        res *= st.pop()
    return res

简单背包问题：

问题描述：一个背包可放入重量为weight的物品，现有n件物品的集合S，其中物品的重量分别为w0,w1,w2..wn-1，能否从中选出若干件物品，其重量之和正好等于weight，如果存在就说这一背包有解，否则就是无解。

def knap_rec(weight, wlist, n):
    """
    物品：w0，w1,w2,..,wn-1
    knap(weight,n)表示n件物品相对于重量weight的问题，在考虑它是否有解时，通过考虑一件物品的选或者不选，
    可以把原问题划分为两种情况：
    - 如果不选最后一件物品(即重量为wn-1)，那么knap(weight,n-1)的解也是knap(weight,n)的解
    - 如果选择最后一件物品，那么如果knap(weight-wn-1,n-1)有解，其解加上最后一件的物品就是knap(weight,n)的解，即前者有解后者也有解
    :param weight:总重量
    :param wlist:各物品重量表
    :param n:物品数目
    :return:
    """
    if weight == 0:
        return True
    if weight < 0 or (weight > 0 and n < 1):
        return False
    # if knap_rec(weight - wlist[n - 1], wlist, n - 1):
    #     print("Item" + str(n) + ":", wlist[n - 1])  # 递归最深的位置最先输出
    #     return True
    # else:
    #     return knap_rec(weight, wlist, n - 1)
    if knap_rec(weight - wlist[n - 1], wlist, n - 1):  # 表明选了这件物品
        print("Item" + str(n) + ":", wlist[n - 1])  # 递归最深的位置最先输出
        return True
    return knap_rec(weight, wlist, n - 1)  # 没有选择这件物品


if __name__ == '__main__':
    wlist = [2, 3, 3, 4, 5]
    print(knap_rec(10, wlist, len(wlist)))
# Item1: 2
# Item3: 3
# Item5: 5
# True