def naive_matching(t, p):
"""
朴素的串匹配算法
从左到右逐个字符匹配，发现不匹配时，转去考虑目标串里的下一个位置是否与模式串匹配
:param t: 目标串
:param p: 模式串
:return:
"""
m, n = len(p), len(t)
i, j = 0, 0
while i < m and j < n:
if p[i] == t[j]:
i, j = i + 1, j + 1
else:
i, j = 0, j - i + 1
if i == m:
return j - i
return -1
def matching_kmp(t, p, pnext):
"""KMP串匹配
如果i = -1，或者当前字符匹配成功（即t[j] == P[i]），都令i++，j++，继续匹配下一个字符；
如果i != -1，且当前字符匹配失败（即t[j] != P[i]），则令 j 不变，i = next[i]
next[j]即为j所对应的next值,此举意味着失配时，模式串P相对于目标串t向右移动了i - next [i] 位。
:param t: 目标串
:param p: 模式串
:return:
"""
i, j = 0, 0
m, n = len(p), len(t)
while i < m and j < n: # i==m说明找到匹配
if i == -1 or p[i] == t[j]: # 遇到-1或字符相等，匹配下一对字符
i, j = i + 1, j + 1
else: # 从pnext取的p的下一字符位置
i = pnext[i]
if i == m: # 找到匹配，返回其开始下标
return j - i
return -1 # 无匹配，返回特殊值
def gen_pnext(p):
"""
生成针对p中各位置i的下一检查位置表
计算最长相等前后缀的长度--递归求法
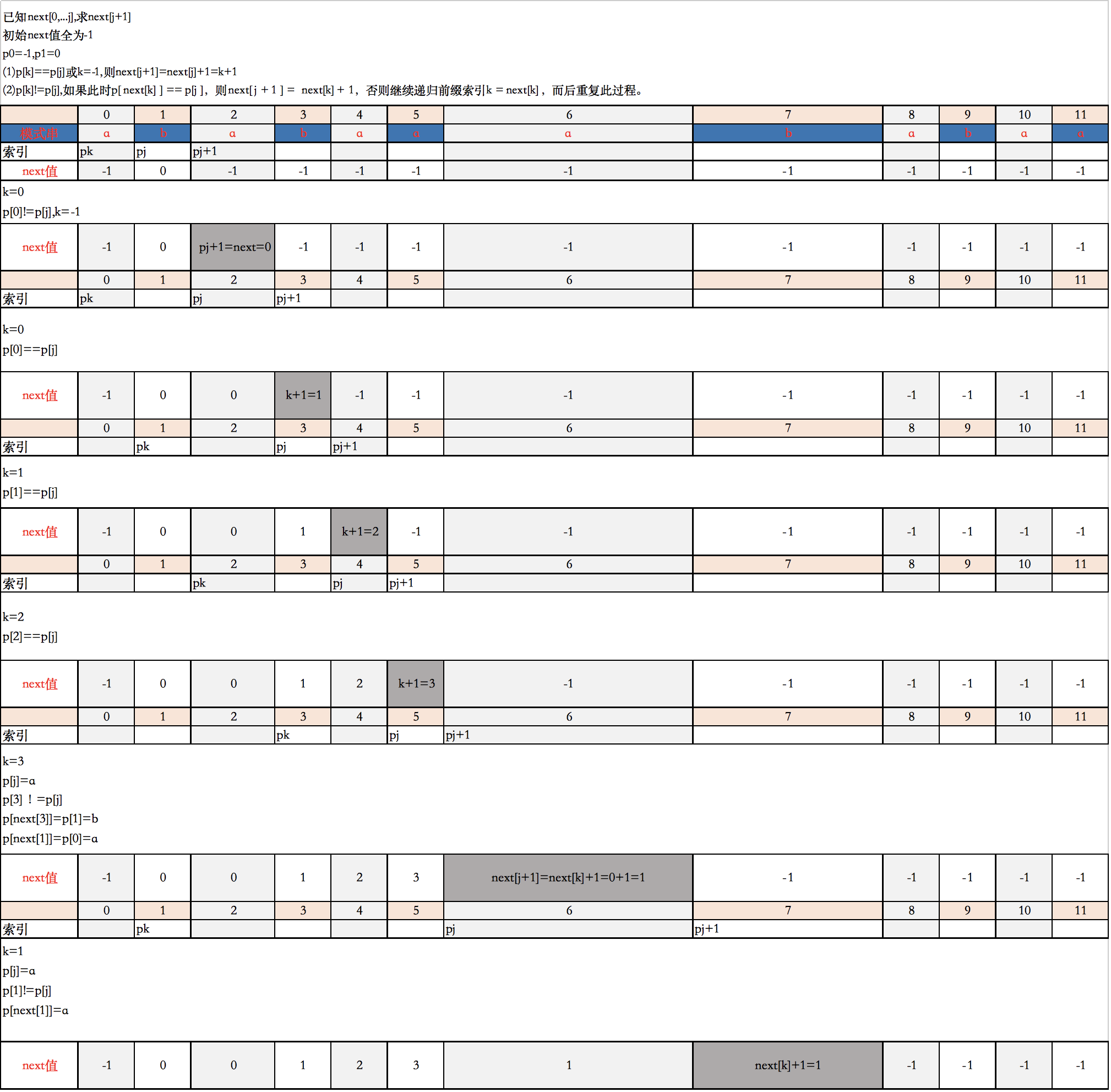
已知next [0, ..., i]，如何求出next [i + 1]呢？
对于P的前i+1个序列字符：
若p[i] == p[k]，则next[i + 1 ] = next [i] + 1 = k + 1；
若p[k ] ≠ p[i]，如果此时p[ next[k] ] == p[i]，则next[ i + 1 ] = next[k] + 1，
否则继续递归前缀索引k = next[k]，而后重复此过程
"""
i, k, m = 0, -1, len(p)
pnext = [-1] * m # 初始数组元素全为-1
while i < m - 1: # 生成下一个pnext元素值
if k == -1 or p[i] == p[k]:
i, k = i + 1, k + 1
pnext[i] = k # 设置pnext元素
else:
k = pnext[k] # 退到更短相同前缀
return pnext
if __name__ == '__main__':
print(naive_matching("ababc", "abc")) # 2
print(gen_pnext("abbcabcabbcaa")) # [-1, 0, 0, 0, 0, 1, 2, 0, 1, 2, 3, 4, 5]
print(gen_pnext("ababaaababaa")) # [-1, 0, 0, 1, 2, 3, 1, 1, 2, 3, 4, 5]
print(matching_kmp("ababc", "abc", gen_pnext("abc"))) # 2
"""参考博客：https://blog.csdn.net/dl962454/article/details/79910744"""
优化后的next求法：
def gen_pnext2(p):
"""
生成针对p中各位置i的下一检查位置表
优化：
p[i] ！= t[j]时，下次匹配必然时p[next[i]]与t[j]匹配，如果p[i]=p[next[i]]
必然p[next[i]]！=t[j]，匹配失败，需要再次递归，即令next[i] = next[ next[i] ]。
"""
i, k, m = 0, -1, len(p)
pnext = [-1] * m # 初始数组元素全为-1
while i < m - 1: # 生成下一个pnext元素值
# p[k]表示前缀，p[i]表示后缀
if k == -1 or p[i] == p[k]:
i, k = i + 1, k + 1
if p[i] == p[k]:
# 因为不能出现p[i] = p[ next[i]]，所以当出现时需要继续递归，k = next[k] = next[next[k]]
pnext[i] = pnext[k]
else:
pnext[i] = k
else:
k = pnext[k] # 退到更短相同前缀
return pnext
