08.前缀(波兰表达式)、中缀、后缀表达式(逆波兰表达式)

 

 

 前缀表达式的求值：

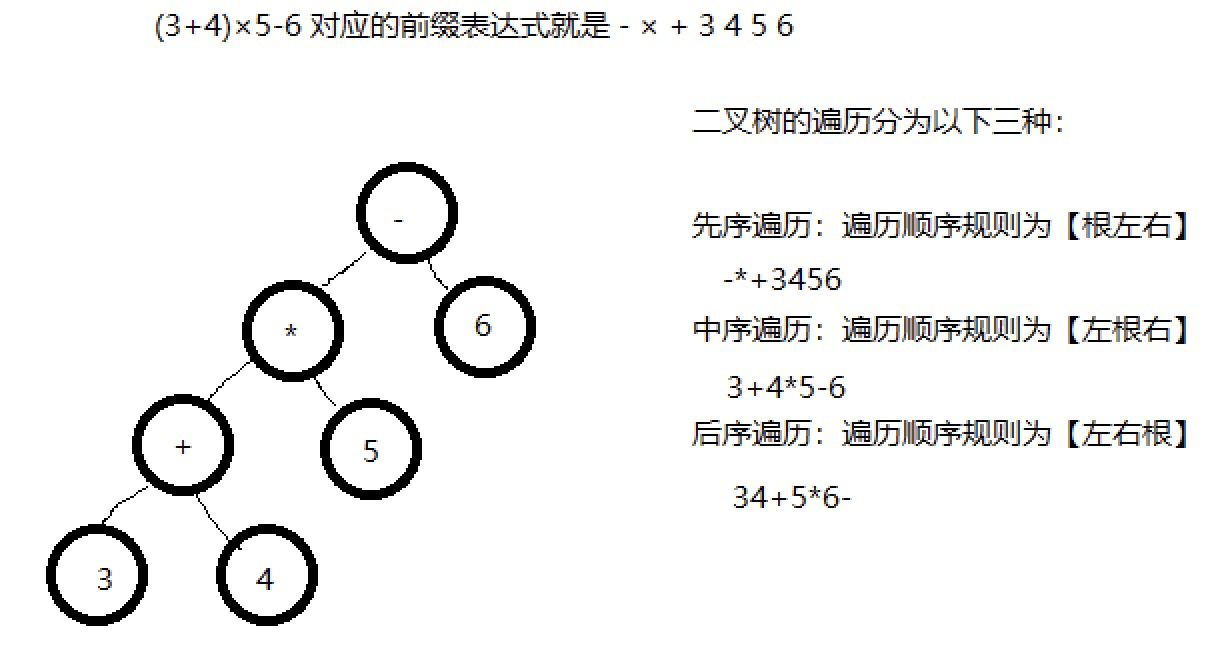
例如: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6 , 针对前缀表达式求值步骤如下:

- 从右至左扫描，将6、5、4、3压入堆栈

- 遇到+运算符，因此弹出3和4（3为栈顶元素，4为次顶元素），计算出3+4的值，得7，再将7入栈

- 接下来是×运算符，因此弹出7和5，计算出7×5=35，将35入栈

- 最后是-运算符，计算出35-6的值，即29，由此得出最终结果

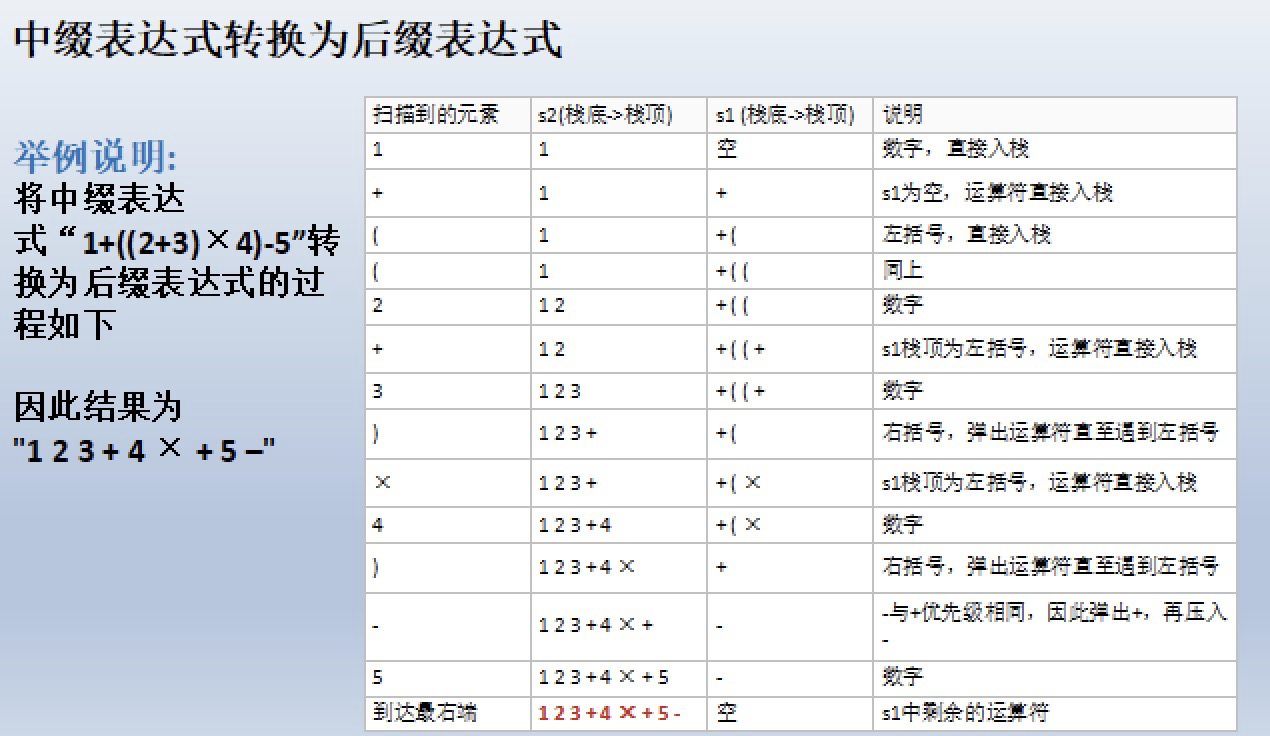
将中缀表达式转成后缀表达式:

(1)初始化两个栈：运算符栈s1和储存中间结果的栈s2；
(2)从左至右扫描中缀表达式；
(3)遇到操作数时，将其压s2；
(4)遇到运算符时，比较其与s1栈顶运算符的优先级：
    1.如果s1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
    2.若优先级比栈顶运算符的高，也将运算符压入s1,否则将s1栈顶的运算符弹出并压入到s2中，再次转到(4-1)与s1中新的栈顶运算符相比较；
(5)遇到括号时：
    1.如果是左括号“(”，则直接压入s1
    2.如果是右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
(6)重复步骤2至5，直到表达式的最右边
(7)将s1中剩余的运算符依次弹出并压入s2
(8)依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

import java.math.BigDecimal;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
import java.util.regex.Pattern;

/**
 * 逆波兰整数计算器
 */
public class PolandNotation {
    public static boolean isNumber(String s){
        Pattern pattern = Pattern.compile("^[-+]?[.\\d]+$");
        return pattern.matcher(s).matches();
    }
    //中缀表达式转化为list
    public static List<String> toInfixList(String s){
        if (s==null) throw new RuntimeException("空表达式");
        if (String.valueOf(s.charAt(0)).equals(")")) throw new RuntimeException("错误的表达式");
        //\\s+匹配任何空白字符，包括空格、制表符、换页符等，等价[\f\n\r\t\v]
        s = s.replaceAll("\\s+","");
        System.out.println(s);
        List<String> list = new ArrayList<>();
        int i = 0;
        char c;
        String str = "";
        do {
            c = s.charAt(i);
            //不是数字并且不是.
            if (String.valueOf(c).matches("[\\D]")&&!String.valueOf(c).equals(".")){
                if (i==0&&(!String.valueOf(c).equals("("))){//第一个字符不是(拼接到str
                    str += c;
                }else if (i!=0&&String.valueOf(c).equals("-")&&String.valueOf(s.charAt(i-1)).equals("(")){//非第一个字符，根据前一个是否是(判断是负号还上减号
                    str += c;
                }else {
                    list.add(String.valueOf(c));
                }
                i++;
            }else {
                while (i<s.length()&&String.valueOf(c=s.charAt(i)).matches("[\\d.]")){//是符号或是小数点
                    str += c;
                    i++;
                }
                int a = str.indexOf(".");
                if (a!=-1){
                    if (str.indexOf(".",a+1)!=-1) throw new RuntimeException("数字中保含多个小数点");
                }
                if (!String.valueOf(str.charAt(0)).matches("[-\\d]")){
                    str = str.substring(1);
                }
                list.add(str);
                str = "";
            }
        }while (i<s.length());
        return list;
    }
    //中缀表达式列表改为后缀表达式列表
    public static List<String> parseSuffixList(List<String> list){
        Stack<String> s1 = new Stack<>();
        List<String> s2 = new Stack<>();
        for (String item:list) {
            if (isNumber(item)){
                s2.add(item);
            }else if (item.equals("(")){
                s1.push(item);
            }else if (item.equals(")")){//遇到)就将s1中的弹出加入s2，直到遇到s1的(
                while (!s1.peek().equals("(")){
                    s2.add(s1.pop());
                }
                s1.pop();//弹出s1的(
            }else { //遇到符号了，看s1栈顶运算符，s1的优先级不小于它，就弹出放入s2，再与s1栈顶运算符比较，否则将这个符号放入s1
                while (s1.size()!=0&&(getValue(s1.peek())>=getValue(item))){
                    s2.add(s1.pop());
                }
                s1.push(item);
            }
        }
        //将s1中剩下的运算符依次弹出到s2
        while (s1.size()!=0){
            s2.add(s1.pop());
        }
        return s2;
    }
    public static int getValue(String oper){
        if (oper.equals("*")||oper.equals("×")||oper.equals("/")){
            return 2;
        }else if (oper.equals("+")||oper.equals("-")){
            return 1;
        }else {
            return -1;
        }
    }
    public static String calculate(List<String> list){
        Stack<String> stack = new Stack<>();
        for (String item : list) {
            if (isNumber(item)){
                stack.push(item);
            }else {
                String s2 = stack.pop();
                String s1 = stack.pop();
                BigDecimal res = BigDecimal.ZERO;
                BigDecimal b2 = new BigDecimal(s2);
                BigDecimal b1 = new BigDecimal(s1);
                if (item.equals("+")){
                    res = b1.add(b2);
                }else if (item.equals("-")){
                    res = b1.subtract(b2);
                }else if (item.equals("*")||item.equals("×")){
                    res = b1.multiply(b2);
                }else if (item.equals("/")){
                    res = b1.divide(b2,BigDecimal.ROUND_HALF_UP);
                }else {
                    throw new RuntimeException("运算符错误");
                }
                stack.push(String.valueOf(res));
            }
        }
        return stack.pop();
    }
    public static void main(String[] args){
        List<String> strings = toInfixList("-1+((-30 .  1-   4)×5 /5+1)- 6");//[-1, +, (, (, -30.1, -, 4, ), ×, 5, /, 5, +, 1, ), -, 6]
        System.out.println("strings2.toString() = " + strings.toString());
        List<String> strings2 = parseSuffixList(strings);
        System.out.println("strings2.toString() = " + strings2.toString());//[-1, -30.1, 4, -, 5, ×, 5, /, 1, +, +, 6, -]
        String calculate = calculate(strings2);
        System.out.println(calculate);//-40.1
    }
}