人工智能实战2019BUAA 第二次作业 张有驰
| 项目 | 内容 |
|---|---|
| 这个作业属于哪个课程 | 人工智能实战2019 |
| 这个作业的要求在哪里 | 第二次作业 |
| 我的GitHub账户 | zycMonster |
| 我在这个课程的目标是 | 个人课程目标 |
| 这个作业在哪个具体方面帮助我实现目标 | 通过动手及编程计算变量的反向传播过程,我对反向传播、梯度下降、误差函数等概念有了一定的认识,但较为浅显,不理解和神经网络的关系,通过后续课程应该能有更为深刻的认识;巩固了一定的Python基础语法,不过仍需加强学习 |
| 作业正文 | | |
| 其他参考文献 | | |
计算流程图
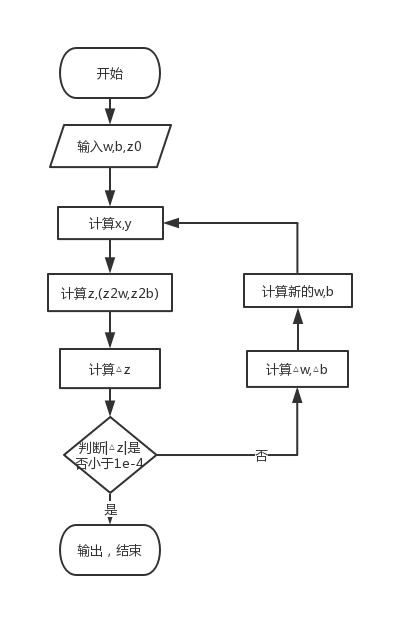
程序代码
def calculate_x(w,b): #定义计算关系式
return 2*w+3*b
def calculate_y(w,b):
return 2*b+1
def calculate_z(x,y):
return x*y
def cal_pd_z2w(x,y):
return 2*y
def cal_pd_z2b(x,y):
return 3*y+2*x
def cal_delta_z(z,z0):
return z-z0
def cal_delta_b(delta_z,z2b): #误差取一半分别给w,b
return (delta_z/2)/z2b
def cal_delta_w(delta_z,z2w):
return (delta_z/2)/z2w
def cal_new_b(b,delta_b):
return b-delta_b
def cal_new_w(w,delta_w):
return w-delta_w
if __name__=='__main__': #主函数
w=float(input('Please enter "w":')) #输入初值
b=float(input('Please enter "b":'))
z0=float(input('Please enter "z0":'))
x=calculate_x(w,b) #前向计算
y=calculate_y(w,b)
z=calculate_z(x,y)
z2w=cal_pd_z2w(x,y)
z2b=cal_pd_z2b(x,y)
delta_z=cal_delta_z(z,z0) #计算delta_z
print('w=%f,b=%f,z=%f,delta_z=%f'%(w,b,z,delta_z))
while delta_z>1e-4 or delta_z<-1e-4: #判断精度要求
delta_w=cal_delta_w(delta_z,z2w) #反向传播
delta_b=cal_delta_b(delta_z,z2b)
print('factor_w=%f,delta_w=%f,factor_b=%f,delta_b=%f'%(z2w,delta_w,z2b,delta_b))
w=cal_new_w(w,delta_w)
b=cal_new_b(b,delta_b)
x=calculate_x(w,b) #前向计算
y=calculate_y(w,b)
z=calculate_z(x,y)
#z2w=cal_pd_z2w(x,y) #重新计算贡献值
#z2b=cal_pd_z2b(x,y)
delta_z=cal_delta_z(z,z0)
print('w=%f,b=%f,z=%f,delta_z=%f'%(w,b,z,delta_z))
print("Done!")
print('Final w=%f'%w)
print('Final b=%f'%b)
误差结果
在每次迭代中都重新计算Δw和Δb的贡献值:
Please enter "w":3
Please enter "b":4
Please enter "z0":150
w=3.000000,b=4.000000,z=162.000000,delta_z=12.000000
factor_w=18.000000,delta_w=0.333333,factor_b=63.000000,delta_b=0.095238
w=2.666667,b=3.904762,z=150.181406,delta_z=0.181406
factor_w=17.619048,delta_w=0.005148,factor_b=60.523810,delta_b=0.001499
w=2.661519,b=3.903263,z=150.000044,delta_z=0.000044
Done!
Final w=2.661519
Final b=3.903263
没有在迭代中重新计算Δw和Δb的贡献值:
Please enter "w":3
Please enter "b":4
Please enter "z0":150
w=3.000000,b=4.000000,z=162.000000,delta_z=12.000000
factor_w=18.000000,delta_w=0.333333,factor_b=63.000000,delta_b=0.095238
w=2.666667,b=3.904762,z=150.181406,delta_z=0.181406
factor_w=18.000000,delta_w=0.005039,factor_b=63.000000,delta_b=0.001440
w=2.661628,b=3.903322,z=150.005526,delta_z=0.005526
factor_w=18.000000,delta_w=0.000154,factor_b=63.000000,delta_b=0.000044
w=2.661474,b=3.903278,z=150.000170,delta_z=0.000170
factor_w=18.000000,delta_w=0.000005,factor_b=63.000000,delta_b=0.000001
w=2.661469,b=3.903277,z=150.000005,delta_z=0.000005
Done!
Final w=2.661469
Final b=3.903277
分析
从以上两个结果对比中,可以看到三点:
- factor_w第一次是18,factor_b第一次是63,以后每次都会略微降低一些
- 第一个函数迭代了3次就结束了,而第二个函数迭代了5次,第一种方式效率高
- 最后得到的结果不一样,因为这个问题可以有多个解,两种方式都可以得到各自的正确解,但只有第一种方式满足梯度下降的概念
感想
这次作业花了不少时间在概念的理解上,以及变量的转换、迭代过程,最后没考虑Δz为负值的情况也出现了错误。总结如下:
- 在检查Δz时的值时,要考虑Δz为负的情况(可用绝对值),因为有可能是个负数
- 变量转换、迭代过程可画流程图,以便直观清晰的表示,弄清楚变量间的计算关系,区分变量和常量(如Δw和Δb的贡献值)



