关于 -128 ,+128,-0,+0,-1 的反码补码
一.反码的范围
反码表示法规定:正数的反码与其原码相同。负数的反码是对其原码逐位取反,但符号位除外。
在规定中,8位二进制码能表示的反码范围是-127~127。
此时(字长为8位), -128没有原码和反码(只有补码)。
那么,为什么规定字长8位时-128没有原码和反码呢?下面解释。
首先看-0,[-0]原码=1000 000,其中1是符号位,求反操作,算出[-0]反码=1111 1111,
再看-128,假如它有原码且[-128]原码=1000 000,假如让-128也有反码,求反操作,则[-128]反码=1111 1111,
你会发现,-128的反码和-0的反码相同,所以为了避免面混淆,有了-0的原码,便不能有-128的原码补码,这是8位比特位位数限制决定的。
二.原码 反码 补码的范围
前提:字长是8位二进制数。
原码 -127~127 (-128没有原码反码,原因看前面解释~)
反码 -127~127
补码 -128~127
对于n位二进制数:
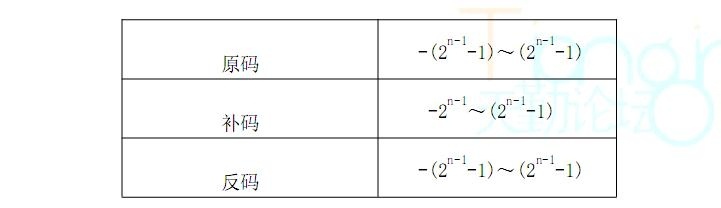
你会发现,补码比其它码多一位,这是为什么呢?问题出在0上。
[+0]原码=0000 0000, [-0]原码=1000 0000
[+0]反码=0000 0000, [-0]反码=1111 1111
[+0]补码=0000 0000, [-0]补码=0000 0000
你会发现,+0和-0的补码是一样的。即 0的补码只有一种表示。
这里解释一下[-0]补码是怎么得来的。
负数的补码就是反码整体加一。符号位上的进位舍弃。(所以,舍弃了符号位的补码的第一位是数值位,不是符号位,符号位舍弃了)
另外解释一下原码符号位和补码符号位的关系,补码的符号位不是保持原码的第一位不变,而是 符号位不变,[-0]反码的第一个1是符号位,尾数中的7个1是数值位,尾数加一后,数值位产生了进位,1111 1111+1=1 0000 0000(计算补码的过程中,并不是先保证第一位不变,而是保证符号位不变,保证补码规则是反码整体加一)。
所以,补码能表示的数的个数中,比原码反码少了一个,所以补码可以多表示一个真值为-128的数。
但是,多表示的这个数-128比较特殊,只有原码和补码,没有反码。
-128的补码是1000 0000。
三.-128的补码为什么是1000 0000
+128的原值在8位中是表达不出来的。
所以 256+(-128)的补码=128
所以 (-128)的补码=256-128
=128
数学上, 128=1000 0000
故规定-128的补码为 1000 0000
0000 0000 - 0111 1111 0 ~+127
1000 0000 用来干啥好呢?
原码 补码 值
0111 1111 0111 1111 +127
0111 1110 0111 1110 +126
... .. 补码不断-1...
0000 0000 0000 0000 0
1000 0001 1111 1111 -1
1000 0010 1111 1110 -2
1000 0011 1111 1101 -3
... .. 补码不断-1...
1111 1111 1000 0001 -127
无法表达 1000 0000 -128
这种定法和上面数学层面的表述是一致的。
将该负数取绝对值,再用二进制表示出这个绝对值 (不管符号位!)
对该二进制数进行取反加一操作就得到负数的补码了 (也就是求补操作!)
-128 绝对值是 128
128的二进制表示为:
1000 0000
取反
0111 1111
加1
1000 0000
这就是-128的补码
这种办法算出的结果符合“规定值”。
四.
1字节 = 8位,所以它能表示的最大数当然是8位都是1(既然2进制的数只能是0或1,如果是我们常见的10进制,那就8位都为9,这样说,你该懂了?)
1字节的二进制数中,最大的数:11111111。
双字节共16位。 1111111111111111。双字节数最大值为:
1 * 215 + 1 *214 + 1* 213 + 1 * 212 + 1 * 211 + 1 * 210 + …… + 1 * 22 + 1 * 21 + 1* 20 = 65535
负数在计算机中如何表示呢?
这一点,你可能听过两种不同的回答。
一 种是教科书,它会告诉你:计算机用“补码”表示负数。可是有关“补码”的概念一说就得一节课,这一些我们需要在第6章中用一章的篇幅讲2进制的一切。再 者,用“补码”表示负数,其实是一种公式,公式的作用在于告诉你,想得到问题的答案,应该如何计算。却并没有告诉你为什么用这个公式就可以得到答案! -----我就是被这个弄混淆的>_<
另 一种是一些程序员告诉你的:用二进制数的最高位表示符号,最高位是0,表示正数,最高位是1,表示负数。这种说法本身没错,可是如果没有下文,那么它就是 错的。至少它不能解释,为什么字符类型的-1用二进制表示是“1111 1111”(16进制为FF);而不是我们更能理解的“1000 0001”。(为什么说后者更好理解呢?因为既然说最高位是1时表示负数,那1000 0001不是正好是-1吗?-----re!当初偶就是这么想的,so一直在脑中打架,越打越混淆=,=)。
让我们从头说起。
2.1、你自已决定是否需要有正负。
就像我们必须决定某个量使用整数还是实数,使用多大的范围数一样,我们必须自已决定某个量是否需要正负。如果这个量不会有负值,那么我们可以定它为带正负的类型。
在计算机中,可以区分正负的类型,称为有符类型,无正负的类型(只有正值),称为无符类型。
数值类型分为整型或实型,其中整型又分为无符类型或有符类型,而实型则只有有符类型。
字符类型也分为有符和无符类型。
比如有两个量,年龄和库存,我们可以定前者为无符的字符类型,后者定为有符的整数类型。
3、无符号数和有符号数的范围区别。
同样是一个字节,无符号数的最大值是255,而有符号数的最大值是127。原因是有符号数中的最高位被挪去表示符号了。并且,我们知道,最高位的权值也是最高的(对于1字节数来说是2的7次方=128),所以仅仅少于一位,最大值一下子减半。
不过,有符号数的长处是它可以表示负数。因此,虽然它的在最大值缩水了,却在负值的方向出现了伸展。我们仍一个字节的数值对比:
无符号数: 0 ----------------- 255
有符号数: -128 ----- 0 ----- 127
同样是一个字节,无符号的最小值是 0 ,而有符号数的最小值是-128。所以二者能表达的不同的数值的个数都一样是256个。只不过前者表达的是0到255这256个数,后者表达的是-128到+127这256个数。
一个有符号的数据类型的最小值是如何计算出来的呢?
有符号的数据类型的最大值的计算方法完全和无符号一样,只不过它少了一个最高位(见第3点)。但在负值范围内,数值的计算方法不能直接使用1* 26 + 1* 25 的公式进行转换。在计算机中,负数除为最高位为1以外,还采用补码形式进行表达。所以在计算其值前,需要对补码进行还原。这里,先直观地看一眼补码的形式:
以我们原有的数学经验,在10进制中:1 表示正1,而加上负号:-1 表示和1相对的负值。
那么,我们会很容易认为在2进制中(1个字节): 0000 0001 表示正1,则高位为1后:1000 0001应该表示-1。
然而,事实上计算机中的规定有些相反,请看下表:
| 二进制值(1字节) | 十进制值 |
| 1000 0000红色的1代表负数蓝色的是补码(补码=反码+1) | -128 |
| 1000 0001蓝色部分代表多大的值?:将补码还原为原码 | -127想化成负数?:先减去1再按位取反 |
| 1000 0010还原方法:补码-1再取反 | -126 |
| 1000 0011 | -125 |
| ... | ... |
| 1111 1110 | -2 |
| 1111 1111 | -1 |
首先我们看到,从-1到-128,其二进制的最高位都是1(表中标为红色),正如我们前面的学。
然后我们有些奇怪地发现,1000 0000 并没有拿来表示 -0;而1000 0001也不是拿来直观地表示-1。事实上,-1 用1111 1111来表示。
怎么理解这个问题呢?先得问一句是-1大还是-128大?
当 然是 -1 大。-1是最大的负整数。以此对应,计算机中无论是字符类型,或者是整数类型,也无论这个整数是几个字节。它都用全1来表示 -1。比如一个字节的数值中:1111 1111表示-1,那么,1111 1111 - 1 是什么呢?和现实中的计算结果完全一致。1111 1111 - 1 = 1111 1110,而1111 1110就是-2。这样一直减下去,当减到只剩最高位用于表示符号的1以外,其它低位全为0时,就是最小的负值了,在一字节中,最小的负值是1000 0000,也就是-128。
--------小米批注:就是这部分蓝色的文字,让我终于能记清楚-1的编码方式了,汗=。=
我们以-1为例,来看看不同字节数的整数中,如何表达-1这个数:
| 字节数 | 二进制值 | 十进制值 |
| 单字节数 | 1111 1111红色表示负数蓝色部分的补码为值1 | -1 |
| 负数:原码就是原来的表示方法、反码是除符号位(最高位)外取反、补码=反码+1双字节数 | 1111 1111 1111 1111 | -1 |
| 四字节数 | 1111 1111 1111 1111 1111 1111 1111 1111 | -1 |
可 能有同学这时会混了:为什么 1111 1111 有时表示255,有时又表示-1?
所以我再强调一下本节前面所说的第2点:你自已决定一个数是有符号还是无符号的。写程序时,指定一个量是有符号的,那么 当这个量的二进制各位上都是1时,它表示的数就是-1;相反,如果事先声明这个量是无符号的,此时它表示的就是该量允许的最大值,对于一个字节的数来说, 最大值就是255。
ok 摘抄暂告段落,其实原文对于c的一些基础数据类型知识介绍的非常详细,8过太长了,摘到我需要的内容后就没全帖过来,如果有需要学习的同学,建议参见原文:)
在计算机内部,所有信息都是用二进制数串的形式表示的。整数通常都有正负之分,计算机中的整数分为无符号的和带符号的。无符号的整数用来表示0和正整数, 带符号的证书可以表示所有的整数。由于计算机中符号和数字一样,都必须用二进制数串来表示,因此,正负号也必须用0、1来表示。通常我们用最高的有效位来 表示数的符号(当用8位来表示一个整数时,第8位即为最高有效位,当用16位来表示一个整数时,第16位即为最高有效位。)0表示正号、1表示负号,这种 正负号数字化的机内表示形式就称为“机器数”,而相应的机器外部用正负号表示的数称为“真值”。将一个真值表示成二进制字串的机器数的过程就称为编码。
无符号数没有原码、反码和补码一说。只有带符号数才存在不同的编码方式。
带符号整数有原码、反码、补码等几种编码方式。原码即直接将真值转换为其相应的二进制形式,而反码和补码是对原码进行某种转换编码方式。正整数的原 码、反码和补码都一样,负数的反码是对原码的除符号位外的其他位进行取反后的结果(取反即如果该位为0则变为1,而该位为1则变为0的操作)。而补码是先 求原码的反码,然后在反码的末尾位加1 后得到的结果,即补码是反码+1。IBM-PC中带符号整数都采用补码形式表示。(注意,只是带符号的整数采用补码存储表示的,浮点数另有其存储方式。)
采用补码的原因或好处如下。
采用补码运算具有如下两个特征:
1)因为使用补码可以将符号位和其他位统一处理,同时,减法也可以按加法来处理,即如果是补码表示的数,不管是加减法都直接用加法运算即可实现。
2)两个用补码表示的数相加时,如果最高位(符号位)有进位,则进位被舍弃。
这样的运算有两个好处:
1)使符号位能与有效值部分一起参加运算,从而简化运算规则。从而可以简化运算器的结构,提高运算速度;(减法运算可以用加法运算表示出来。)
2)加法运算比减法运算更易于实现。使减法运算转换为加法运算,进一步简化运算器线路设计。
下面深入分析上面所陈述的采用补码的原因(目的)。
用带符号位的原码进行乘除运算时结果正确,而在加减运算的时候就出现了问题,如下:假设字长为8bits
1 D- 1 D = 1 D + ( -1 )D = ( 0 )D
(00000001)原 + (10000001)原 = (10000010)原 = ( -2 ) 显然不正确.。
因为在两个整数的加法运算中是没有问题的,于是就发现问题出现在带符号位的负数身上,对除符号位外的其余各位逐位取反就产生了反码。反码的取值空间和原码相同且一一对应。下面是反码的减法运算:
1 D- 1 D = 1 D + ( -1 )D = ( 0 )D
(00000001) 反+ (11111110)反 = (11111111)反 = ( -0 ) 有问题。
1 D - 2 D= 1 D+ ( -2 )D = ( -1 )D
(00000001) 反+ (11111101)反 = (11111110)反 = ( -1 ) 正确
问题出现在(+0)和(-0)上,在人们的计算概念中零是没有正负之分的。
于是就引入了补码概念。负数的补码就是对反码加一,而正数不变,正数的原码反码补码是一样的。在补码中用(-128)代替了(-0),所以补码的表示范围为:
(-128~0~127)共256个。
采用补码表示还有另外一个原因,那就是为了防止0的机器数有两个编码。原码和反码表示的0有两种形式+0和-0,而我们知道,+0和-0是相同的。这 样,8位的原码和反码表示的整数的范围就是-127~+127(11111111~01111111),而采用补码表示的时候,00000000是+0, 即0;10000000不再是-0,而是-128,这样,补码表示的数的范围就是-128~+127了,不但增加了一个数得表示范围,而且还保证了0编码 的唯一性。
接下来的问题是,如何能将减法运算转换成加法运算呢?
我们已经知道,原码表示简单直观,与真值转换容易。但如果用原码表示,其符号位不能参加运算。在计算机中用原码实现算术运算时,要取绝对值参加运算,符号位单独处理,这对乘除运算是很容易实现的,但对加减运算是非常不方便的,如两个异号数相加,实际是要做减法,而两个异号数相减,实际是要做加法。在做减法时,还要判断操作数绝对值的大小,这些都会使运算器的设计变得很复杂。而补码这种编码方式实际上正是针对上述问题的。通过用补码进行表示,就可以把减法运算化为加法运算。
在日常生活中,有许多化减为加的例子。例如,时钟是逢12进位,12点也可看作0点。当将时针从10点调整到5点时有以下两种方法:
一种方法是时针逆时针方向拨5格,相当于做减法:
10-5=5
另一种方法是时针顺时针方向拨7格,相当于做加法:
10+7=12+5=5 (MOD 12)
这是由于时钟以12 为模,在这个前提下,当和超过12时,可将12舍去。于是,减5相当于加7。同理,减4可表示成加8,减3可表示成加9,…。
在数学中,用“同余”概念描述上述关系,即两整数A、B用同一个正整数M (M称为模)去除而余数相等,则称A、B对M同余,记作:
A=B (MOD M)
具有同余关系的两个数为互补关系,其中一个称为另一个的补码。当M=12时,-5和+7,-4和+8,-3和+9就是同余的,它们互为补码。
从同余的概念和上述时钟的例子,不难得出结论:对于某一确定的模,用某数减去小于模的另一个数,总可以用加上“模减去该数绝对值的差”来代替。因此,在有模运算中,减法就可以化作加法来做。
可以看出,补码的加法运算所依据的基本关系为:
[x]补+ [y]补= [x+y]补
补码减法所依据的基本关系式:
[x-y]补 =[x+(-y)]补= [x]补+ [-y]补
至于加法运算为什么比减法运算易于实现以及CPU如何实现各种算术运算等问题,则需要通过对数字电路的学习来理解CPU的运算器的硬件实现问题的相关内容了。
五.
1.一个二进制数的补码的补码就是原码!!!
比如:真值-3,原码1000 0011,补码1111 1101,
原码1111 1101,补码1000 0011。
也可以从补码的数学含义理解。
2.几个特殊的补码记忆:(一般是8位,不是8位和8的倍数位的,在实际应用中没有意义,所以一般都是变换成成8位的二进制数。因为实际应用中,一般都是补码表示,所以着重记忆补码)
0的补码是0000 0000
-1的补码是1111 1111 -1的原码是1000 0001
-128的补码是1000 0000
+1的补码是其原码。
+1~+127的补码都是原码。补码逐渐加一。
-1~-127的补码都是其反码加一。补码逐渐加一。
虽然补码的原码是多少 不够直观,但是补码反映出的负数的大小是直观的,补码大小顺序和真值保持一致。
负数真值中,-1最大,-128最小,
负数补码中,-1补码是1111 1111,...,-127补码是1000 0001,-128补码是1000 0000,
在负数的补码中,直观上可以看出,-1的补码是最大的:1111 1111, -128的补码是最小的:1000 0000。
3.
80H的补码是多少?
因为有补码,所以是有符号数。80H即原码1000 0000,即真值-0,所以80H的补码是0000 0000。
六.+128
8位二进制数时,表示不下+128,16位二进制数时可以表示。因为+128=0001 0000 0000
8位二进制数的原码范围是-127~-0,+0,~127,反码是-127~-0,+0~+127,补码范围是-128~0~+127。范围都是256个整数。
不包括+128。-128也只在补码表示中有。-128的原码和反码在8位二进制数时也都没有,在16位及以上可以表示。
七.探究求补码的最好的方法
-0的原码是 1000 0000,反码 1111 1111, 补码 0000 0000,可以反码加一,可以对-1求补操作。
-3的原码是 1000 0011,反码 1111 1100 ,补码 1111 1101,可以反码加一,可以对-3求补操作。
-128原码是 没有 反码 没有 补码 1000 0000 可以对-128求补操作。
由上面三个例子可以看出,求补码的最快捷的方法,第一位不变什么的 只适用于不是-1 -128的大部分数!
最统一的方法,应该是:
有反码的,反码加一(其中,符号位有进位的 舍弃符号位 只保留数值位。比如-0的补码。更重要的是-0的补码 是规定),或者求补操作。
没有反码的,求补操作。比如-128。
所以说,求补操作,才是对-128~+127唯一全部使用的求补码的方法。
这样也就解释了,为什么所有补码都可以用补码减法运算了,因为求补操作对所有真值都适用。
求补操作:就是求(负数的)补码
求补操作:不管符号位(不是符号位保持不变!也不是第一位保持不变!就是只用负数的绝对值,根本没用到符号位),取负数(真值)的绝对值(即将负数的符号位变为0),对绝对值按位取反(可以认为绝对值是无符号数),然后加一。就得到了负数的补码。
求补操作对于求-0,-128也都适用。
例子:求3CH-90H。分为有符号数和无符号数时。
0011 1100
- 1001 0000
----------------------
3CH 和90H 不是真值!只有十进制是真值,而 十六进制或者八进制 都是为了书写二进制码方便。所以才说3CH可能是无符号数 也可能是有符号数!
3CH 和90H 就是两个二进制码!这两个二进制码可能是无符号数或者有符号数!
二进制码(二进制数)分为有符号数和无符号数。
有符号数时,X-Y=X+(-Y)补,所以,求-90H的补码,即求-1001 0000的补码。即对-1001 0000求补操作!不是对1001 0000求补操作!90H是绝对值,-90H是真值,1001 0000是绝对值的二进制码。
--------------------------
这里解释一下题目要求的意思:
(1)机器只认识二进制。十六进制和八进制是为了人书写简洁而设立的。
(2)有符号数和无符号数说的都是二进制数(二进制码)。
3CH的二进制码是唯一的,但是当它是有符号数时和是无符号数时 的真值显然是不同的。




