动手实现一个跳表
前言
本文主要介绍跳表的特点,以及如何自己实现一个跳表。
跳表(SkipList)
跳表是一个典型的空间换时间模型,底层数据结构是一个有序的单链表,通过构建多层索引,实现了二分查找方式来查询数据。多层索引不仅提高了查询效率,同时也使得插入和删除的时间复杂度为O(logn)。此外,多层索引的空间复杂度为O(n)。
跳表是一个随机化的动态数据结构,它引入了多层索引,所以在运行期间需要维护索引和原始数据的平衡性。不像红黑树、AVL树通过左右旋的方式保持左右子树的平衡,跳表通过随机函数来随机需要构建的索引层数,从而维护平衡性。
跳表在性能上和红黑树、AVL树不相上下,但是跳表的实现比较简单,目前在Redis、LevelDB上都有使用。
以上介绍了跳表的特点,下面贴上具体代码实现:
package main.java.skiplist;
import java.util.Random;
/**
* 传统跳表
* 1. 元素不能重复
* 2. 索引层数随机
*/
public class SkipList {
// 随机工具,用于随机索引层数
private final Random random;
public final int MAX_LEVEL = 16;
// 当前层数
public int level;
public SkipNode head;
public SkipList() {
random = new Random();
head = new SkipNode(Integer.MIN_VALUE, MAX_LEVEL);
level = 1;
}
/**
* 返回随机建造索引层数
* @return [1, MAX_LEVEL]
*/
private int randomLevel() {
int n = 1;
for (int i = 1; i < MAX_LEVEL; i++) {
if (random.nextInt(2) == 1)
n++;
}
return n;
}
/**
* 根据 val 查询结点
* @param val 结点值
* @return 如果值不存在,返回 null;否则返回查询的结点
*/
public SkipNode find(int val) {
SkipNode p = head;
for (int i=level-1; i>=0; i--) {
while (p.next[i] != null && p.next[i].value < val) {
p = p.next[i];
}
}
return p.next[0] != null && p.next[0].value == val ? p.next[0] : null;
}
/**
* 根据 val 删除节点
* @param val 结点值
* @return 如果值不存在,返回 null;否则返回删除的结点
*/
public SkipNode delete(int val) {
SkipNode[] prev = new SkipNode[MAX_LEVEL];
SkipNode p = head;
for (int i=level-1; i>=0; i--) {
while (p.next[i] != null && p.next[i].value < val) {
p = p.next[i];
}
prev[i] = p;
}
if (p.next[0] != null && p.next[0].value == val) {
SkipNode res = p.next[0];
for (int i = 0; i < res.level; i++) {
prev[i].next[i] = prev[i].next[i].next[i];
}
return res;
}
return null;
}
/**
* 插入节点
* @param val 结点值
*/
public void insert(int val) {
int newLevel = randomLevel();
SkipNode newNode = new SkipNode(val, newLevel);
SkipNode[] prev = new SkipNode[newLevel];
SkipNode p = head;
for (int i=newLevel-1; i>=0; i--) {
while (p.next[i] != null && p.next[i].value < val) {
p = p.next[i];
}
prev[i] = p;
}
for (int i=0; i<newLevel; i++) {
newNode.next[i] = prev[i].next[i];
prev[i].next[i] = newNode;
}
if (newLevel > level)
level = newLevel;
}
public void show() {
StringBuffer sb = new StringBuffer();
int col = 0;
SkipNode p = head.next[0];
while (p != null) {
p.setSpan(col);
col++;
p = p.next[0];
}
SkipNode[] arr = head.next;
for (int i=level-1; i>=0; i--) {
sb.append(String.format("第%2d层: ", i));
p = arr[i];
for (int j = 0; j < col; j++) {
if (p != null && p.span == j) {
sb.append(p.value);
p = p.next[i];
}else {
sb.append(" ");
}
if (j != col-1)
sb.append(" -> ");
}
sb.append("\n");
}
System.out.println(sb.toString());
}
public static final class SkipNode {
int level;
int value;
int span; // 辅助打印
SkipNode[] next;
public SkipNode(int v, int level) {
value = v;
this.level = level;
next = new SkipNode[level];
}
@Override
public String toString() {
return "SkipNode{" +
"level=" + level +
", value=" + value +
", span=" + span +
'}';
}
public void setSpan(int span) {
this.span = span;
}
}
}
效果截图
原始数据:
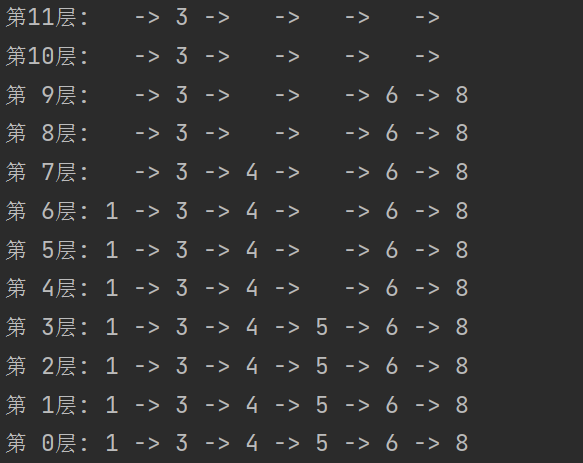
查询和删除:
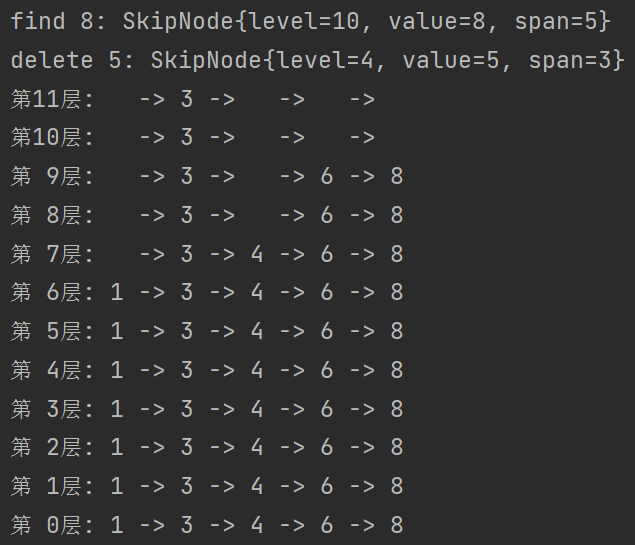
参考
- [1] 【数据结构与算法】之跳表


