manacher马拉车算法

Manacher算法讲解

总有人喜欢搞事情，出字符串的题，直接卡掉了我的40分

I.适用范围

manacher算法解决的是字符串最长回文子串长度的问题。

关键词：最长 回文 子串

II.算法

1.纯暴力怎么写？

枚举每个字串（n^2）

判断是否回文（n）

综上，时间为n^3。

能解决n < 300的数据

2.优化的暴力

枚举点（n）

从点开始向两边逐个扩展，统计回文串的长度（上界n，但随机情况下很小）

综上，时间为n^2。

在随机数据下，实际表现能达到大概(n^2 / logn)的速度。

能解决5000左右的数据。

 

我们定义回文串的半径为回文串的回文中心到回文串的一端中间有多少个字符（不包含中心，包含端点）

比如回文串floatiyyitaolf的半径就是7，而vanav的半径是2。

对于长度是奇数和偶数的串要分类讨论。

给个示意的代码：

for(int i = 1;i <= n;i++) {
    回文串的半径 k = 0;
    while(s[i-k] == s[i+k]) k++;
    ans = max(k*2+1,ans);
}

 

3.更优秀的算法——manacher

manacher可以看作是对上面那个n^2算法的进一步优化。

在枚举点统计回文串的过程中，我们其实是计算出了一些有用的信息，这些信息可以被后面的点使用，而无需重复计算（跟kmp有点像？）。

具体来说，我们从左向右枚举点，每次记录一下以这个点为中心的最长回文子串的半径（以i为中心的最长半径记为p[i]）。

我们要试着利用回文的性质，因为子串是回文的，所以对于任意一个点x，有s[x - k] = s[x + k]  (k<= p[x])。这条性质可以省去重复比较字符的过程。

manacher的算法流程：

记录现在最大的(p[i] + i)为maxright，maxright对应的i为pos。

枚举下一个位置i时，i与maxright和pos有下面三种情况：

 

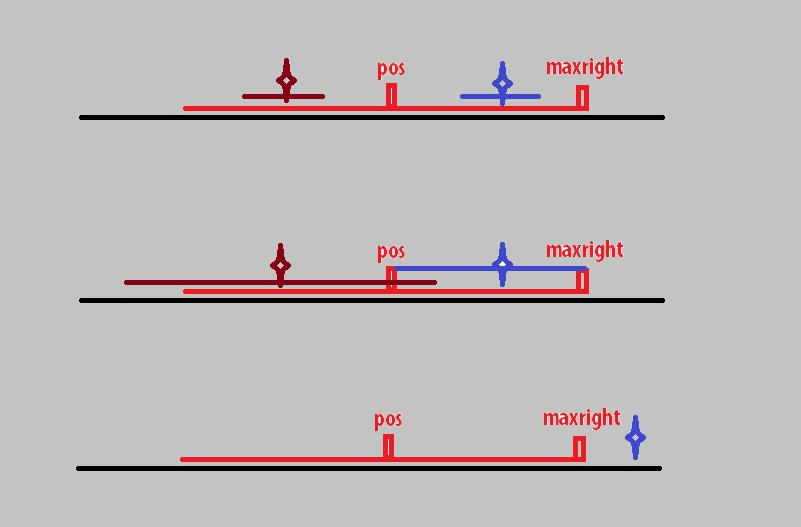
蓝星星代表i点，褐色星星代表i点关于pos的对称点j。

情况1：

p[j]较小，被p[pos]完全包含，那么由于pos的两边是对称的，那么蓝色区间一定是回文的，我们只要在蓝色区间的基础上再找更大的回文区间就可以了。

情况2：

p[j]较大，但我们只能保证红色区间是回文的，所以情况二中的蓝色区间是回文的，求更大的蓝色回文区间仍需要逐个扩展。

情况3：

此时i已经超出了maxright，不在红色范围，内此时只能逐个扩展。

每次扩展完毕要更新pos和maxright。

 

manacher还处理了一个问题：字串长度是奇数偶数要分类讨论。

具体方法是在每个字符的前后都保证有一个不在题目给的串里出现的字符，强行转化成奇数个字符。

AAADJ —> #A#A#A#D#J#

Code

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

const int MAXN = 11000000 + 5;

int n,ans;
int maxright,pos;
int p[MAXN<<1];
char t[MAXN<<1],s[MAXN<<1];

inline int _max(int x,int y) {
    return x > y ? x : y;
}

inline int _min(int x,int y) {
    return x < y ? x : y;
}

int main() {
    scanf("%s",t+1);
    n = strlen(t+1);
    s[0] = '@';
    for(register int i = 1;i <= n;i++) {
        s[i+i-1] = '#';
        s[i+i] = t[i];
    }
    n = n+n+1; s[n] = '#';
    for(register int i = 1;i <= n;i++) {
        if(i < maxright) p[i] = _min(p[pos+pos-i],maxright-i);
        while(s[i-p[i]] == s[i+p[i]]) p[i]++;
        ans = _max(ans,p[i]);
        if(i+p[i] > maxright) maxright = i+p[i], pos = i;//要及时更新maxright
    }
    printf("%d\n",ans-1);
    return 0;
}