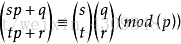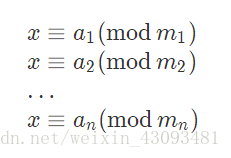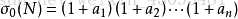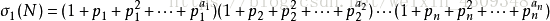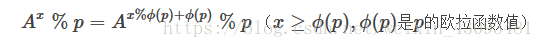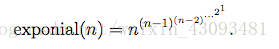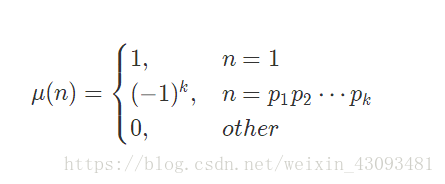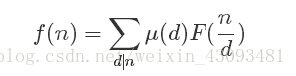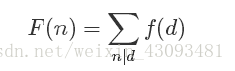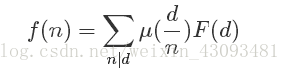ACM-数论完全总结（知识点+模板）

整除的性质
常见定理
模与余
3.1模运算
3.2同余的性质
3.3快速幂
数论重要定理及应用
4.1欧几里得定理
4.2扩展欧几里得
4.3线性同余方程(模线性方程)
4.4中国剩余定理(模线性方程组)
4.5乘法逆元
4.6二次同余方程
4.7唯一分解定理
素数及其相关定理
5.1反素数
5.2素数筛
5.3素性测试
5.4欧拉函数
5.5欧拉降幂公式
5.6积性函数
莫比乌斯相关
6.1莫比乌斯函数
6.2莫比乌斯反演
逆序数
原根
离散对数

一.整除的性质：

1.若a|b <-> -a|b <-> a|-b <-> |a| | |b|
2.若a|b，b|c -> a|c
3.若a|b，a|c -> a|(bx+cy) 其中x，y为任意整数
4.若a|b -> am|bm 其中m为非零整数
5.若a|b，b|a -> b=±a <-> |b|=|a|
6.若a|bc，且a与c互质，则a|b
7.若a|b，a|c，且b与c互质，则a|bc
8.若a|b，c为任意整数，则b|ac
9.对任意整数a，b>0，存在唯一的数对q，r，使a=bq+r，其中0≤r<b，这个事实称为带余除法定理，是整除理论的基础
10.若c|a，c|b，则称c是a，b的公因数。若d是a，b的公因数，d≥0，且d可被a，b的任意公因数整除，则d是a，b的最大公因数。若a，b的最大公因数等于1，则称a，b互素，也称互质。累次利用带余除法可以求出a，b的最大公因数，这种方法常称为辗转相除法。又称欧几里得算法。

二.常见定理：

1.欧拉定理：对于互质的正整数a和n，有a^φ(n) ≡ 1(mod n)
2.费马小定理：若gcd(a,b)=1，则a^(p-1) ≡ 1 (mod n)
3.威尔逊定理：当且仅当p为素数时，(p-1)! ≡ -1 (mod p)
4.卢卡斯定理：这里写图片描述

用于计算组合数取模，其中p必须是素数

三.模与余：

1.模运算：

1.取模运算：a % p（a mod p），表示a除以p的余数。
2.模p加法：(a + b) % p = (a%p + b%p) % p
3.模p减法：(a - b) % p = (a%p - b%p) % p
4.模p乘法：(a * b) % p = ((a % p)*(b % p)) % p
5.幂模p ： (a^b) % p = ((a % p)^b) % p
6.模运算满足结合律、交换律和分配律。
7.a≡b (mod n) 表示a和b模n同余，即a和b除以n的余数相等。

2.同余的性质：

1.反身性：a≡a (mod m)；
2.对称性：若a≡b(mod m)，则b≡a (mod m)；
3.传递性：若a≡b(mod m)，b≡c(mod m)，则a≡c(mod m)；
4.同余式相加：若a≡b(mod m)，c≡d(mod m)，则a c≡b d(mod m)；
5.同余式相乘：若a≡b(mod m)，c≡d(mod m)，则ac≡bd(mod m)。

3.快速幂

3.1快速幂取模

LL pow(LL a, LL n, LL p)    //快速幂 a^n % p
{
    LL ans = 1;
    while(n)
    {
        if(n & 1) ans = ans * a % p;          //若不取模就去掉p
        a = a * a % p;
        n >>= 1;
    }
    return ans;
}

3.2大数快速幂：n>long long (该版本不稳定，建议使用优化版本)

typedef unsigned long long LL;
string str;
int input[10000005];
int output[10000005];
int len;
int sum=1,d=0,k=0;
void to_bin(string str)               //将大整数转换为二进制，转换后为逆序
{
    len=str.size();
    for(int i=0;i<len;i++)
        input[i]=str[i]-'0';
    memset(output,0,sizeof(output));
    sum=1,d=0,k=0;
    while(sum)
    {
        sum = 0;
        for(int i=0;i<len;i++){
            d = input[i] / 2;
            sum += d;
            if(i == (len - 1)){
                output[k++] = input[i] % 2;
            }
            else
                input[i+1] += (input[i]%2)*10;
            input[i] = d;
        }
    }
}
LL pow(LL a, int n[], LL p)    //快速幂 a^n % p
{
    LL ans = 1;
    int i=0;
    while(i<k)
    {
        if(n[i] == 1) ans = ans * a % p;
        a = a * a % p;
        i++;
    }
    return ans;
}
int main()
{
    LL a,b,c;
    while(cin>>a>>str>>c)
    {
        to_bin(str);
        cout<<pow(a,output,c)<<endl;
    }
}

优化版大整数快速幂，O(nlogn)，推荐使用！

#include <bits/stdc++.h>

using namespace std;
const int mod=1e9+7;
long long quick_mod(long long a,long long b)
{
    long long ans=1;
    while(b){
        if(b&1){
            ans=(ans*a)%mod;
            b--;
        }
        b/=2;
        a=a*a%mod;
    }
    return ans;
}//内部也用快速幂
long long quickmod(long long a,char *b,int len)
{
    long long ans=1;
    while(len>0){
        if(b[len-1]!='0'){
            int s=b[len-1]-'0';
            ans=ans*quick_mod(a,s)%mod;
        }
        a=quick_mod(a,10)%mod;
        len--;
    }
    return ans;
}

int main(){
    char s[100050];
    int a;
    while(~scanf("%d",&a))         //求a^s%mod
    {
        scanf("%s",s);
        int len=strlen(s);
        printf("%I64d\n",quickmod(a,s,len));
    }
    return 0;
}

四.数论重要定理及应用

1.欧几里得定理

1.1定义：

gcd(a,b)=gcd(b,a%b)

1.2最大公约数与最小公倍数

int gcd(int a,int b)   //最大公约数
{
    if(b==0)  return a;
    else return gcd(b,a%b);
}

         
int lcm(int a,int b)  //最小公倍数
{
    return a/gcd(a,b)*b;    //防止溢出
}

2.扩展欧几里得

2.1定义：

ax+by=gcd(a,b)=d，在已知a,b的情况下
求解出一组x,y

2.2推导过程：

因为a%b=a-(a/b)b
则有 d=bx1+[a-(a/b)b]y1=bx1+ay1-(a/b)by1=ay1+b(x1-a/by1)
故 x=y1,y=x1-a/by1

2.3性质：

1.若通过扩展欧几里得求出一组特解(x0,y0)，那么有ax0+by0=d.
则方程的通解为，其中k为任意整数
x=x0+k*(b/d)
y=y0-k*(a/d)
2.已知ax+by=d的解，对于ax+by=c的解，c为任意正整数，只有当d|c时才有解
其通解为
x=(c/d)x0+k(b/d)
y=(c/d)y0-k(a/d)

2.4常见用法：

（1）求形如ax+by=c的通解，或从中选取某些特解
（2）求乘法逆元
（3）求解线性同余方程

int exgcd(int a, int b, int &x, int &y) {         //x，y初始为任意值，最后变为一组特解
    if(b == 0) {        //对应最终情况，a=gcd(a,b),b=0,此时x=1，y为任意数
        x = 1;
        y = 0;
        return a;
    }
    int r = exgcd(b, a % b, x, y);      //先递归到最终情况，再反推出初始情况
    int t = x; x = y; y = t - a / b * y;
    return r;     //gcd(a,b)
}

3.线性同余方程(模线性方程)

3.1定义：

形如：ax≡b (mod n)的方程。

3.2性质

定理1：此方程对于未知量x有解当且仅当 gcd(a,n) | b
定理2：d=gcd(a,n)，若d|b，则方程恰好有d个模n不同余的解，否则方程无解
定理3：若x0是方程的任一解，则该方程对模n有d个不同的解，分别为xi=x0+k*(b/d),(k=1,2,…,d-1)

3.3解线性同余方程：

ax≡b (mod n) —> ax+ny=b d=gcd(a,n)，若不满足d|b，则方程无解否则, ax0+ny0=d，利用扩展欧几里得求出一组特解(x0,y0) 然后，x=x0*(b/d)%n就是原方程的一个解且其有d个不同的解，为xi=(x+k*(b/d))%n，0<=k< d

3.3.1最小整数解：

由于一元线性同余方程的通解可以写成res = ( X + i * (b /d) ) (mod n) = X + i * (n/d) + n * y，由于 y 与 i 均为变量因此可以将其合并得到式子 res = X + y * ( n/d) （其中将原式中的 n * y 看做 n/d * d * y，由于y是变量因此可以将 d*y这个整体看为 y）,因此可以得到res = X(mod n/d) ，设m/d 为 t ，其最小正整数解可表示为 (X%t + t) % t。

void RemainderEquation(int a,int b,int n)
{
    int X,Y,d;
    long long res;
    long long min_res;
    d=gcd(a,n);
    exgcd(a,n,X,Y);
    if(b%d == 0)
    {
        X = X * (b / d) % n;//得到同于方程一解
        for(int i = 0 ; i < d; i++)
        {
            res = (X + (i * (b/d))) % n;
            printf("%lld\n",res);             //输出所以解
        }
        min_res=(X%(n/d)+(n/d))%(n/d);    
        cout<<min_res<<endl;       //输出最小解
    }else
    {
        printf("No Sulutions!\n");
    }
}

4.中国剩余定理(模线性方程组)

4.1定义：

对于模线性方程组
这里写图片描述

4.2常规中国剩余定理：各m互质时

int CRT(int a[], int m[], int n) {
    int M = 1;
    int ans = 0;
    for(int i = 1; i <= n; i++) {
        M *= m[i];
    }
    for(int i = 1; i <= n; i++) {
        int x, y;
        int Mi = M / m[i];
        exgcd(Mi, m[i], x, y);
        ans = (ans + Mi * x * a[i]) % M;
    }
    if(ans < 0) ans += M;
    return ans;
}

4.3扩展中国剩余定理：各m不互质

#include<iostream>
#include<cstdio>
#include<climits>
#include<cstring>
#include<algorithm>
using namespace std;
#define LL long long
const int maxn=1e5+5;
int n;
LL exgcd(LL a,LL b,LL &x,LL &y){
    if(!b){x=1,y=0;return a;}
    LL re=exgcd(b,a%b,x,y),tmp=x;
    x=y,y=tmp-(a/b)*y;
    return re;
}
LL m[maxn],a[maxn];      //m为模数集，a为余数集
LL exCRT(){
    LL M=m[1],A=a[1],t,d,x,y;int i;
    for(i=2;i<=n;i++){
        d=exgcd(M,m[i],x,y);//解方程
        if((a[i]-A)%d)return -1;//无解
        x*=(a[i]-A)/d,t=m[i]/d,x=(x%t+t)%t;//求x
        A=M*x+A,M=M/d*m[i],A%=M;//日常膜一膜（划掉）模一模，防止爆
    }
    A=(A%M+M)%M;
    return A;
}
int main()
{
    int i,j;
    while(scanf("%d",&n)!=EOF){
        for(i=1;i<=n;i++)scanf("%lld%lld",&m[i],&a[i]);
        printf("%lld\n",exCRT());
    }
    return 0;
}

5.乘法逆元

5.1定义：

如果有ax≡1(mod n)，则称x是mod n意义下a的乘法逆元。记x=inv（a）或x=a^−1(定义了剩余系中的除法)

5.2性质：

一个数有逆元<=>gcd(a,n)=1，此时逆元存在且唯一

5.3求逆元：

1.扩展欧几里得：ax≡1(mod n)可以等价的转化为ax−ny=1，利用exgcd解方程，并判断gcd(a,n)是否等于1
若等于1，将x调整到1~n-1即可,O(logn)
2.费马小定理：由a^(p−1)≡1(mod p)得a*a^(p−2)≡1(mod p)
所以当模数是一个质数的时候，可以用费马小定理求解，即inv(i)=i^(p−2)(mod p) O(logn)
3.欧拉定理：由a^φ( p) ≡1(mod p)得a^ (φ( p)−1)是a的逆元
适用于模数不是素数

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define LL long long
int inv[1000010];
LL ksm(LL a,LL b,LL mod)      //费马小定理
{
    int ans=1;
    while(b)
    {
        if(b&1) ans=(ans*a)%mod;
        a=(a*a)%mod;
        b>>=1;
    }
    return ans;
}
LL exgcd(LL a,LL b,LL &x,LL &y)   //扩展欧几里得
{
    if(!b)
    {
        x=1;
        y=0;
        return a;
    }
    LL GCD=exgcd(b,a%b,x,y);
    LL tmp=x;
    x=y;
    y=tmp-a/b*y;
    return GCD;
}
LL inv1(LL a,LL mod)//扩展欧几里得求逆元
{
    LL x,y;
    LL d=exgcd(a,mod,x,y);
    if(d==1) return (x%mod+mod)%mod;
    return -1;
}
LL inv2(LL a,LL mod)//费马小定理
{
    return ksm(a,mod-2,mod);
}
void inv3(LL mod)//线性递推求1~n的所以逆元
{
    inv[1]=1;
    for(int i=2;i<=mod-1;i++)
    {
        inv[i]=(mod-mod/i)*inv[mod%i]%mod;
        cout<<inv[i]<<" ";
    }
}
int main()
{
    LL n,mod;
    while(cin>>n>>mod)
    {
        cout<<inv1(n,mod)<<" "<<inv2(n,mod)<<endl;
        inv3(mod);
    }
}

6.二次同余方程

6.1定义：

x^2≡n(mod p)，已知n和p求一个x满足该式，即x满足x^2=n+kp,k为整数，则称n是模p的二次剩余

6.2常见用法：

x^2≡n(mod p) -> x≡sqrt(n)(mod p) 即若该二次同余方程有解，则n可在mod p的意义下开根号

6.3求解二次同余方程：p必须为奇质数

#include <iostream>   
#include <ctime>
using namespace std;
typedef long long LL;
#define random(a,b) (rand()%(b-a+1)+a)
LL quick_mod(LL a, LL b, LL c) { LL ans = 1; while (b) { if (b % 2 == 1)ans = (ans*a) % c; b /= 2; a = (a*a) % c; }return ans; }
LL p;
LL w;//二次域的D值
bool ok;//是否有解
struct QuadraticField//二次域
{
    LL x, y;
    QuadraticField operator*(QuadraticField T)//二次域乘法重载
    {
        QuadraticField ans;
        ans.x = (this->x*T.x%p + this->y*T.y%p*w%p) % p;
        ans.y = (this->x*T.y%p + this->y*T.x%p) % p;
        return ans;
    }
    QuadraticField operator^(LL b)//二次域快速幂
    {
        QuadraticField ans;
        QuadraticField a = *this;
        ans.x = 1;
        ans.y = 0;
        while (b)
        {
            if (b & 1)
            {
                ans = ans*a;
                b--;
            }
            b /= 2;
            a = a*a;
        }
        return ans;
    }
};
LL Legender(LL a)//求勒让德符号
{
    LL ans=quick_mod(a, (p - 1) / 2, p);
    if (ans + 1 == p)//如果ans的值为-1，%p之后会变成p-1。
        return -1;
    else
        return ans;
}
LL Getw(LL n, LL a)//根据随机出来a的值确定对应w的值
{
    return ((a*a - n) % p + p) % p;//防爆处理
}
LL Solve(LL n)
{
    LL a;
    if (p == 2)//当p为2的时候，n只会是0或1，然后0和1就是对应的解
        return n;
    if (Legender(n) == -1)//无解
        ok = false;
    srand((unsigned)time(NULL));
    while (1)//随机a的值直到有解
    {
        a = random(0, p - 1);
        w = Getw(n, a);
        if (Legender(w) == -1)
            break;
    }
    QuadraticField ans,res;
    res.x = a;
    res.y = 1;//res的值就是a+根号w
    ans = res ^ ((p + 1) / 2);
    return ans.x;
}
int main()
{
    LL n,ans1,ans2;
    while (scanf("%lld%lld",&n,&p)!=EOF)
    {
        ok = true;
        n %= p;
        ans1 = Solve(n);
        ans2 = p - ans1;//一组解的和是p
        if (!ok)
        {
            printf("No root\n");
            continue;
        }
        if (ans1 == ans2)
            printf("%lld\n", ans1);
        else
            printf("%lld %lld\n", ans1, ans2);
    }
}

7.唯一分解定理：

7.1定义：

任何一个大于1的自然数 N ，都可以唯一分解成有限个质数的乘积，这里均为质数，其诸指数是正整数。

7.2性质：

1.重要推理：如果质数p是ab的因子，那么p或者是a的因子，或者是b的因子
2.N的因子个数为：这里写图片描述
3.N的全体正因数之和为：

7.3唯一分解定理完全模板：O(φ(n))

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod=1e9+7;
bool check[100005];
int prime[100005];     //储存第i个素数
int tot=0;
LL pow(LL a, LL n, LL p)    //快速幂 a^n % p
{
    LL ans = 1;
    while(n)
    {
        if(n & 1) ans = ans * a % p;          //若不取模就去掉p
        a = a * a % p;
        n >>= 1;
    }
    return ans;
}
void getprime(int n)
{
    memset(check, 0, sizeof(check));  // 标记数组初始化，初始均为 0
    tot = 0;  // tot 初始为 0，用来记录质数总个数
    for (int i = 2; i <= n; ++i) {  // 从 2 开始枚举
        if (!check[i]) {  // 如果 i 没有被划去，则 i 为质数，加入质数表中
            prime[++tot] = i;
        }
        for (int j = 1; j <= tot; ++j) {  // 划去 i 与所有已筛出的质数的乘积
            if (i * prime[j] > n) {  // 判断合数是否在区间内
                break;
            }
            check[i * prime[j]] = 1;  // 划去在区间内的合数
            if (i % prime[j] == 0) {  // 保证合数只被其最小的质因子划去，提高筛选效率
                break;
            }
        }
    }
}
void getans(int n)   
{
    int a[10000],b[100005],c[100005],cnt=0,cnt2=0,t;
    t=n;
    for(int i=1;prime[i]*prime[i]<=n;i++)
    {
        if(n%prime[i]==0)
        {
            a[cnt]=prime[i];
            while(n%prime[i]==0)
            {
                c[cnt2++]=prime[i];
                b[cnt]++;
                n/=prime[i];
            }
            cnt++;
        }
    }
    if(n!=1)
    {
        a[cnt]=n;
        b[cnt]=1;
        c[cnt2]=n;
        cnt2++;
        cnt++;
    }
    int cnt_factor=1;             //因数的个数
    long long sum_factor=1;       //全部因数之和
    for(int i=0;i<cnt;i++)
        cnt_factor*=(b[i]+1);
    cout<<cnt_factor<<endl;           //因数的个数
    for(int i=0;i<cnt;i++)
    {
        LL cur=0;
        for(int j=0;j<=b[i];j++)
        {
            cur+=pow(a[i],j,mod);
        }
        sum_factor*=cur;
    }
    cout<<sum_factor-t<<endl;       //全部因数之和
    for(int i=0;i<cnt;i++)              //幂指形式表示
        cout<<a[i]<<"^"<<b[i]<<" ";
    cout<<endl;
    for(int i=0;i<cnt2;i++)         //连乘形式表示
        cout<<c[i]<<" ";
    cout<<endl;
}
int main()
{
    int n;
    getprime(10000);
    scanf("%d",&n);
    getans(n);
    return 0;
}

7.4N!的素因子分解：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn = 10000010;
int prime[maxn],cnt;
int ans[maxn];
bool is[maxn];
void init(int n)
{
    cnt=0;
    memset(is,1,sizeof(is));
    memset(ans,0,sizeof(ans));
    memset(prime,0,sizeof(prime));
    for(int i=2;i<=n;i++){
        if(is[i]){
            prime[cnt++]=i;
            for(int j=i+i;j<=n;j+=i)
                is[j]=0;
        }
    }
}
int fen(int n,int p)
{
    if(n==0) return 0;
    return fen(n/p,p)+n/p;
}
int main()
{
    int n;
    while(~scanf("%d",&n)){
        init(n);
        for(int i=0;i<cnt;i++)
            ans[i]=fen(n,prime[i]);
        for(int i=0;i<cnt;i++)
            printf("%d^%d\n",prime[i],ans[i]);
    }
    return 0;
}

7.5Pollard-rho 大数因式分解

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<time.h>
#include<iostream>
#include<algorithm>
using namespace std;
//****************************************************************
// Miller_Rabin 算法进行素数测试
//速度快，而且可以判断 <2^63的数
//****************************************************************
const int S=20;//随机算法判定次数，S越大，判错概率越小
//计算 (a*b)%c.   a,b都是long long的数，直接相乘可能溢出的
//  a,b,c <2^63
long long mult_mod(long long a,long long b,long long c)
{
    a%=c;
    b%=c;
    long long ret=0;
    while(b)
    {
        if(b&1){ret+=a;ret%=c;}
        a<<=1;
        if(a>=c)a%=c;
        b>>=1;
    }
    return ret;
}
//计算  x^n %c
long long pow_mod(long long x,long long n,long long mod)//x^n%c
{
    if(n==1)return x%mod;
    x%=mod;
    long long tmp=x;
    long long ret=1;
    while(n)
    {
        if(n&1) ret=mult_mod(ret,tmp,mod);
        tmp=mult_mod(tmp,tmp,mod);
        n>>=1;
    }
    return ret;
}
//以a为基,n-1=x*2^t      a^(n-1)=1(mod n)  验证n是不是合数
//一定是合数返回true,不一定返回false
bool check(long long a,long long n,long long x,long long t)
{
    long long ret=pow_mod(a,x,n);
    long long last=ret;
    for(int i=1;i<=t;i++)
    {
        ret=mult_mod(ret,ret,n);
        if(ret==1&&last!=1&&last!=n-1) return true;//合数
        last=ret;
    }
    if(ret!=1) return true;
    return false;
}
// Miller_Rabin()算法素数判定
//是素数返回true.(可能是伪素数，但概率极小)
//合数返回false;
bool Miller_Rabin(long long n)
{
    if(n<2)return false;
    if(n==2)return true;
    if((n&1)==0) return false;//偶数
    long long x=n-1;
    long long t=0;
    while((x&1)==0){x>>=1;t++;}
    for(int i=0;i<S;i++)
    {
        long long a=rand()%(n-1)+1;//rand()需要stdlib.h头文件
        if(check(a,n,x,t))
            return false;//合数
    }
    return true;
}
//************************************************
//pollard_rho 算法进行质因数分解
//************************************************
long long factor[100];//质因数分解结果（刚返回时是无序的）
int tol;//质因数的个数。数组小标从0开始
long long gcd(long long a,long long b)
{
    if(a==0)return 1;//???????
    if(a<0) return gcd(-a,b);
    while(b)
    {
        long long t=a%b;
        a=b;
        b=t;
    }
    return a;
}
long long Pollard_rho(long long x,long long c)
{
    long long i=1,k=2;
    long long x0=rand()%x;
    long long y=x0;
    while(1)
    {
        i++;
        x0=(mult_mod(x0,x0,x)+c)%x;
        long long d=gcd(y-x0,x);
        if(d!=1&&d!=x) return d;
        if(y==x0) return x;
        if(i==k){y=x0;k+=k;}
    }
}
//对n进行素因子分解
void findfac(long long n)
{
    if(Miller_Rabin(n))//素数
    {
        factor[tol++]=n;
        return;
    }
    long long p=n;
    while(p>=n)p=Pollard_rho(p,rand()%(n-1)+1);
    findfac(p);
    findfac(n/p);
}
int main()
{
    //srand(time(NULL));//需要time.h头文件//POJ上G++不能加这句话
    long long n;
    while(scanf("%I64d",&n)!=EOF)
    {
        tol=0;
        findfac(n);
        for(int i=0;i<tol;i++)printf("%I64d ",factor[i]);      //输出因子
        printf("\n");
    }
    return 0;
}

五.素数：

1.反素数：

1.1定义

对于任何正整数x，其约数的个数记作g(x)。例如g(1)=1、g(6)=4。
如果某个正整数x满足：g(x)>g(i) 0 < i < x，则称x为反质数。例如，整数1，2，4，6等都是反质数。
即是区间中约数最多的那个数

1.2性质：

1.一个反素数的质因子必然是从2开始连续的质数
2.N=p1^a1 *p2^a2 *…*pn^an，必然有a1>=a2>=a3…>=an

1.3常见用法：

（1）给定一个数N，求一个最小的正整数X，使得X的约数个数为N

#include <bits/stdc++.h>
#define inf (0x3f3f3f3f)
typedef long long int LL;
LL pr, mx, BEGIN, END = 1e18;
const int maxn=50+20;
int prime[maxn];//这个记得用int，他保存的是质数，可以不用开maxn那么大
bool check[maxn];
int total;
int n;
void initprime() {
    for (int i=2; i<=maxn-20; i++) {
        if (!check[i]) { //是质数了
            prime[++total]=i;//只能这样记录，因为后面要用
        }
        for (int j=1; j<=total; j++) { //质数或者合数都进行的
            if (i*prime[j]>maxn-20) break;
            check[i*prime[j]]=1;
            if (i%prime[j]==0) break;
            //关键，使得它只被最小的质数筛去。例如i等于6的时候。
            //当时的质数只有2,3,5。6和2结合筛去了12，就break了
            //18留下等9的时候，9*2=18筛去
        }
    }
    return ;
}
void dfs(LL curnum, int cnt, int depth, int up) {
    if (depth > total) return ; // 越界了，用不到那么多素数
    if ((cnt > mx || cnt == mx && pr > curnum) && cnt == n) {
        pr = curnum;
        mx = cnt;
    }
    for (int i = 1; i <= up; ++i) { //枚举有多少个prime[depth]
        if (END / curnum < prime[depth]) return ;
        if ((BEGIN - 1) / curnum == END / curnum) return ; //区间不存在这个数的倍数
        curnum *= prime[depth]; //一路连乘上去
        dfs(curnum, cnt * (i + 1), depth + 1, i); // 2^2 * 3， 3最多2个
    }
}
void work() {
    cin >> n;
    dfs(1, 1, 1, 64);
    cout << pr << endl;
    return ;
}
int main() {
    initprime();
    work();
    return 0;
}

（2）求出1~N中约数个数最多且数值最小的这个数

#include <bits/stdc++.h>
#define inf (0x3f3f3f3f)
typedef long long int LL;
LL pr, mx, BEGIN, END;
const int maxn=50+20;
int prime[maxn];
bool check[maxn];
int total;
void initprime() {
    for (int i=2; i<=maxn-20; i++) {
        if (!check[i]) {
            prime[++total]=i;
        }
        for (int j=1; j<=total; j++) {
            if (i*prime[j]>maxn-20) break;
            check[i*prime[j]]=1;
            if (i%prime[j]==0) break;
        }
    }
    return ;
}
void dfs(LL curnum, int cnt, int depth, int up) {
    if (depth > total) return ; //
    if ((cnt > mx || cnt == mx && pr > curnum) && curnum >= BEGIN) {
        pr = curnum;
        mx = cnt;
    }
    for (int i = 1; i <= up; ++i) {
        if (END / curnum < prime[depth]) return ;
        if ((BEGIN - 1) / curnum == END / curnum) return ; //
        curnum *= prime[depth]; //
        dfs(curnum, cnt * (i + 1), depth + 1, i);
    }
}
void work() {
    pr = 0, mx = 0, BEGIN = 1;
    cin >> END;
    dfs(1, 1, 1, 64);
    cout << pr << " " << mx << endl;
    return ;
}
int main() {
    initprime();
    int t;
    cin >> t;
    while (t--) {
        work();
    }
    return 0;
}

（3）求[begin,end]中最小的反素数：

#include <bits/stdc++.h>
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
LL pr, mx, BEGIN, END = 1e18;
const int maxn=1e6+20;
int prime[maxn];//这个记得用int，他保存的是质数，可以不用开maxn那么大
bool check[maxn];
int total;
int n;
void initprime() {
    for (int i=2; i<=maxn-20; i++) {
        if (!check[i]) { //是质数了
            prime[++total]=i;//只能这样记录，因为后面要用
        }
        for (int j=1; j<=total; j++) { //质数或者合数都进行的
            if (i*prime[j]>maxn-20) break;
            check[i*prime[j]]=1;
            if (i%prime[j]==0) break;
            //关键，使得它只被最小的质数筛去。例如i等于6的时候。
            //当时的质数只有2,3,5。6和2结合筛去了12，就break了
            //18留下等9的时候，9*2=18筛去
        }
    }
    return ;
}
LL mypow (LL a, LL b) {
    LL ans = 1;
    while (b) {
        if (b & 1) {
            ans *= a;
        }
        a *= a;
        b >>= 1;
    }
    return ans;
}
void dfs (int cur,int cnt,LL now,LL from) {
    LL t=from*(cnt+1);//现在一共拥有的因子数
    if (now>=BEGIN && t>mx || t==mx && pr>now && now >= BEGIN) { //有得换了
        mx=t;
        pr=now;
    }
    for (int i=cur; i<=total; ++i) { //枚举每一个素数
        LL temp = now*prime[i];
        if (END / now < prime[i]) return ; //这个数超出范围了
        if (i == cur) { //没有变，一直都是用这个数.2^k
            dfs(cur,cnt+1,temp,from);//唯一就是from没变，一直都是用着2，不是新质数
        } else { //枚举新质数了。
            LL k = (cnt+1)*from; //现在有K个因子
            LL q=(LL)(log(END/now) / log(prime[cur])); //2*3插入5时，用的是3来放缩
            LL add = k*mypow(2,q);
            if (add < mx) return ; //这里等于mx不return，可以输出minpr
            if ((BEGIN-1)/now == END/now) return; //不存在now的倍数
            if (END/now > prime[total]) { //试着给他乘上一个大素数 [999991,999991]
                if ( k*2 > mx ) { //乘以一个大素数，因子数*2
                    pr = END;//如果只有一个大素数[1e9+7,le9+7]那么，就是端点值
                    //否则，是2*3*5*bigprime的话，结果不是最优的，
                    mx = k*2;
                }
            }
            dfs(i,1,temp,k);
        }
    }
    return;
}
void work() {
    cin >> BEGIN >> END;
    dfs(1,0,1,1);
    cout << mx << endl;
    return ;
}
int main() {
    initprime();
    work();
    return 0;
}

2.素数筛：

2.1线性素数筛：O(n)

bool check[100005];
int prime[100005];     //储存第i个素数
void getprime(int n)
{
    memset(check, 0, sizeof(check));  // 标记数组初始化，初始均为 0
    int tot = 0;  // tot 初始为 0，用来记录质数总个数
    for (int i = 2; i <= n; ++i) {  // 从 2 开始枚举
        if (!check[i]) {  // 如果 i 没有被划去，则 i 为质数，加入质数表中
            prime[++tot] = i;
        }
        for (int j = 1; j <= tot; ++j) {  // 划去 i 与所有已筛出的质数的乘积
            if (i * prime[j] > n) {  // 判断合数是否在区间内
                break;
            }
            check[i * prime[j]] = 1;  // 划去在区间内的合数
            if (i % prime[j] == 0) {  // 保证合数只被其最小的质因子划去，提高筛选效率
                break;
            }
        }
    }

2.2埃氏素数筛：O(nloglogn)

vector<int>prime;        //其中存储2-n的所有素数
bool is_prime[MAXN]   //存储第i项是否为素数 
void find_prime(int n)
{
    int p=0;
    for(int i=2;i<=n;i++)
        is_prime[i]=true;
    is_prime[0]=is_prime[1]=false;
    for(int i=2;i<=n;i++)
    {
        if(is_prime[i])
        {
            prime.push_back(i);
            for(int j=2*i;j<=n;j+=i)
                is_prime[j]=false;
        }
    }
}

3.素性测试：

3.1数据量较小：

直接用素数筛+hash表即可

3.2数据量较大：

miller_rabin：概率算法，能处理10^19范围数

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<time.h>
#include<iostream>
#include<algorithm>
using namespace std;
const int S=20;//随机算法判定次数，S越大，判错概率越小
//计算 (a*b)%c.   a,b都是long long的数，直接相乘可能溢出的
//  a,b,c <2^63
long long mult_mod(long long a,long long b,long long c)
{
    a%=c;
    b%=c;
    long long ret=0;
    while(b)
    {
        if(b&1){ret+=a;ret%=c;}
        a<<=1;
        if(a>=c)a%=c;
        b>>=1;
    }
    return ret;
}
//计算  x^n %c
long long pow_mod(long long x,long long n,long long mod)//x^n%c
{
    if(n==1)return x%mod;
    x%=mod;
    long long tmp=x;
    long long ret=1;
    while(n)
    {
        if(n&1) ret=mult_mod(ret,tmp,mod);
        tmp=mult_mod(tmp,tmp,mod);
        n>>=1;
    }
    return ret;
}
//以a为基,n-1=x*2^t      a^(n-1)=1(mod n)  验证n是不是合数
//一定是合数返回true,不一定返回false
bool check(long long a,long long n,long long x,long long t)
{
    long long ret=pow_mod(a,x,n);
    long long last=ret;
    for(int i=1;i<=t;i++)
    {
        ret=mult_mod(ret,ret,n);
        if(ret==1&&last!=1&&last!=n-1) return true;//合数
        last=ret;
    }
    if(ret!=1) return true;
    return false;
}
// Miller_Rabin()算法素数判定
//是素数返回true.(可能是伪素数，但概率极小)
//合数返回false;
bool Miller_Rabin(long long n)
{
    if(n<2)return false;
    if(n==2)return true;
    if((n&1)==0) return false;//偶数
    long long x=n-1;
    long long t=0;
    while((x&1)==0){x>>=1;t++;}
    for(int i=0;i<S;i++)
    {
        long long a=rand()%(n-1)+1;//rand()需要stdlib.h头文件
        if(check(a,n,x,t))
            return false;//合数
    }
    return true;
}
int main()
{
    long long n;
    while(scanf("%I64d",&n)!=EOF)
    {
        if(Miller_Rabin(n))printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

4.欧拉函数：

4.1定义：

互质：gcd(a,b)=1，则a，b互质
欧拉函数φ(n):小于等于n的所有数中与n互质数的个数

4.2性质：

1.对于质数p， φ( p) = p - 1。注意φ(1)=1
2. 若m,n互质，φ(mn)=φ(m)φ(n)
3. 当n为奇数时，φ(2n)=φ(n)
4.当n大于2时，所有φ(n)都是偶数
5.当n大于6时，所有φ(n)都是合数

6.欧拉定理：对于互质的正整数a和n，有a^φ(n) ≡ 1 mod n
7.费马小定理：若gcd(a,b)=1，则a^(p-1)=1 mod n
8.欧拉定理推论：小于等于n的数中，与n互质数的总和为：φ(n)*n/2 (n>1)

4.3求一个数的欧拉函数：O(sqrt(n))

//直接求解欧拉函数  
  int euler(int n){ //返回euler(n)   
       int res=n,a=n;  
       for(int i=2;i*i<=a;i++){  
           if(a%i==0){  
               res=res/i*(i-1);//先进行除法是为了防止中间数据的溢出   
               while(a%i==0) a/=i;  
           }  
       }  
      if(a>1) res=res/a*(a-1);  
      return res;  
}

4.4求1~n每个数的欧拉函数：O(nlogn)

void Init(){     
     euler[1]=1;    
     for(int i=2;i<Max;i++)    
       euler[i]=i;    
     for(int i=2;i<Max;i++)    
        if(euler[i]==i)    
           for(int j=i;j<Max;j+=i)    
              euler[j]=euler[j]/i*(i-1);//先进行除法是为了防止中间数据的溢出
}

5.欧拉降幂公式

5.1定义：

这里写图片描述

5.2利用欧拉降幂公式求exponial(n）

这里写图片描述

#include <iostream>
using namespace std;

typedef long long ll;  
ll n,m,ans;

ll euler(ll n){ //返回euler(n) ，计算欧拉函数值
     ll res=n,a=n;  
     for(ll i=2;i*i<=a;i++){  
         if(a%i==0){  
             res=res/i*(i-1);//先进行除法是为了防止中间数据的溢出   
             while(a%i==0) a/=i;  
         }  
     }  
     if(a>1) res=res/a*(a-1);  
     return res;  
}
ll fast_mod(ll x,ll n,ll Max)  //快速幂
{  
    ll res=1;  
    while(n>0)  
    {  
        if(n & 1)  
            res=(res*x)%Max;  
        x=(x*x)%Max;  
        n >>= 1;  
    }  
    return res;  
}
ll func(ll n,ll m){      //循环求解
    
    if(m==1) return 0;
    
    if(n<=5){
        ll ans=1;
        for(int i=1;i<=n;i++){
            ans=fast_mod(i,ans,m);
        }
        return ans;
    }else{
        ll phi=euler(m);
        ll z=func(n-1,phi);
        ans=fast_mod(n,phi+z,m);
    }
    return ans;
    
}
void solve(){        //计算exponial（n）
    scanf("%lld%lld",&n,&m);
    printf("%lld\n",func(n,m));
}
int main(){
    solve();
    
    return 0;
}

6.积性函数

6.1定义：

积性函数：若gcd(a,b)=1，且满足f(ab)=f(a)f(b)，则称f(x)为积性函数
完全积性函数：对于任意正整数a，b，都满足f(ab)=f(a)f(b)，则称f(x)为完全积性函数

6.2性质:

1.若f(n),g(n)均为积性函数，则函数h(n)=f(n)g(n)也是积性函数
2.若f(n)为积性函数，则函数也是积性函数，反之一样
3.任何积性函数都能应用线性筛，在O(n)时间内求出1~n项

六.莫比乌斯

1.莫比乌斯函数：

1.1定义：

这里写图片描述

1.2性质：

1.对于任意正整数n，∑(d|n) μ(d)=[n=1]。（[n=1]表示只有当n=1成立时，返回值为1；否则，值为0；(这个就是用μ是容斥系数的性质可以证明)(PS:这一条性质是莫比乌斯反演中最常用的)
2.对于任意正整数n，∑(d|n) μ(d)/d=ϕ(n)/n。（这个性质很奇妙，它把欧拉函数和莫比乌斯函数结合起来）

1.3求μ函数：O(n)

void get_mu(int n)
{
    mu[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!vis[i]){prim[++cnt]=i;mu[i]=-1;}
        for(int j=1;j<=cnt&&prim[j]*i<=n;j++)
        {
            vis[prim[j]*i]=1;
            if(i%prim[j]==0)break;
            else mu[i*prim[j]]=-mu[i];
        }
    }
}

2.莫比乌斯反演：

2.1定义:

若F(x)和f(x)满足：
这里写图片描述
则有：

或者
若F(x)和f(x)满足：

则有：

2.2性质：

1.若n>1且n为正整数，则有这里写图片描述，若n=1，则该式为1
2.对于任意正整数n均有：

七.逆序数：

1.定义:

在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数

#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
const int N=100050;
int n;
long long c[N];      //c[n]表示a[1~n]的和，a数组省略
struct node
{
    int val,pos;
}a[100005];
int lowbit(int x)       //求2^k
{
    return x & -x;
}
long long getsum(int n)   //区间查询，求a[1~n]的和
{
    long long res = 0;
    while(n>0)
    {
        res+=c[n];
        n=n-lowbit(n);
    }
    return res;
}
int change(int x)  //单点更新，将c[x]的值加1
{
     while(x<=n)
     {
         c[x]++;
         x+=lowbit(x);
     }
}
bool cmp(node a,node b)         //包含相同数
{
    if(a.val!=b.val)
        return a.val>b.val;
    return a.pos>b.pos;
}
int main()
{
    std::ios::sync_with_stdio(false);
    while(cin>>n)
    {
        memset(c,0,sizeof(c));
        for(int i=1;i<=n;i++)
        {
            cin>>a[i].val;
            a[i].pos=i;
        }
        sort(a+1,a+n+1,cmp);
        long long cnt=0;
        for(int i=1;i<=n;i++)
        {
            change(a[i].pos);                     //修改最大数位置的值
            cnt+=getsum(a[i].pos-1);     //最大数位置之前的所有位置和，即区间求和，可知比当前数小的数有多少个
        }
        cout<<cnt<<endl;
    }
    return 0;
}

八.原根：

1.定义:

阶：a^t ≡ 1(mod m) ,其中m>1，且gcd(a,m)=1，使该式成立的最小的正整数t称为a对模m的阶，记作δm(a)
原根：如果a的阶(mod m)为ϕ(m), 则称a为m的一个原根。
即若δm(a)=ϕ(m), 则称a为m的一个原根。

2.性质：

1.具有原根的数字仅有以下几种形式:2,4,p^n ,2⋅p^n(p是奇质数)
2.一个数的最小原根的大小不超过 m^(1/4)
3.若g是m的一个原根，那么g^d是m的原根的充分必要条件是gcd(d,Φ(m))=1, 由此可推知一个数的原根个数为Φ(Φ(m))个

推论1 若d|(p−1),则x^d≡1(mod p)恰有d个解
推论2 若p为素数,d|(p−1),则阶为d的最小剩余(mod p)的个数为ϕ(d)。

3.求原根：

1.判断一个数是否有原根。(通过性质1,枚举质数即可)
2.求得最小原根。(通过性质2,依次枚举2～m^(1/4)判断即可)
3.求出所有原根。(通过性质3,枚举次数d即可)

求质数p的最小原根：

#include <iostream>  
#include <cstdlib>  
#include <cstring>  
#include <cstdio>  
using namespace std;  
int P;  
const int NUM = 32170;  
int prime[NUM/4];  
bool f[NUM];  
int pNum = 0;  
void getPrime()//线性筛选素数  
{  
    for (int i = 2; i < NUM; ++ i)  
    {  
        if (!f[i])  
        {  
            f[i] = 1;  
            prime[pNum++] = i;  
        }  
        for (int j = 0; j < pNum && i*prime[j] < NUM; ++ j)  
        {  
            f[i*prime[j]] = 1;  
            if (i%prime[j] == 0)  
            {  
                break;  
            }  
        }  
    }  
}  
LL getProduct(int a,int b,int P)//快速求次幂mod  
{  
    LL ans = 1;  
    LL tmp = a;  
    while (b)  
    {  
        if (b&1)  
        {  
            ans = ans*tmp%P;  
        }  
        tmp = tmp*tmp%P;  
        b>>=1;  
    }  
    return ans;  
}  
  
bool judge(int num)//求num的所有的质因子  
{  
    int elem[1000];  
    int elemNum = 0;  
    int k = P - 1;  
    for (int i = 0; i < pNum; ++ i)  
    {  
        bool flag = false;  
        while (!(k%prime[i]))  
        {  
            flag = true;  
            k /= prime[i];  
        }  
        if (flag)  
        {  
            elem[elemNum ++] = prime[i];  
        }  
        if (k==1)  
        {  
            break;  
        }  
        if (k/prime[i]<prime[i])  
        {  
            elem[elemNum ++] = prime[i];  
            break;  
        }  
    }  
    bool flag = true;  
    for (int i = 0; i < elemNum; ++ i)  
    {  
        if (getProduct(num,(P-1)/elem[i],P) == 1)  
        {  
            flag = false;  
            break;  
        }  
    }  
    return flag;  
}  
int main()  
{  
      
    getPrime();  
    while (cin >> P)  
    {  
        for (int i = 2;;++i)  
        {  
            if (judge(i))  
            {  
                cout << i<< endl;  
                break;  
            }  
        }  
    }  
    return 0;  
}

九.离散对数：

1.定义：

g是m的一个原根，对于满足gcd(k,m)=1的k，若g^t≡k (mod m)成立，则称t是k关于g的离散对数
且t为一个最小剩余(mod φ(m))，记作ind(g)(k)，类比于log(g)(k)，不过这里对φ(m)取模了
例如，m=5，有一个原根g=2
此时有，2^0 ≡1，2^1 ≡2，2^2 ≡4，2^3 ≡3 (mod 5)
所以有，ind(2)(1)=0，ind(2)(2)=1，ind(2)(4)=2，ind(2)(3)=3

2.性质：

1.ind(g)(ab) ≡ ind(g)(a)+ind(g)(b) (mod φ(m))
2.ind(g)(a^n) ≡ n*ind(g)(a) (mod φ(m))

3.求离散对数：

a^x≡b (mod p) ，已知a,b,p，求该同余方程x的最小正整数解，显然当a为p的一个原根时，x即为b关于a的离散对数(mod p)

3.1扩展BSGS:

求 a^x ≡ b (mod p) 中的 x值 – 此处p可为合数也可为素数 | 实际运用中用自己的hash表代替map可防TLE

LL exBSGS(LL a, LL b, LL p) {
    a %= p; b %= p;
    LL ret = 1;
    for(LL i = 0; i <= 50; ++i) {
        if(ret == b) return i;
        ret = (ret*a) % p;
    }//枚举比较小的i
    LL x,y,d, v = 1, cnt = 0;
    while((d = gcd(a, p)) != 1) {
        if(b % d) return -1;
        b /= d, p /= d;
        v = (v * (a/d)) % p;
        ++cnt;
    }//约分直到(a, p) == 1
    map<LL, LL> h;
    LL m = ceil(sqrt(p)), t = 1;
    for(LL i = 0; i < m; ++i) {
        if(h.count(t)) h[t] = min(h[t], i);
        else h[t] = i;
        t = (t*a) % p;
    }
    for(LL i = 0; i < m; ++i) {
        d = extgcd(v, p, x, y);
        x = (x* (b/d) % p + p) % p;
        if(h.count(x)) return i*m + h[x] + cnt;
        v = (v*t) % p;
    }
    return -1;
}

posted @ 2018-08-30 23:51 floatingcloak 阅读(1153) 评论(0) 编辑收藏举报

刷新页面返回顶部

floatingcloak

ACM-数论完全总结（知识点+模板）

目录：

一.整除的性质：

二.常见定理：

三.模与余：

1.模运算：

2.同余的性质：

3.快速幂

3.1快速幂取模

3.2大数快速幂：n>long long (该版本不稳定，建议使用优化版本)

四.数论重要定理及应用

1.欧几里得定理

1.1定义：

1.2最大公约数与最小公倍数

2.扩展欧几里得

2.1定义：

2.2推导过程：

2.3性质：

2.4常见用法：

3.线性同余方程(模线性方程)

3.1定义：

3.2性质

3.3解线性同余方程：

3.3.1最小整数解：

4.中国剩余定理(模线性方程组)

4.1定义：

4.2常规中国剩余定理：各m互质时

4.3扩展中国剩余定理：各m不互质

5.乘法逆元

5.1定义：

5.2性质：

5.3求逆元：

6.二次同余方程

6.1定义：

6.2常见用法：

6.3求解二次同余方程：p必须为奇质数

7.唯一分解定理：

7.1定义：

7.2性质：

7.3唯一分解定理完全模板：O(φ(n))

7.4N!的素因子分解：

7.5Pollard-rho 大数因式分解

五.素数：

1.反素数：

1.1定义

1.2性质：

1.3常见用法：

2.素数筛：

2.1线性素数筛：O(n)

2.2埃氏素数筛：O(nloglogn)

3.素性测试：

3.1数据量较小：

3.2数据量较大：

4.欧拉函数：

4.1定义：

4.2性质：

4.3求一个数的欧拉函数：O(sqrt(n))

4.4求1~n每个数的欧拉函数：O(nlogn)

5.欧拉降幂公式

5.1定义：

5.2利用欧拉降幂公式求exponial(n）

6.积性函数

6.1定义：

6.2性质:

六.莫比乌斯

1.莫比乌斯函数：

1.1定义：

1.2性质：

1.3求μ函数：O(n)

2.莫比乌斯反演：

2.1定义:

2.2性质：

七.逆序数：

1.定义:

八.原根：

1.定义:

2.性质：

3.求原根：

求质数p的最小原根：