【LeetCode-二分查找】寻找两个正序数组的中位数
题目描述
给定两个大小为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。
请你找出这两个正序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
示例：
nums1 = [1, 3]
nums2 = [2]
则中位数是 2.0
nums1 = [1, 2]
nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5
题目链接： https://leetcode-cn.com/problems/median-of-two-sorted-arrays/
思路
因为题目要求算法的时间复杂度为 O(log(m + n))，log 的时间复杂度一般是使用二分查找来做。
因为两个数组是有序的，所以我们可以一半一半地对数组进行寻找。假设两个数组如下
图来自这篇题解。
假设我们要找第 k = 7 小的数字，则我们可以比较 nums1[k/2] 和 nums2[k/2] 之间的大小，如果 nums2[k/2]<nums1[k/2]，因为数组是升序的，则 nums2[k/2] 之前的数字都不会是第 k 小的数字，可以直接删除
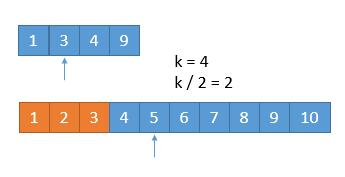
黄色部分表示已删除。此时我们已经删除了 7/2 = 3 个数字，所以接下来我们要找第 k = 7 - 3 = 4 小的数字。同样地，我们继续比较 nums1[k/2] 和 nums2[k/2] 之间的大小，根据大小关系判断如何删除元素。
这个过程会有一个问题，因为我们每次都是比较两个数组的第 k/2 个元素，但可能会出现数组长度小于 k/2 的情况，如下
解决办法就是我们取 min(k/2, len) - 1 对应的元素进行比较，len 为数组的剩余长度。
代码如下：
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size();
int n = nums2.size();
int left = (m+n+1)/2;
int right = (m+n+2)/2;
return (find(nums1, 0, m-1, nums2, 0, n-1, left) + find(nums1, 0, m-1, nums2, 0, n-1, right)) / 2;
}
double find(vector<int>& nums1, int left1, int right1, vector<int>& nums2, int left2, int right2, int k){
int len1 = right1-left1+1;
int len2 = right2-left2+1;
if(len1>len2) return find(nums2, left2, right2, nums1, left1, right1, k); // 保证 len1 不大于 len2
if(len1==0) return nums2[left2+k-1]; // 如果 len1==0，直接返回当前 nums2 的第 k 个元素
if(k==1) return min(nums1[left1], nums2[left2]); // 如果 k==1，则返回两个数组头更小的那个元素
int i = left1 + min(k/2, len1)-1; // 第 k/2 个元素，为了防止数组长度小于 k/2，用了 min 函数
int j = left2 + min(k/2, len2)-1; // 同上
if(nums1[i]<nums2[j])
return find(nums1, i+1, right1, nums2, left2, right2, k-(i-left1+1)); // 别忘了最后一个参数
else
return find(nums1, left1, right1, nums2, j+1, right2, k-(j-left2+1));
}
};
代码中还有一点，就是我们同时计算了第 left 小的元素和第 right 小的元素，然后求两者的平均值作为答案。这样做的原因是，假设两个数组长度分别为 len1 和 len2，如果 len1+len2 为偶数，则我们需要求中间两个数的平均值，中间两个数就是第 left 小的元素和第 right 小的元素；如果 len1+len2 为奇数，则中间的那个数就是中位数，这时第 left 小的元素和第 right 小的元素是一样的，会发生重复计算。
