【LeetCode-数学】剪绳子
题目描述
给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。
示例：
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
说明：
- 2 <= n <= 58；
- 该题是《剑指Offer》的第 14 题；
题目链接： https://leetcode-cn.com/problems/jian-sheng-zi-lcof/
思路
将长度为 n 的绳子分成 a 段：
\[n = n_1 + n_2+n_3+\dots+n_a
\]
使得，每段长度的乘积最大：
\[max(n_1 \times n_2 \times n_3 \times \dots \times n_a)
\]
因为
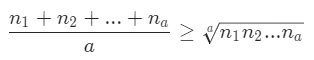
上面的不等式当 \(n_1=n_2=\dots=n_a\) 时等式成立，也就是说均分长度为 n 的绳子时，得到的乘积最大。均分多少段才能得到最大值呢？假设均分为 a 段，每段的长度为 x，也就是 \(n = ax\)，那么每一段的乘积为：
\[x^a = x^{\frac{n}{x}} = (x^{\frac{1}{x}})^n
\]
因为 n 是确定的，所以最大化 \((x^{\frac{1}{x}})^n\)，就等于最大化 $ x^{\frac{1}{x}} $，我们对 \(x^{\frac{1}{x}}\) 取对数得到 \(\frac{1}{x} \ln x\)，最大化 \(x^{\frac{1}{x}}\) 就等于最大化 \(\frac{1}{x} \ln x\)，我们对 \(\frac{1}{x} \ln x\) 求导可得：
\[\frac{1}{x^2} - \frac{1}{x^2} \ln x \\
= \frac{1- \ln x}{x^2}
\]
令上式为 0，可以得到 \(1-\ln x=0\)，所以 x = e = 2.7.....，由于每段的长度 x 必须为整数，所以 x 为 2 或者 3 比较好。因为 \(3^{\frac{1}{3}}>2^{\frac{1}{2}}\)，所以每段的长度为 3 最好。
我们可以得出以下结论：
- 最优长度：3。把绳子尽可能切为多个长度为 3 的片段，留下的最后一段绳子的长度可能为 0，1，2 三种情况。
- 次优长度：2。若最后一段绳子长度为 2 ；则保留，不再拆为 1 + 1。
- 最差长度：1。若最后一段绳子长度为 1 ；则应把一份 3 + 1 替换为 2 + 2，因为 2 x 2 > 3 x 1。
所以算法如下：
- 如果绳子的长度 n 小于等于 3，因为必须要对绳子进行切分，所以我们将绳子分为 n-1 和 1 两部分，返回 n-1；
- a = n/3，b = n%3，表示 n 能切分成 a 段长度为 3 的绳子，并且最后一段绳子的长度为 b；
- 如果 b==0，表示 n 能被 3 整除，返回 \(3^a\)；
- 如果 b==1，说明最后一段的长度为 1，则要将 3 + 1 转换为 2 + 2，所以返回 \(3^{a-1}*4\)；
- 如果 b==2，说明最后一段的长度为 2，则返回 \(3^a*2\)；
代码如下：
class Solution {
public:
int cuttingRope(int n) {
if(n<=3) return n-1;
int a = n / 3;
int b = n % 3;
if(b==0) return pow(3, a);
if(b==1) return pow(3, a-1) * 4;
if(b==2) return pow(3, a) * 2;
return 0; // 不会运行到这一步
}
};
- 时间复杂度：O(1)
- 空间复杂度：O(1)
