【深度学习】常用优化器总结

在训练模型时，我们可以基于梯度使用不同的优化器（optimizer，或者称为“优化算法”）来最小化损失函数。这篇文章对常用的优化器进行了总结。

BGD

BGD 的全称是 Batch Gradient Descent，中文名称是批量梯度下降。顾名思义，BGD 根据整个训练集计算梯度进行梯度下降

\[\theta = \theta - \eta\Delta_{\theta}J(\theta) \]

其中，\(J(\theta)\) 是根据整个训练集计算出来的损失。

• 优点
  • 当损失函数是凸函数（convex）时，BGD 能收敛到全局最优；当损失函数非凸（non-convex）时，BGD 能收敛到局部最优；
• 缺点
  • 每次都要根据全部的数据来计算梯度，速度会比较慢；
  • BGD 不能够在线训练，也就是不能根据新数据来实时更新模型；

SGD

SGD 的全称是 Stochastic Gradient Descent，中文名称是随机梯度下降。和 BGD 相反，SGD 每次只使用一个训练样本来进行梯度更新：

\[\theta = \theta - \eta\Delta_{\theta}J(\theta;x^{(i)};y^{(i)}) \]

其中，\(J(\theta;x^{(i)};y^{(i)})\) 是只根据样本 \((x^{(i)};y^{(i)})\) 计算出的损失。

• 优点
  • SGD 每次只根据一个样本计算梯度，速度较快；
  • SGD 可以根据新样本实时地更新模型；
• 缺点
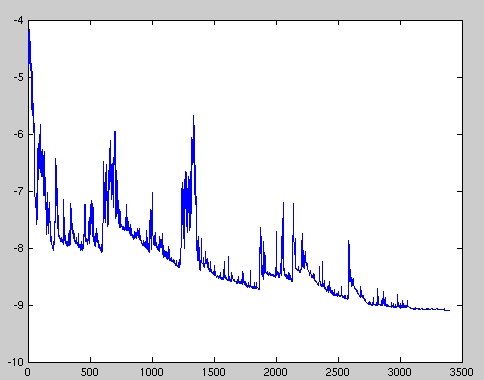
  • SGD 在优化的过程中损失的震荡会比较严重；
    

MBGD

MBGD 的全称是 Mini-batch Gradient Descent，中文名称是小批量梯度下降。MBGD 是 BGD 和 SGD 的折中。MBGD 每次使用包含 m 个样本的小批量数据来计算梯度

\[\theta = \theta - \eta\Delta_{\theta}J(\theta;x^{(i:i+m)};y^{(i:i+m)}) \]

其中，\(m\) 为小批量的大小，范围是 \([1, n]\)，\(n\) 为训练集的大小；\(J(\theta;x^{(i:i+m)};y^{(i:i+m)})\) 是根据第 \(i\) 个样本到第 \(i+m\) 个样本计算出来的损失。
当 \(m==1\) 时，MBGD 变为 SGD；当 \(m==n\) 时，MBGD 变为 BGD。

• 优点
  • 收敛更加稳定；
  • 可以利用高度优化的矩阵库来加速计算过程；
• 缺点
  • 选择一个合适的学习率比较困难；
  • 相同的学习率被应用到了所有的参数，我们希望对出现频率低的特征进行大一点的更新，所以我们希望对不同的参数应用不同的学习率；
  • 容易被困在鞍点（saddle point）；
    

上图的红点就是一个鞍点。上面 MBGD 的 3 个缺点也可以说是 SGD 和 BGD 的 3 个缺点。为了解决这 3 个缺点，研究人员提出了 Momentum、Adagrad、RMSprop、Adadelta、Adam 等优化器。在这介绍这些优化器之前，需要介绍一下指数加权平均（Exponentially Weighted Sum），因为这些改进的优化器或多或少都用了它。

指数加权平均

假设用 \(\theta_t\) 表示一年中第 \(t\) 天的温度，\(t\in[1,365]\)。我们以天为横轴，以温度为纵轴，可以得到下图

如果我们想要获得这些数据的局部平均或滑动平均，我们可以设置一个变量 \(v_t\)，\(v_t\) 的计算方法如下

\[v_t = \beta v_{t-1} + (1-\beta)\theta_t, t>1 \]

当 \(t==1\) 时，我们令 \(v_t=0\)。这样，\(v_t\) 就约等于第 t 天之前 \(\frac{1}{1-\beta}\) 天的平均温度（局部平均）。例如，当 \(\beta=0.9\) 时，\(v_t\) 就约等于第 \(t\) 天前 \(\frac{1}{1-0.9}=10\) 天的平均温度。我们计算出 \(v_t\) 可以得到下图中的红色曲线

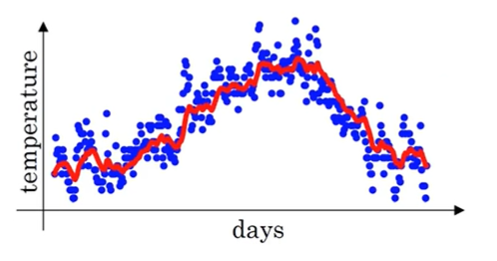
可以看到，\(v_t\) 对原始数据做了平滑，降低了原始数据的震荡程度。
当我们将 \(\beta\) 设为 0.98 并计算 \(v_t\)，可以得到下图中的绿色曲线

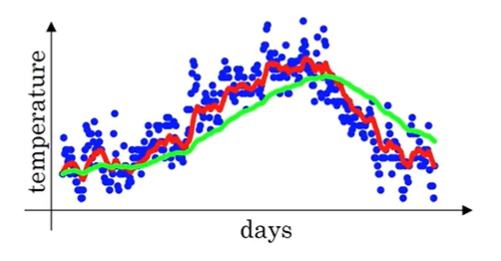
偏差修正

当我们将 \(\beta\) 设为 0.98 并使用公式 \(v_t = \beta v_{t-1} + (1-\beta)\theta_t\) 计算 \(v_t\) 并将其画在坐标系中，我们得到的其实不是上图中的绿色曲线，而是下图中的紫色曲线

可以看到，紫色曲线在后半段和蓝色曲线是重合的，前半段有一些偏差，而且紫色曲线的刚开始时非常接近于 0 的，原因是我们设置 \(v_1=0\)，所以刚开始的 \(v_t\) 会比较接近 0，也就不能代表前 \(\frac{1}{1-\beta}\) 天的平均温度。为了修正这个偏差，我们对 \(v_t\) 将缩放为 \(\frac{v_t}{1-\beta^t}\)，这样 t 比较小时分母会是一个小于 1 的小数，能对 \(v_t\) 进行放大；随着 \(t\) 的增大，分母会越来越接近 1，\(\frac{v_t}{1-\beta^t}\) 也就变成了 \(v_t\)。所以上图中，紫色曲线和绿色曲线在后半段重合。

指数加权平均减小了原始数据的震荡程度，能对原始数据起到平滑的效果。

Momentum

假设模型在时间 \(t\) 的梯度为 \(\Delta J(\theta)\)，则 Momentum 的梯度更新方法如下

\[v_t = \beta v_{t-1} + (1-\beta) \Delta J(\theta) \\ \theta = \theta - \alpha v_t \]

其中，\(v_t\) 就是模型前 \(\frac{1}{1-\beta}\) 步梯度的平均值，\(\beta\) 通常设为 0.9，\(\alpha\) 为学习率。

也可以换一种写法，就是将 \((1-\beta)\) 这一项去掉

\[v_t = \beta v_{t-1} + \alpha \Delta J(\theta) \\ \theta = \theta - v_t \]

第一种写法更容易理解，所以下面的公式都采用第一种写法。

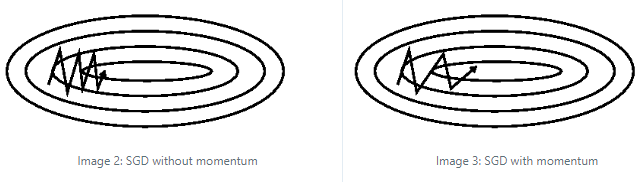
在上图中，左图是不使用 Momentum 的 SGD，而右图是使用 Momentum 的 SGD。可以看到，Momentum 通过对前面一部分梯度的指数加权平均使得梯度下降的过程更加平滑，减少了震荡，收敛也比普通的 SGD 更快。

NAG

NAG（Nesterov Accelerated Gradient） 对 Momentum 进行了轻微的修改

\[v_t = \beta v_{t-1} + (1-\beta) \Delta J(\theta-\beta v_{t-1}) \\ \theta = \theta - \alpha v_t \]

也就是，在进行梯度更新前，我们先看一下 Momentum 指向的位置，然后在 Momentum 指向的位置计算梯度并进行更新。如下图

有很多优化器的名称中包含 Ada ，Ada 的含义是 Adaptive，代表“自适应性的”。名称中带有 Ada 的优化器一般意味着能够自动适应（调节）参数的学习率。

Adagrad

在我们训练模型的初期我们的学习率一般比较大，因为这时我们的位置离最优点比较远；当训练快结束时，我们通常会降低学习率，因为训练快结束时我们离最优点比较近，这时使用大的学习率可能会跳过最优点。Adagrad 能使得参数的学习率在训练的过程中越来越小，具体计算方法如下：

\[\theta = \theta - \frac{\eta}{\sqrt{\sum_tg_t^2+\epsilon}}g_t \]

其中，\(g_t\) 是模型在 \(t\) 时刻的梯度，\(\sum_tg_t^2\) 是模型前 t 个时刻梯度的平方和，\(\epsilon\) 防止分母为 0，一般将 \(\epsilon\) 设为一个很小的数，例如 \(10^{-8}\)。在训练的过程中，\(\sqrt{\sum_tg_t^2+\epsilon}\) 会越来越大，\(\frac{\eta}{\sqrt{\sum_tg_t^2+\epsilon}}\) 会越来越小，所以学习率也会越来越小。\(\eta\) 通常设为 0.01。

• 优点
  • 自动调节参数的学习率；
• 缺点
  • 学习率下降会比较快，可能造成学习提早停止；

Adadelta

Adadelta 对 Adagrad 做了轻微的修改，使其比 Adagrad 更加稳定。Adadelta 的计算方法如下：

\[\theta = \theta - \frac{\eta}{\sqrt{E[g^2]_t+\epsilon}}g_t \\ E[g_t^2] = \beta E[g^2]_{t-1} + (1-\beta) g_{t-1}^2 \]

其中，\(E[g^2]_t\) 表示前 \(t\) 个梯度平方和的期望，也就是梯度平方和的指数加权平均。Adadelta 把 Adagrad 分母中的梯度平方和换成了梯度平方的指数加权平均，这使得 Adadelta 学习率的下降速度没有 Adagrad 那么快。

RMSprop

RMSprop 的全称是 Root Mean Squre propogation，也就是均方根（反向）传播。RMSprop 可以看做是 Adadelta 的一个特例

\[E[g^2]_t = \beta E[g^2]_{t-1} + (1-\beta) g_{t-1}^2 \]

Adadelta 中使用了上式来计算 \(E[g_t^2]\)。当参数 \(\beta=0.5\) 时，\(E[g_t^2]\) 就变成了梯度平方和的平均数，再求根的话，就变成了 RMS，也就是

\[RMS[g]_t = \sqrt{E[g^2]_t+\epsilon} \]

RMSprop 中参数的更新方法为

\[\theta = \theta - \frac{\eta}{RMS[g]_t}g_t \\ \]

Adam

Adam 的全称是 Adaptive Moment Estimation，其可看作是 Momentum + RMSprop。Adam 使用梯度的指数加权平均（一阶矩估计）和梯度平方的指数加权平均（二阶矩估计）来动态地调整每个参数的学习率。

\[m_t = \beta m_{t-1} + (1-\beta) g_t \\ n_t = \gamma n_{t-1} + (1-\gamma) g_t^2 \]

其中，\(m_t、n_t\) 分别是梯度的指数加权平均（一阶矩估计）和梯度平方的指数加权平均（二阶矩估计）。然后，对\(m_t\) 和 \(n_t\) 进行偏差修正

\[\hat m_t = \frac{m_t}{1-\beta^t} \\ \hat n_t = \frac{n_t}{1-\gamma^t} \]

\(m_t、n_t\) 分别是梯度的一阶矩估计和二阶矩估计，可以看做是对期望 \(E[g]_t\) 和 \(E[g^2]_t\) 的估计。通过偏差修正，\(\hat m_t\) 和 \(\hat n_t\) 可以看做是为期望的无偏估计。最后，梯度的更新方法为

\[\theta = \theta - \frac{\eta}{\sqrt{\hat n_t}+\epsilon} \hat m_t \]

在使用中，\(\beta\) 通常设为 0.9，\(\gamma\) 通常设为 0.999，\(\epsilon\) 通常设为 \(10^{-8}\)。

参考

1、ruder.io/optimizing-gradient-descent/
2、towardsdatascience.com/stochastic-gradient-descent-with-momentum-a84097641a5d
3、akyrillidis.github.io/notes/AdaDelta
4、zhuanlan.zhihu.com/p/22252270
5、jiqizhixin.com/graph/technologies/173c1ba6-0a13-45f6-9374-ec0389124832
6、https://www.cnblogs.com/guoyaohua/p/8542554.html
7、吴恩达《深度学习》课程：https://www.bilibili.com/video/BV1gb411j7Bs?p=60