【LeetCode-树】把二叉搜索树转换为累加树

题目描述

给定一个二叉搜索树（Binary Search Tree），把它转换成为累加树（Greater Tree)，使得每个节点的值是原来的节点值加上所有大于它的节点值之和。
示例：

输入: 原始二叉搜索树:
              5
            /   \
           2     13

输出: 转换为累加树:
             18
            /   \
          20     13

题目链接： https://leetcode-cn.com/problems/convert-bst-to-greater-tree/

思路1

首先递归得到二叉树中节点的值序列 v，然后再遍历一遍二叉树，当遍历当前节点时，假如当前节点的值为 val，则遍历值序列，如果值 v[i] 大于 val，则 val+=v[i]，然后拿 val 更新节点的值。代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* convertBST(TreeNode* root) {
        if(root==nullptr) return nullptr;

        vector<int> v;
        inOrder(root, v); // 得到节点值序列存在 v 中

        return dfs(root, v); 
    }

    void inOrder(TreeNode* root, vector<int>& v){
        if(root==nullptr) return;

        inOrder(root->left, v);
        v.push_back(root->val);
        inOrder(root->right, v);
    }

    TreeNode* dfs(TreeNode* root, vector<int> v){
        if(root==nullptr) return nullptr;

        int val = root->val;
        int temp = val;
        for(int i=0; i<v.size(); i++){
            if(v[i]>temp) val+=v[i];
        }
        root->val = val;
        root->left = dfs(root->left, v);
        root->right = dfs(root->right, v);
        return root;
    }
};

• 时间复杂度：O(n^2)
  n 为树中的节点个数。
• 空间复杂度：O(h)
  h 为树高。

思路2

思路1中并没有用到输入的树是二叉搜索树这个性质。二叉搜索树的中序遍历序列是一个递增序列。

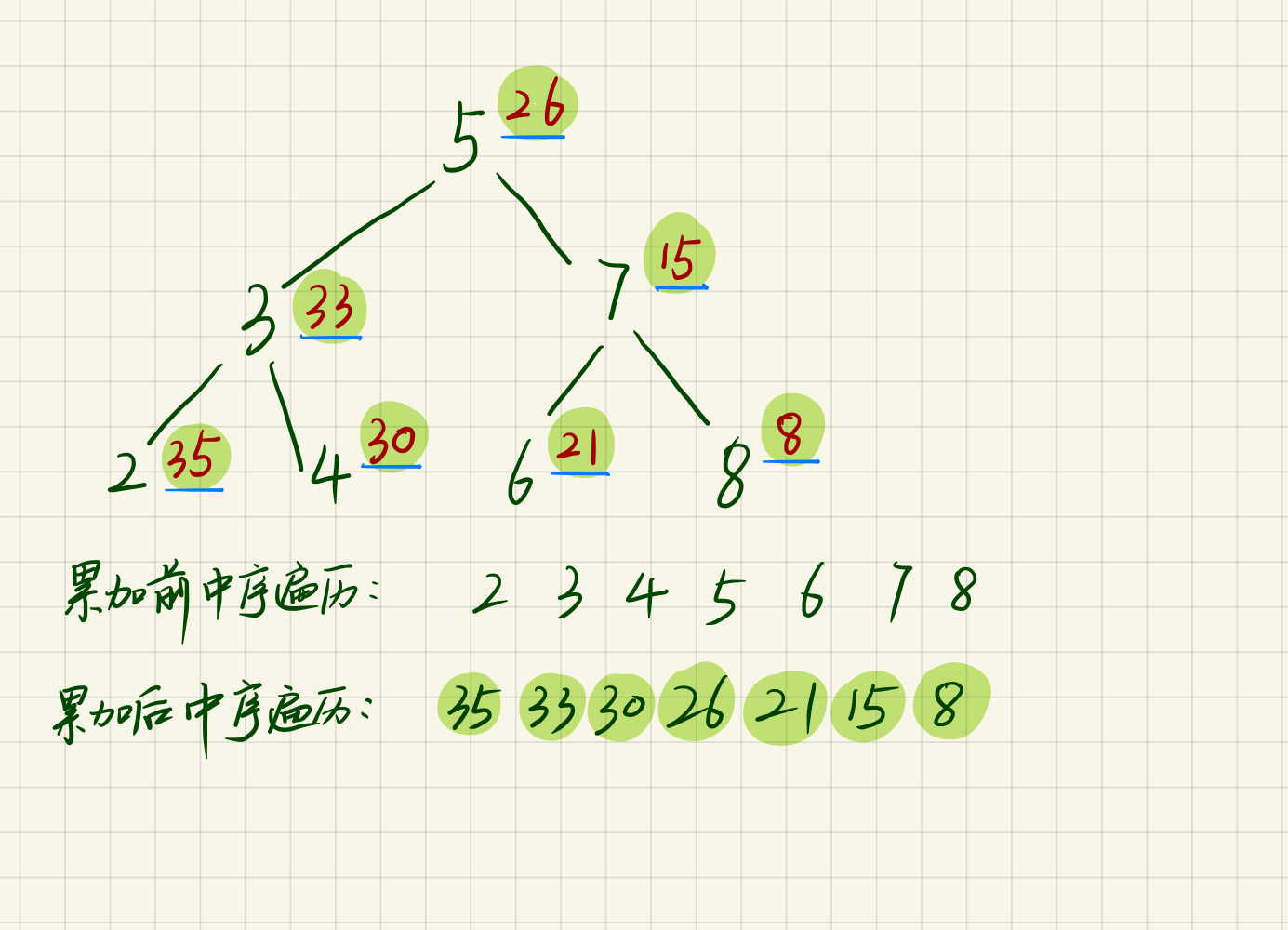
图来自这篇题解。从上图可以看到，累加后的序列就是累加前的序列从后往前累加的结果。所以，我们可以使用“右中左”（反向中序遍历）来遍历二叉树实现向后累加。代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* convertBST(TreeNode* root) {
        if(root==nullptr) return root;

        int sum = 0;
        inOrder(root, sum);
        return root;
    }

    void inOrder(TreeNode* root, int& sum){
        if(root==nullptr) return;

        inOrder(root->right, sum);
        sum += root->val;
        root->val = sum;
        inOrder(root->left, sum);
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(h)