【机器学习】激活函数总结

饱和性

左饱和和右饱和

我们定义\(y=f(x)\)，其中，\(x\) 为激活函数输入值，\(f(\cdot)\) 为激活函数，\(y\) 为激活函数的输出值。激活函数的饱和性通过导数来判断，具体如下：

• 如果 \(x\rightarrow +\inf\) 时，\(f'(x)=0\)，我们说激活函数 \(f(x)\) 右饱和；
• 如果 \(x\rightarrow -\inf\) 时，\(f'(x)=0\)，我们说激活函数 \(f(x)\) 左饱和；
• 如果 \(f(x)\) 即是左饱和的，又是右饱和的，我们说 \(f(x)\) 饱和（软饱和），例如 sigmoid 函数就是饱和的。

硬饱和和软饱和

根据 \(f'(x)\) 趋向于 0 的位置，饱和又可以分为硬饱和和软饱和。

• 如果\(x\rightarrow +c\) 时, \(f'(x)=0\)，我们说激活函数 \(f(x)\) 右硬饱和；
• 如果\(x\rightarrow -c\) 时，\(f'(x)=0\)，我们说激活函数 \(f(x)\) 左硬饱和；
• 如果 \(f(x)\) 即是左硬饱和的，又是右硬饱和的，我们说 \(f(x)\) 硬饱和。

如果 \(c=\inf\) 并满足上面的三个条件（也就退化成了第一节的三个条件），那么 \(f(x)\) 软饱和。

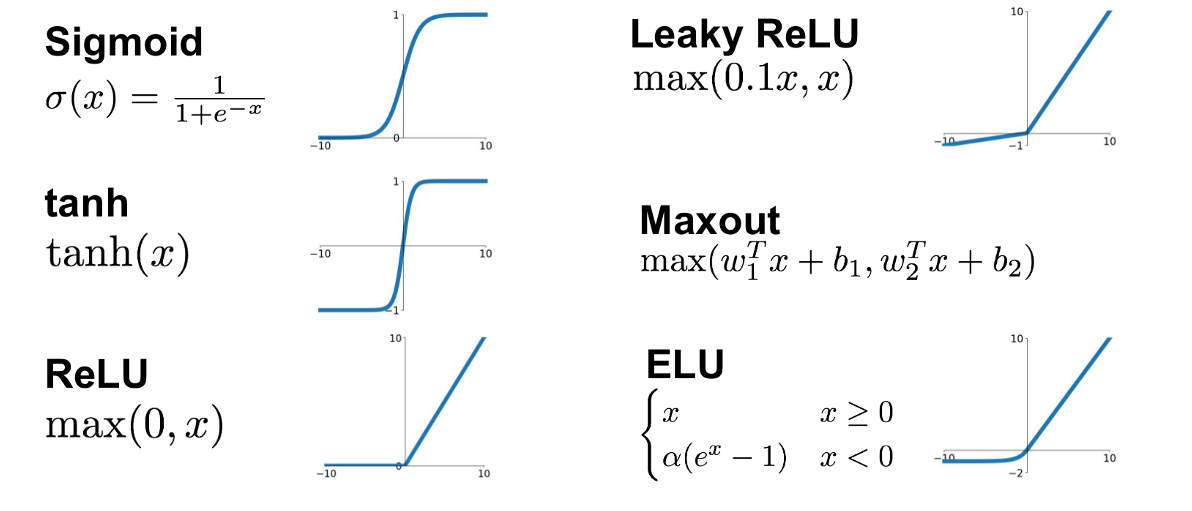
Sigmoid

Sigmoid 的含义是“S 型函数”，其表示如下：

\[\sigma(z) = \frac{1}{1+e^{-z}} \]

函数图像如下：

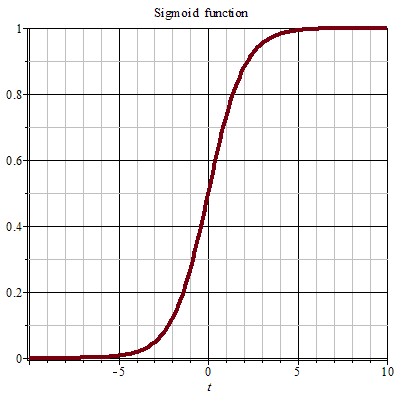
优点

• 输出值位于[0, 1]之间，适合表示概率；
• 易于求导，因为 \(\sigma^{\prime} = \sigma(x)(1-\sigma(x))\)；

缺点

• Sigmoid 函数容易饱和，其梯度范围为 (0, 0.25]，容易产生梯度消失问题；
• 输出不以 0 为中心，输出全为正值，会导致模型收敛速度变慢；
• 相对于有些激活函数计算成本高昂，因为牵扯到指数运算。

Tanh

Tanh 的表示如下：

\[tanh(z) = 2\sigma(2z)-1=\frac{e^{2z}-1}{e^{2z}+1} \]

其函数图像如下：

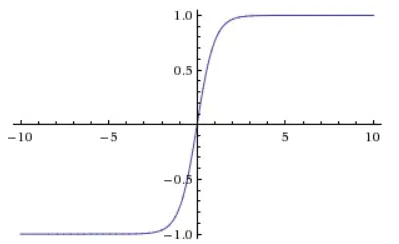
优点

• 函数以 0 为中心，输出包含负值，收敛速度会比 sigmoid 更快；

缺点

• 和 sigmoid 一样，tanh 也是饱和激活函数，容易出现梯度消失的问题；

ReLU

ReLU（Rectified Linear Unit， 线性修正单元）的表示如下：

\[relu(z) = max(0, z) \]

图像如下：

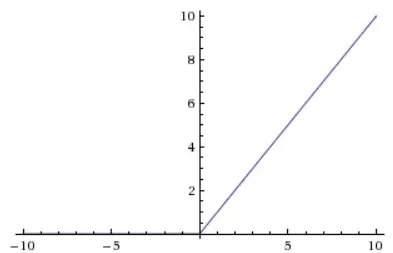
优点

• ReLU 的导数非常简单，不会涉及求指数操作，实现起来较为简单；
• ReLU 有效缓解了梯度消失的问题；
• 相比较于 sigmoid 和 tanh，ReLU 能更快收敛；
• ReLU 提供了神经网络稀疏表达的能力。

缺点

• 训练过程中会出现神经元死亡的问题。如果在某一次不恰当的更新后，偏置 b 变成了一个非常大的负数，那么 ReLU 的输入将会是一个负数。对于负数输入，ReLU 的输出为 0，导数也为 0，所以该神经元得不到更新，从而“死亡”。

Leaky-ReLU

为了解决 ReLU 可能导致神经元出现死亡的问题，Leaky-ReLU 被提出。Leaky-ReLU 的表达式如下：

\[\text{Leaky-ReLU}(z)=\left\{ \begin{aligned} z,~~ z\ge 0 \\ \alpha z,~~ z < 0 \end{aligned} \right. \]

函数图像如下：

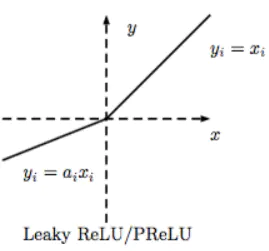
优点

• 类似 ELU，Leaky ReLU 也能避免死亡 ReLU 问题，因为其在计算导数时允许较小的梯度；
• 由于不包含指数运算，所以计算速度比 ELU 快。

缺点

• 无法避免梯度爆炸问题；
• 神经网络不学习 α 值；
• 在微分时，两部分都是线性的；而 ELU 的一部分是线性的，一部分是非线性的。

ELU

ELU（Exponential Linear Unit，指数线性单元）和 Leaky-ReLU 很像。Leaky-ReLU 在输入小于 0 时是一个线性函数，而 ELU 在输入小于 0 时是一个指数函数。ELU 的定义如下：

\[\text{ELU}(z)=\left\{ \begin{array}{l} z,~~ z\ge 0 \\ \alpha \cdot (e^z-1) z,~~ z < 0 \end{array} \right. \]

函数图像如下：

优点

• 能避免死亡 ReLU 问题；
• 能得到负值输出，这能帮助网络向正确的方向推动权重和偏置变化；
• 在计算梯度时能得到激活，而不是让它们等于 0。

缺点

• 由于包含指数运算，所以计算时间更长；
• 无法避免梯度爆炸问题；
• 神经网络不学习 α 值。

Maxout

Maxout 的定义如下：

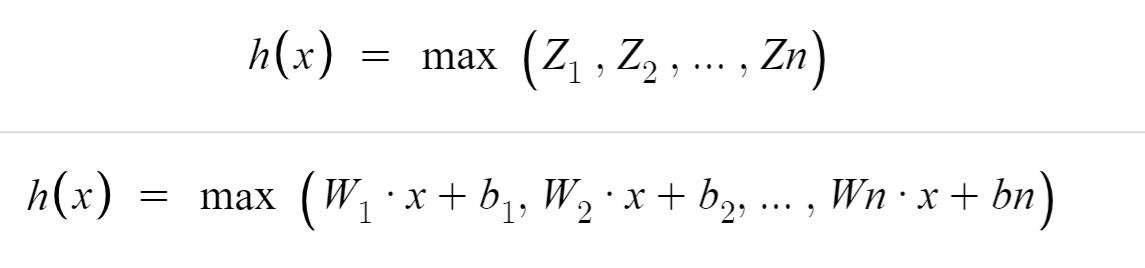
也就是，Maxout 将输入通过 n 个不同的线性单元，取最大值作为 Maxout 的输出值。

优点

• 同时具备 ReLU 和 Leaky-ReLU 的优点；

缺点

• 参数变多；

总结

参考

1、jianshu.com/p/71819140ca11
2、https://sefiks.com/2018/01/02/elu-as-a-neural-networks-activation-function/
3、https://towardsdatascience.com/complete-guide-of-activation-functions-34076e95d044
4、ml-cheatsheet.readthedocs.io/en/latest/activation_functions.html#elu
5、zhuanlan.zhihu.com/p/98863801