【LeetCode-数组】接雨水
题目描述
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。 感谢 Marcos 贡献此图。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
题目链接: https://leetcode-cn.com/problems/trapping-rain-water/
思路1
按列来做。每一个柱子上面可以存储的水的容量由该柱子左右两边最长的柱子之间最短的那个柱子决定。例如,
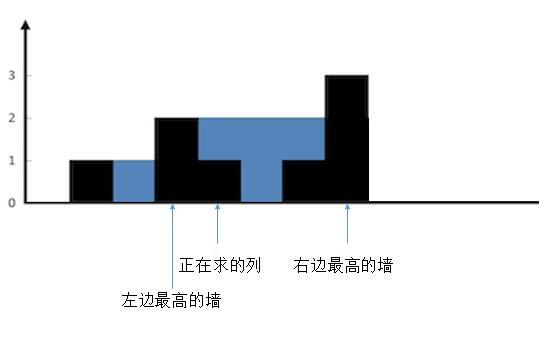
我们当前的柱子的高度为 height[i]=1,height[i] 左边最高的柱子的高度为 2,height[i] 右边最高的柱子的高度为 3,两者之间的较小值为 2,而当前柱子的高度为 1,则当前柱子上能存储 2-1 = 1 个单位的水,这是当前柱子的高度小于等于左右两个柱子之间较小值的情况。如果较小值小于当前柱子的高度,水会漏掉,所以当前柱子上不能存储水,则就是存储水的单位为 0,如下所示:
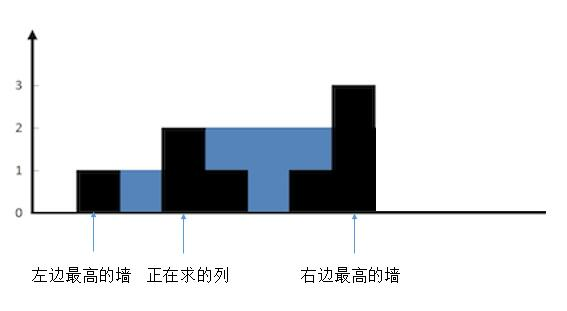
由于第一个柱子和最后一个柱子位于边界,不会存储水,所以遍历时从第一个柱子开始,到倒数第二个柱子结束。
所以算法如下:
- 遍历 height:
- 计算当前柱子左边最高的柱子的高度 leftMax;
- 计算当前柱子右边最高的柱子的高度 rightMax;
- 计算 leftMax 和 rightMax 的较小者,记为 minHeight;
- 如果 minHeight>当前柱子的高度 height[i],则将 minHeight-height[i] 加入到答案中。
代码如下:
class Solution {
public:
int trap(vector<int>& height) {
if(height.empty()) return 0;
int ans = 0;
for(int i=1; i<height.size()-1; i++){
int leftMax = 0;
for(int j=0; j<i; j++){
if(height[j]>leftMax) leftMax = height[j];
}
int rightMax = 0;
for(int j=i+1; j<height.size(); j++){
if(height[j]>rightMax) rightMax = height[j];
}
int minHeight = min(leftMax, rightMax);
if(minHeight>height[i]) ans += (minHeight - height[i]);
}
return ans;
}
};
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
思路2
思路 1 有一个缺点,就是每次都要从当前元素分别向左右遍历来寻找左边和右边的最大高度,这增加了时间复杂度。可以用 leftMax[i] 和 rightMax[i] 分别表示 height[i] 左边和右边的最大高度。我们提前通过动态规划计算好这两个数组。以 leftMax[] 为例:
- 状态定义:leftMax[i] 表示 height[i] 左边的最高柱子的高度;
- 递推公式:leftMax[i] = max(height[i], leftMax[i-1]),从左往右推;
- 边界条件:leftMax[0] = height[0];
其他步骤和思路 1 一致,代码如下:
class Solution {
public:
int trap(vector<int>& height) {
if(height.empty()) return 0;
vector<int> leftMax(height.size(), 0);
for(int i=0; i<height.size(); i++){
if(i==0) leftMax[i] = height[i];
else leftMax[i] = max(height[i], leftMax[i-1]);
}
vector<int> rightMax(height.size(), 0);
for(int i=height.size()-1; i>=0; i--){
if(i==height.size()-1) rightMax[i] = height[i];
else rightMax[i] = max(height[i], rightMax[i+1]);
}
int ans = 0;
for(int i=1; i<height.size()-1; i++){
int minHeight = min(leftMax[i], rightMax[i]);
if(minHeight>height[i]) ans += (minHeight-height[i]);
}
return ans;
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
思路3
使用单调栈来做,具体是单调递减栈。单调递减栈中的元素从栈底到栈顶依次递减。因为要计算宽度,所以栈中存储的是下标,而不是高度。
- 遍历数组:
- 如果栈不空并且当前元素大于栈顶元素,则计算储水单位;
- 否则,将当前下标入栈。
具体细节如下:
class Solution {
public:
int trap(vector<int>& height) {
if(height.empty()) return {};
int ans = 0;
stack<int> s;
for(int i=0; i<height.size(); i++){
while(!s.empty() && height[s.top()]<height[i]){
int cur = s.top(); s.pop();
if(s.empty()) break;
int left = s.top();
int right = i;
int minHeight = min(height[left], height[right]) - height[cur];
ans += (right-left-1)*minHeight;
}
s.push(i);
}
return ans;
}
};
个人觉得单调栈不是很好写,很容易出错。
- 时间复杂度:O(n)
- 空间复杂度:O(n)
思路4
使用类似于韦恩图的方法来做。首先从左到右计算面积,记为 leftArea:
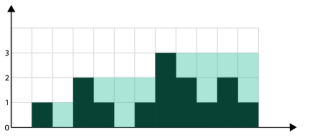
然后从右到左计算面积,记为 rightArea:

这样,leftArea + rightArea 会覆盖整个矩形:

在上图中,柱子以及阴影部分都被计算了两次,所以有,leftArea + rightArea = 粉色面积 + 绿色面积 + 柱子面积 + 阴影面积 + 柱子面积 + 阴影面积 = 矩形面积 + 柱子面积 + 阴影面积(前面四项合并)。所以,阴影面积 = leftArea + rightArea - 矩形面积 - 柱子面积。
代码如下:
class Solution {
public:
int trap(vector<int>& height) {
if(height.empty()) return {};
int leftArea = 0;
int curLeftMax = 0;
for(int i=0; i<height.size(); i++){
curLeftMax = max(height[i], curLeftMax);
leftArea += curLeftMax;
}
int rightArea = 0;
int curRightMax = 0;
for(int i=height.size()-1; i>=0; i--){
curRightMax = max(height[i], curRightMax);
rightArea += curRightMax;
}
int pillarArea = 0; // 柱子面积
for(int i=0; i<height.size(); i++){
pillarArea += height[i];
}
return leftArea + rightArea - pillarArea - height.size() * curLeftMax;
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
参考
1、思路1、思路2:https://leetcode-cn.com/problems/trapping-rain-water/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-w-8/
2、思路3:https://leetcode-cn.com/problems/trapping-rain-water/solution/trapping-rain-water-by-ikaruga/
3、思路4:https://leetcode-cn.com/problems/trapping-rain-water/solution/wei-en-tu-jie-fa-zui-jian-dan-yi-dong-10xing-jie-j/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号