【LeetCode-设计】LRU缓存机制
题目描述
运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作: 获取数据 get 和 写入数据 put 。
获取数据 get(key) - 如果密钥 (key) 存在于缓存中,则获取密钥的值(总是正数),否则返回 -1。
写入数据 put(key, value) - 如果密钥已经存在,则变更其数据值;如果密钥不存在,则插入该组「密钥/数据值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
进阶:
你是否可以在 O(1) 时间复杂度内完成这两种操作?
示例:
LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );
cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // 返回 1
cache.put(3, 3); // 该操作会使得密钥 2 作废
cache.get(2); // 返回 -1 (未找到)
cache.put(4, 4); // 该操作会使得密钥 1 作废
cache.get(1); // 返回 -1 (未找到)
cache.get(3); // 返回 3
cache.get(4); // 返回 4
题目链接: https://leetcode-cn.com/problems/lru-cache/
思路
题目要求在 O(1) 的时间进行查找和插入,那我们的缓存 cache 也应该是有序的:cache 头是最近访问的,cache 尾是最久未被访问的。我们可以使用哈希表来进行 O(1) 时间复杂度的查找,但是哈希表不满足有序这个条件,所以我们需要一种新的数据结构:哈希链表。
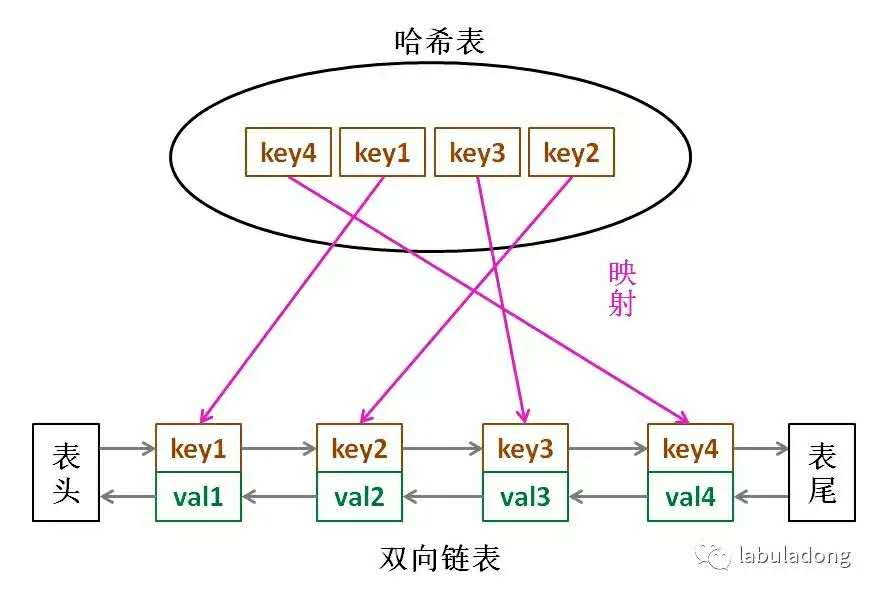
哈希表的 key 就是输入的 key,value 是 key 对应的链表节点,链表节点包含 2 个字段: key 和 value。哈希表和链表的定义如下:
list<pair<int, int>> cache; // STL 中的 list 为双向链表
unordered_map<int, list<pair<int, int>>::iterator> hash;
查找:
- 在哈希表中寻找键为 key 的元素,如果存在,则返回 key 对应链表节点当中的 value,并将该节点提到链表头,表示刚刚访问过,并更新哈希表中 key 对应的 value;
- 如果不存在,则返回 -1;
插入:
- 查看要插入的 key 在哈希表中是否存在:
- 如果存在,则在链表中找到 key 对应的链表节点,更新节点中的 value 字段,并将该节点提到链表头,然后更新哈希表中 key 对应的 value;
- 如果不存在,则说明是新插入的元素,则判断当前元素个数是否小于缓存 cache 的容量:
- 如果小于,则直接将新元素的 key 和 value 插入到链表头,在哈希表中添加 key;
- 如果不小于,则需要删除最久未使用的元素,最久未使用的元素就是链表尾的元素,所以将链表尾的元素删除,在哈希表中将对应的 key 删除,然后将新的 key 和 value 插入到链表头,在哈希表中添加 key;
两个疑问:
- 为什么使用双向链表?
- 因为双向链表才能保证删除元素的时间复杂度为 O(1).
- 哈希表中已经有 key 了,链表节点中为什么还存储 key?
- 因为当我们删除链表中的节点时,也要把该节点对应的 key 在哈希表中删除,如果链表节点不存储 key 的话,我们就不知道在哈希表中删除哪个值了。
class LRUCache {
list<pair<int, int>> cache;
unordered_map<int, list<pair<int, int>>::iterator> hash;
int capacity;
public:
LRUCache(int capacity) {
this->capacity = capacity;
}
int get(int key) {
if(hash.find(key)!=hash.end()){
pair<int, int> kv = *hash[key];
/*int key = kv.first;
int value = kv.second;*/
cache.erase(hash[key]);
cache.push_front(kv);
hash[key] = cache.begin();
return kv.second;
} else return -1;
}
void put(int key, int value) {
auto it = hash.find(key);
if(it!=hash.end()){
pair<int, int> kv = *hash[key];
/*int key = kv.first;
int value = kv.second;*/
cache.erase(hash[key]);
cache.push_front(make_pair(key, value));
hash[key] = cache.begin();
}else{
if(cache.size()<capacity){
cache.push_front(make_pair(key, value));
hash[key] = cache.begin();
}else{
auto last = cache.back();
int lastKey = last.first;
cache.pop_back();
hash.erase(lastKey);
cache.push_front(make_pair(key, value));
hash[key] = cache.begin();
}
}
}
};
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache* obj = new LRUCache(capacity);
* int param_1 = obj->get(key);
* obj->put(key,value);
*/
注意,get 不能这么写:
int get(int key) {
if(hash.count(key)!=0){
auto pr = hash[key];
cache.erase(pr);
cache.push_front(*pr);
hash[key] = cache.begin();
return pr->second;
}else return -1;
}
这样写会报错。
- 时间复杂度:O(1)
- 空间复杂度:O(capacity)
参考
1、https://leetcode-cn.com/problems/lru-cache/solution/lru-ce-lue-xiang-jie-he-shi-xian-by-labuladong/ ,这篇题解写的挺好的,上面的图也是来自于这篇题解。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号