【机器学习】线性模型

这篇文章总结了 3 种线性模型：线性回归、对数线性回归和逻辑斯蒂回归（logistic regression，LR，对数几率回归）。

线性回归

假设数据集 \(D=\{(x_1, y_1), (x_2, y_2),\dots,(x_m,y_m)\}\)，其中 \(x_i = (x_{i1};x_{i_2};\dots;x_{id})\)，\(y \in R\)。 也就是，数据集 \(D\) 共包含 m 个样本，每个样本含有 d 个属性. 线性回归的目标是找到参数 \(w = (w_1, w_2, \dots, w_m)\) 和 \(b\)，使得

\[f(x_i) = w_1x_{i1} + w_2x_{i2}+\dots+w_dx_{id} + b = w^Tx_i+b，f(x_i) \approx y_i \]

目标

通常使用均方误差（mean square error，MSE）来衡量模型的预测值 \(f(x_i)\) 和真实值 \(y_i\) 之间差异的大小：

\[\text{MSE} = \sum_{i=1}^m(f(x_i)-y_i)^2 = \sum_{i=1}^m(y_i-wx_i+b) \]

我们希望 MSE 越小越好，所以我们需要找到一组参数 \(w\) 和 \(b\) 来最小化 MST。\(w\) 和 \(b\) 学到之后，模型就得以确定。

均方误差对应了几何中的欧式距离，基于均方误差最小化来进行模型求解的方法被称为最小二乘法（least square method）。在线性回归中，最小二乘法试图找到一条直线，使所有点到直线的欧式距离之和最小。

参数估计

求解 \(w，b\) 使得均方误差 \(E_{w,b}=\sum_{i=1}^m(y_i-wx_i+b)\) 最小的过程被称为线性回归模型的最小二乘参数估计（parameter estimation）。为了方便计算，我们将参数表示为向量的形式，令 \(\hat w = (w; b)\)，将数据集 \(D\) 表示为一个 \(m \times (d+1)\) 的矩阵，也就是 m 行 d+1 列，前 \(m \times d\) 列对应 m 个样本，最后一列全为 1，为了和 b 进行计算，也就是

将标记也表示为向量的形式 \(y = (y_1;y_2;\dots;y_m)\)，则均方误差 \(E_{\hat w}\) 可以写为：

\[E_{\hat w} = (y-X \hat w)^T(y-X \hat w) \]

为了求 \(E_{\hat w}\) 的最小值，可以求 \(E_{\hat w}\) 对 \(\hat w\) 的导数：

\[\frac{\partial E_{\hat w}}{\partial \hat w} = 2 X^T(X\hat w-y) \]

令上式为 0，如果 \((X^TX)\) 是满秩矩阵，就可以求得解析解 \(\hat w^{*} = (X^TX)^{-1}X^Ty\)，其中，\((X^TX)^{-1}\) 是 \((X^TX)\) 的逆矩阵。则最终求解的模型为：

\[f(x_i) = w^*x_i+b^* \]

上面公式的具体的求解步骤可以参考这里。

如果 \((X^TX)\) 不是满秩矩阵，例如样本的数量小于单个样本的属性数，则存在多个解析解，它们均能使均方误差最小化。具体选择哪个解析解，由算法的偏好决定，常见的做法是引入正则化（regularization）项：

• \(L_1\) 正则化：此时我们的目标是找到 \(\hat w\) 来最小化下式

\[(y-X \hat w)^T(y-X \hat w) + \lambda||\hat w||_1 \]

其中，\(\lambda>0\) 为正则化系数，调整正则化项与均方误差的比例。

• \(L_2\) 正则化：此时我们的目标是找到 \(\hat w\) 来最小化下式

\[(y-X \hat w)^T(y-X \hat w) + \lambda||\hat w||_2^2 \]

其中，\(\lambda>0\) 为正则化系数，调整正则化项与均方误差的比例。

• 同时引入 \(L_1\) 正则化和 \(L_2\) 正则化：此时我们的目标是找到 \(\hat w\) 来最小化下式

\[(y-X \hat w)^T(y-X \hat w) + \lambda \rho ||\hat w||_1 + \frac{\lambda(1-\rho)}{2}||\hat w||_2^2 \]

其中，\(\lambda>0\) 为正则化系数，调整正则化项与均方误差的比例；\(\rho \in [0,1]\) 用来控制 \(L_1\) 正则化和 \(L_2\) 正则化之间的比例。

对数线性回归

在线性回归中，我们的目标是找到模型 \(f(x_i)=w^Tx_i+b\)，使得 \(f(x_i)\) 尽可能地接近真实值 \(y_i\)。在对数线性回归中，我们的目标是找到模型 \(f(x_i)=w^Tx_i+b\)，使得 \(f(x_i)\) 尽可能地接近真实值 \(y_i\) 的对数 \(\ln y_i\)，其实也就是试图让 \(e^{w^Tx_i+b}\) 逼近 \(y_i\)：

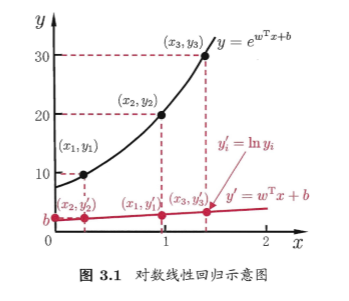
对数线性回归是输入空间到输出空间的非线性函数映射。更一般地，考虑单调可微函数 \(g(\cdot)\)，令

\[y_i = g^{-1}(w^Tx_i+b) \]

这样得到的模型称为广义线性模型，其中函数 \(g(\cdot)\) 被称为联系函数（link function）。对数回归函数就是广义线性模型在 \(g(\cdot)=ln(\cdot)\) 时的特例。

逻辑斯蒂回归

线性回归是用来求回归问题的，如果要求分类问题，例如二分类，\(y\in \{0, 1\}\)。我们需要将线性回归模型的输出连续值 \(z = w^Tx+b\) 转化为离散的 0/1 值。

一种方法是使用单位阶跃函数（unit-step function），如果 \(z>0\) 就判为正例，小于 0 就判为 反例，等于 0 可任意判别。如下图中红色线段表示的函数：

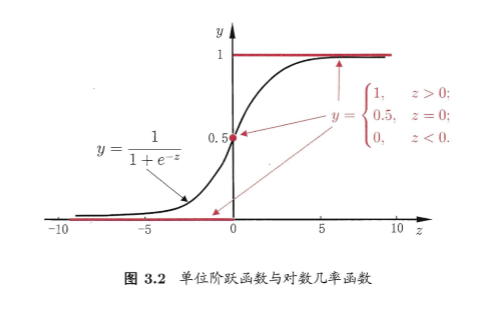
单位阶跃函数有一个缺点，就是它不连续，不能用作广义线性模型中的 \(g(\cdot)\)。于是，我们希望找到找到在一定程度上能近似单位阶跃函数的替代函数，并希望它单调可微。对数几率函数（logistic function）就是这样的一个常用的替代函数：

\[y = \frac{1}{1+e^{-z}} \]

对数几率函数的形状就是上面图 3.2 中的黑色曲线。对数几率函数是一个Sigmoid函数（S型函数），它将 \(z\) 转化为一个接近 0 或 1 的 y 值，并且在 z = 0 的附近变化很陡。将对数几率函数作为广义线性模型中的 \(g^{-1}(\cdot)\)，可以得到

\[y = \frac{1}{1+e^{-(w^Tx+b)}} = \frac{e^{w^Tx+b}}{1+e^{w^Tx+b}} \]

由上式可以得到

\[1-y = \frac{1}{1+e^{w^Tx+b}} \]

从而，有

\[\frac{y}{1-y} = e^{w^Tx+b} \]

两边取对数，有

\[\ln \frac{y}{1-y} = w^Tx+b \]

若将 \(y\) 视为 \(x\) 作为正例的可能性，则 \(1-y\) 就是 \(x\) 作为反例的可能性，两者的比值 \(\frac{y}{1-y}\) 称为几率（odds），反映了 \(x\) 作为正例的相对可能性。对几率取对数则得到对数几率（log odds，亦称logits） ：

\[\ln \frac{y}{1-y} \]

由此可以看到，我们实际上在寻找一个模型 \(f(x_i)=w^Tx_i+b\)，使得 \(f(x_i)\) 逼近真实标记的对数几率，所以这种方法对应的模型就叫做对数几率回归（logistic regression，logit regression），又称逻辑斯蒂回归。需要注意的是，虽然逻辑斯蒂回归名称中有“回归”二字，但它实际上是一种分类模型。

参数估计

令

\[P(y=1|x) = \pi(x) = \frac{1}{1+e^{-(w^Tx+b)}} = \frac{e^{w^Tx+b}}{1+e^{w^Tx+b}} \\ P(y=0|x) = 1-\pi(x) = \frac{1}{1+e^{w^Tx+b}} \]

我们可以通过** 极大似然法（maximum likelihood method）**来估计 \(w\) 和 \(b\)。在这里，似然函数

\[\prod_{i=1}^m [\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i} \]

为了计算方便，我们对似然函数取对数，得到对数似然函数 \(L(w)\)：

\[\begin{align} L(w) &= \sum_{i=1}^m(y_i\log\pi(x_i)+(1-y_i)\log(1-\pi(x_i))) \\ &= \sum_{i=1}^m(y_i\log\pi(x_i)+\log(1-\pi(x_i))-y_i\log(1-\pi(x_i))) \\ &= \sum_{i=1}^m(y_i \log \frac{\pi(x_i)}{1-\pi(x_i)}+log(1-\pi(x_i))) \\ &= \sum_{i=1}^m(y_i (w^Tx_i+b)-log(1+e^{w^Tx_i+b})) \\ &= \sum_{i=1}^m(y_i \beta^T \hat x_i - log(1+e^{\beta^T \hat x_i})) \\ \end{align} \]

其中，\(\beta = (w;b)，\hat x_i = (x_i; 1)\)，则 \(\beta^T \hat x_i = w^Tx_i + b\)。这样，问题就变成了以对数似然函数为目标函数的最优化问题（最大化），可以通过梯度下降法或者拟牛顿法等求解。最大化 \(L(w)\) 也就是最小化 \(L(\beta) = \sum_{i=1}^m(-y_i \beta^T \hat x_i + log(1+e^{\beta^T \hat x_i}))\). \(L(\beta)\) 对 \(\beta\) 的导数如下:

\[\begin{align} \frac{\partial{L(\beta)}}{\partial{\beta}} &= \sum_{i=1}^m(-y_i \hat x_i + \frac{\hat x_i e^{\beta^T \hat x_i}}{1+e^{\beta^T \hat x_i}}) \\ &= -\sum_{i=1}^m \hat x_i(y_i-\pi(\hat x_i)) \end{align} \]

所以，参数 \(\beta\) 的更新方式为：

\[\begin{align} \beta &= \beta - \alpha \frac{\partial{L(\beta)}}{\partial{\beta}} \\ &= \beta + \alpha(\sum_{i=1}^m \hat x_i(y_i-\pi(\hat x_i))) \end{align} \]

其实，也可以直接使用梯度上升来求 \(L(w)\) 的最大值，这样参数的更新方式是一样的。

参考

1、周志华《机器学习》
2、李航《统计学习方法》
3、http://www.huaxiaozhuan.com/统计学习/chapters/1_linear.html