【LeetCode-数学/二分查找】x 的平方根
题目描述
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例:
输入: 4
输出: 2
输入: 8
输出: 2
说明: 8 的平方根是 2.82842...,
由于返回类型是整数,小数部分将被舍去。
题目链接: https://leetcode-cn.com/problems/sqrtx/
思路1
在 1~x 范围内遍历,对于当前的数字 i:
- 如果 i == x / i (防溢出),则 i 就是 x 的平方根;
- 如果 i > x / i (防溢出),则 i-1 就是 x 的平方根;
代码如下:
class Solution {
public:
int mySqrt(int x) {
if(x==0) return 0;
for(int i=1; i<=x; i++){
if(i==x/i) return i; // 不能写成 if(i*i==x),会溢出
if(i>x/i) return i-1; // 不能写成 if(i*i>x),会溢出
}
return 0;
}
};
- 时间复杂度:O(sqrt(x))
- 空间复杂度:O(1)
思路2
上面的代码是顺序查找,可以写成二分查找加快速度。注意二分查找不能写成如下形式:
class Solution {
public:
int mySqrt(int x) {
if(x==0) return 0;
int left = 1, right = x;
while(left<=right){
int mid = left + (right-left)/2;
if(mid == x/mid) return mid;
else if(mid > x/mid){
right = mid-1;
}else if(mid < x/mid){
left = mid+1;
}
}
return 0;
}
};
这就是普通的二分查找,这样写有一个问题,就是只有对平方根原本就是整数的数才会返回正确的结果,例如,4 的平方根是 2,能返回正确的结果,而 8 的平方根是 2.82842,不能返回正确的结果。
稍微改一下判断条件就行:
class Solution {
public:
int mySqrt(int x) {
if (x == 0) return 0;
if (x < 4) return 1;
int left = 1;
int right = x / 2;
while (left <= right) {
int mid = left + (right - left) / 2;
if (mid == x / mid || mid < x / mid && mid + 1 > x / (mid + 1)) return mid; // 如果mid < x / mid && mid + 1 > x / (mid + 1),说明mid就是答案
else if (mid > x / mid) right = mid - 1;
else if (mid < x / mid) left = mid + 1;
}
return 0;
}
};
推荐上面的写法,符合经典二分查找的写法,容易理解。
用二分查找求解还有一种写法(不推荐,不太好理解),就是和普通的二分查找一样,循环结束时会得到 mid,如果 mid*mid = x,返回 mid;如果 mid*mid>x,返回 mid-1。代码如下:
class Solution {
public:
int mySqrt(int x) {
if(x==0) return 0;
int left = 1;
int right = x;
int mid = 1;
while(left<right){
mid = left + (right-left)/2;
if(mid==x/mid) break;
else if(mid<x/mid) left = mid+1;
else if(mid>x/mid) right = mid;
}
if(mid<=x/mid) return mid;
else return mid-1;
}
};
推荐这种写法,因为形式上和普通二分查找的写法一样,最后根据 mid 平方和 x 的情况返回即可。
这样写可以(二分查找的两种写法):
class Solution {
public:
int mySqrt(int x) {
if(x==0) return 0;
int left = 1;
int right = x;
int mid = 1;
while(left<=right){
mid = left + (right-left)/2;
if(mid<x/mid) left = mid+1;
else if(mid>x/mid) right = mid-1;
else break;
}
if(mid<=x/mid) return mid;
else return mid-1;
}
};
- 时间复杂度:O(logx)
- 空间复杂度:O(1)
思路3
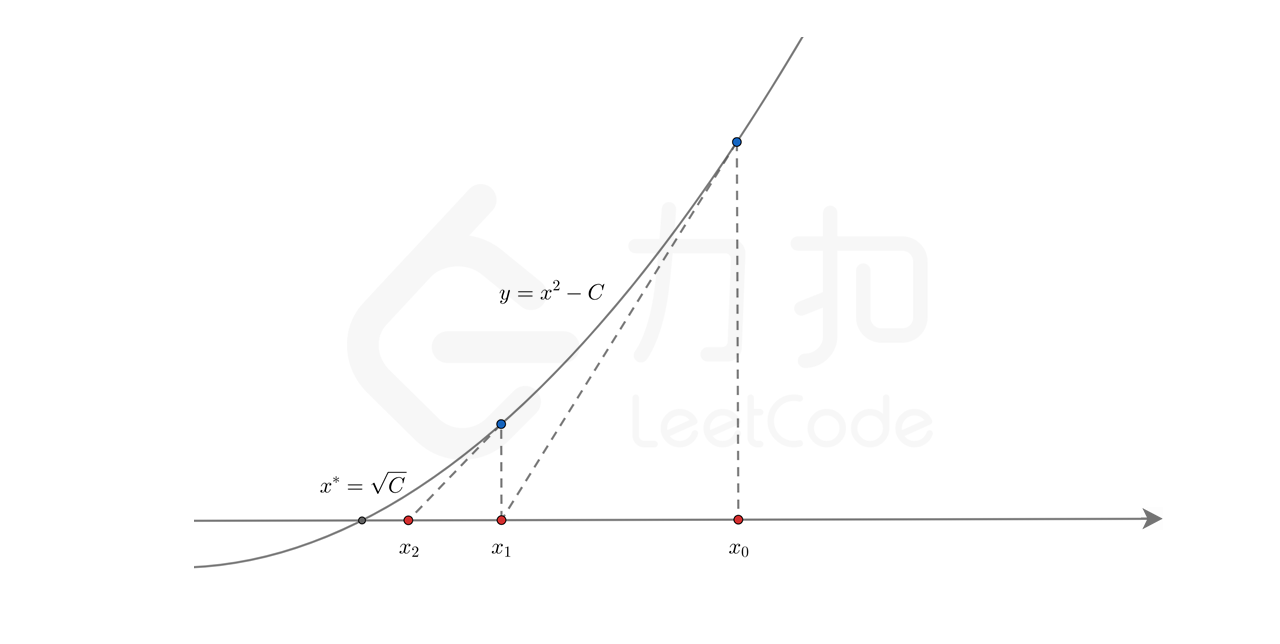
使用牛顿迭代法。牛顿迭代法是一种快速找函数零点的方法,求 C 的平方根就是找函数 f(x) = x^2 - C 的零点。牛顿迭代法的过程如下:
- 选择一个初始点(x0, f(x0)),以该点以及该点的斜率(2*x0)做一条切线,该切线与 x 轴的相交点为 (x1, 0);
- 以 x1 作垂线与函数 f(x) 的交点为 (x1, f(x1)),重复上面的步骤,我们就可以得到一个距离零点非常近的点。
下面计算 \(x_i\) 和 \(x_{i+1}\) 之间的关系,过点 \((x_{i}, f(x_{i}))\) 且斜率为 \(2x_i\) 的直线方程为
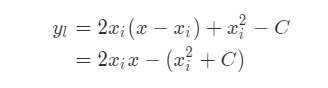
该直线与 x 轴的交点就是 \(x_{i+1}\)。令 y=0,得
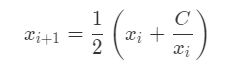
当 \(x_i\) 与 \(x_{i+1}\) 相差非常小时(例如相差 1e-6 或者 1e-7),我们就认为 \(int(x_i)\) 是零点,也就是我们要求的平方根。
代码如下:
class Solution {
public:
int mySqrt(int x) {
if(x==0) return 0;
double C = x, curX = x;
while(true){
double nextX = 0.5 * (curX + C/curX);
if(fabs(nextX - curX)<1e-7){
break;
}
curX = nextX;
}
return int(curX);
}
};
- 时间复杂度:O(logn)
- 空间复杂度:O(1)
思路4
使用数学的方法(被称为“袖珍计算器算法”):

需要注意的是,由于计算机无法存储精确的浮点数,所以这种方法求得的答案 ans 会有误差。例如,对于数字 2147395600,\(e^{\frac{1}{2}lnx}\)的结果 46639 与正确答案 46640 相差 \(10^{-11}\)。所以,我们求得 ans 后需要判断 ans 和 ans+1 哪一个才是正确的答案。代码如下:
class Solution {
public:
int mySqrt(int x) {
if(x==0) return 0;
int ans = exp(0.5 * log(x));
if((ans+1)<=x/(ans+1)) return ans+1;
else return ans;
}
};
- 时间复杂度:O(1)
- 空间复杂度:O(1)
参考
1、https://leetcode-cn.com/problems/sqrtx/solution/x-de-ping-fang-gen-by-leetcode-solution/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号