【LeetCode-树】验证二叉搜索树

题目描述

给定一个二叉树，判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。
  示例：

输入:
    2
   / \
  1   3
输出: true

输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

题目链接： https://leetcode-cn.com/problems/validate-binary-search-tree/

思路1

使用递归来做。根据二叉排序树的性质我们可以知道：当前节点的值是该节点左子树取值的上界并且是该节点右子树取值的下界。所以我们设计一个取值范围(lower, upper)来进行递归，当递归到某个节点时，我们进行如下判断：

• 如果当前节点为空，则返回true；
• 如果当前节点值val<=lower或者val>=upper，则返回false;

在递归的过程中更新lower和upper的值。递归过程如下图：

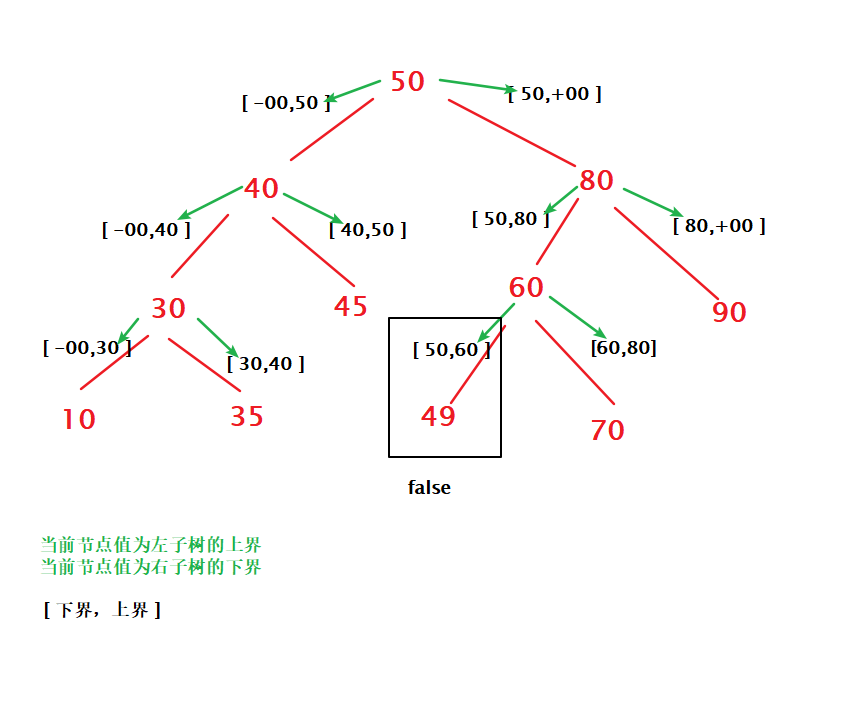
图来自这篇题解。
代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        if(root==nullptr) return true;
        if(root->left==nullptr && root->right==nullptr) return true;

        return judge(root, LONG_MIN, LONG_MAX); // 注意要用 long
    }

    bool judge(TreeNode* root, long left, long right){  // 注意要用 long
        if(root==nullptr) return true;

        if(root->val<=left || root->val>=right) return false;
        return judge(root->left, left, root->val) && judge(root->right, root->val, right);
    }
};

注意范围的初始化，因为测试数据中有比 int 最小值还小的数据，所以用 long 来初始化。

• 时间复杂度：O(n)
• 空间复杂度：O(h)
  h 为树的高度。

思路2

二叉搜索树的中序遍历是一个升序序列，所以我们可以对二叉搜索树进行中序遍历，在遍历的过程中判断当前节点是否大于上一个节点即可。代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:

    long long pre = LONG_MIN; // 初始化为比int最小值还小的数
    bool isValidBST(TreeNode* root) {
        if(root==nullptr) return true;

        if(!isValidBST(root->left)) return false;   // 判断左子树是不是二叉排序树
        if(root->val<=pre) return false;
        pre = root->val;    // 更新pre值为根节点
        return isValidBST(root->right); // 判断右子树是不是二叉排序树
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(h)